首先想一个问题：计算机需要怎样才能理解词语？在人类世界里，我们能轻易理解"国王"和"女王"的关系，就像"男人"和"女人"的关系一样。但计算机如何"理解"这种微妙的语言关系呢？答案是：将词语转换成数字，也就是词向量（Word Vector）。现在带你了解目前最经典的词向量模型——Word2Vec，并探讨其核心技术中一个非常关键的工程优化问题：Softmax 加速。

一、从"词语"到"向量"：词向量的演进

在计算机能够处理语言之前，我们首先需要一种方式来表示词语。

1. 最初的尝试：One-Hot 编码

最简单直接的想法是给每个词一个独一无二的编号。假设我们的词典里只有四个词：【猫，狗，国王，女王】。

我们可以这样表示：

• 猫：[1, 0, 0, 0]
• 狗：[0, 1, 0, 0]
• 国王：[0, 0, 1, 0]
• 女王：[0, 0, 0, 1]

这种方法叫做 One-Hot 编码。它简单，但有两个致命缺陷：

1. 维度灾难：如果词典有10万个词，那每个词的向量就是10万维，而且其中只有一个1，其他全是0，非常稀疏，计算效率低下。
2. 语义鸿沟：从向量上看，任意两个词之间的距离都是一样的。计算机无法知道"猫"和"狗"是近义词，而"猫"和"国王"关系不大。

2. 革命性的思想：分布式表示 (Word Embedding)

为了解决 One-Hot 的问题，研究者们提出了一种新的表示方法：词嵌入（Word Embedding），也叫分布式表示。

它不再使用稀疏的、长长的向量，而是用一个稠密的、低维的向量来表示一个词。比如，我们可以用一个100维的向量来表示一个词。

例如：

• 猫：[0.1, -0.5, 1.2, …, 0.8]
• 狗：[0.2, -0.4, 1.0, …, 0.7]
• 国王：[0.9, 0.8, -0.1, …, -0.3]
• 女王：[0.8, 0.9, -0.2, …, -0.2]

在这个向量空间里，意思相近的词，它们的向量也更接近。更神奇的是，向量之间可能存在着有趣的代数关系，比如著名的： vector('国王') - vector('男人') + vector('女人') ≈ vector('女王')

这说明词向量真正捕捉到了词语之间的语义信息！而 Word2Vec 就是生成这种神奇词向量的经典模型。

二、Word2Vec：让词语拥有"生命"

Word2Vec 不是一个单一的模型，而是一个工具集，包含两种主要的学习算法：CBOW 和 Skip-gram。它们都基于一个核心思想，即**" distributional hypothesis “（分布式假说）**：一个词的意义，由它周围的词来决定。

1. CBOW (Continuous Bag-of-Words) 模型：看上下文猜中心词

CBOW 的任务是：根据一个词的上下文（周围的词），来预测这个词本身。

• 举个例子：对于句子 “the quick brown fox ___ over the lazy dog”，我们挖掉 “jumps” 这个词，让模型去预测它。
• 训练过程：
  1. 取出上下文词 “the”, “quick”, “brown”, “fox”, “over”, “the”, “lazy”, “dog” 的词向量。
  2. 将这些词向量相加并取平均，得到一个综合的上下文向量 h。
  3. 使用一个简单的神经网络，以 h 为输入，去预测中心词 “jumps”。

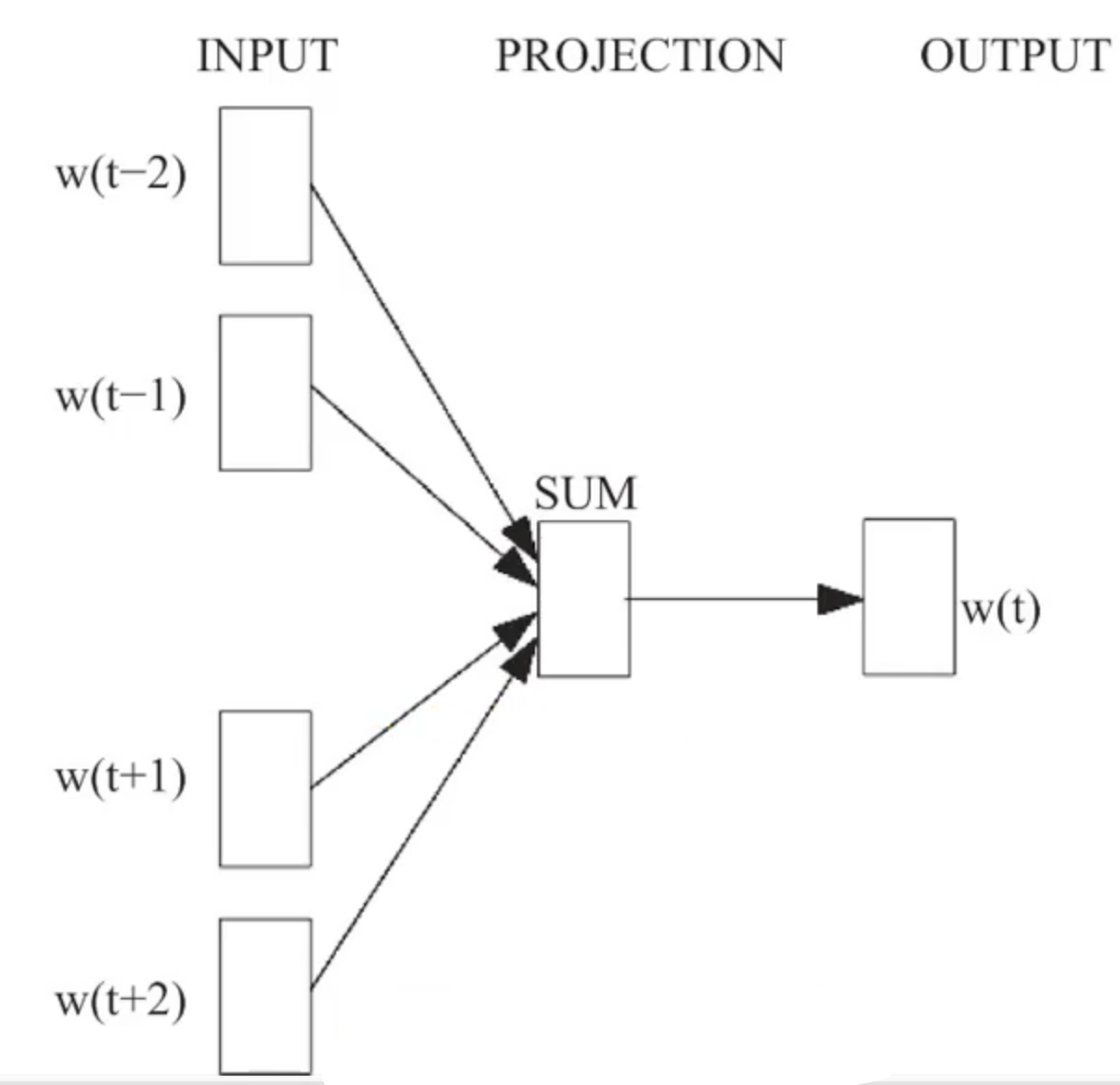
用公式简单表达就是： $$h=\frac{1}{2c}\sum_{i=1}^{2c}w_i$$ 其中 w_i 是上下文词的向量，2c 是上下文窗口的大小。然后通过一个分类器（比如 Softmax）来预测目标词： $$p(y_j|context(y_j))=softmax(W’h)$$ W' 是一个权重矩阵，y_j 是我们预测的中心词。模型的目标就是让这个概率最大化。

2. Skip-gram 模型：看中心词猜上下文

Skip-gram 的任务正好和 CBOW 相反：根据一个中心词，来预测它周围的词。

• 举个例子：还是上面的句子，我们给模型 “jumps” 这个词，让它来预测 “the”, “quick”, “brown”, “fox” 等上下文。
• 训练过程：
  1. 输入中心词 “jumps” 的词向量 w_t。
  2. 使用一个神经网络，以 w_t 为输入，分别预测它周围的每一个上下文词。

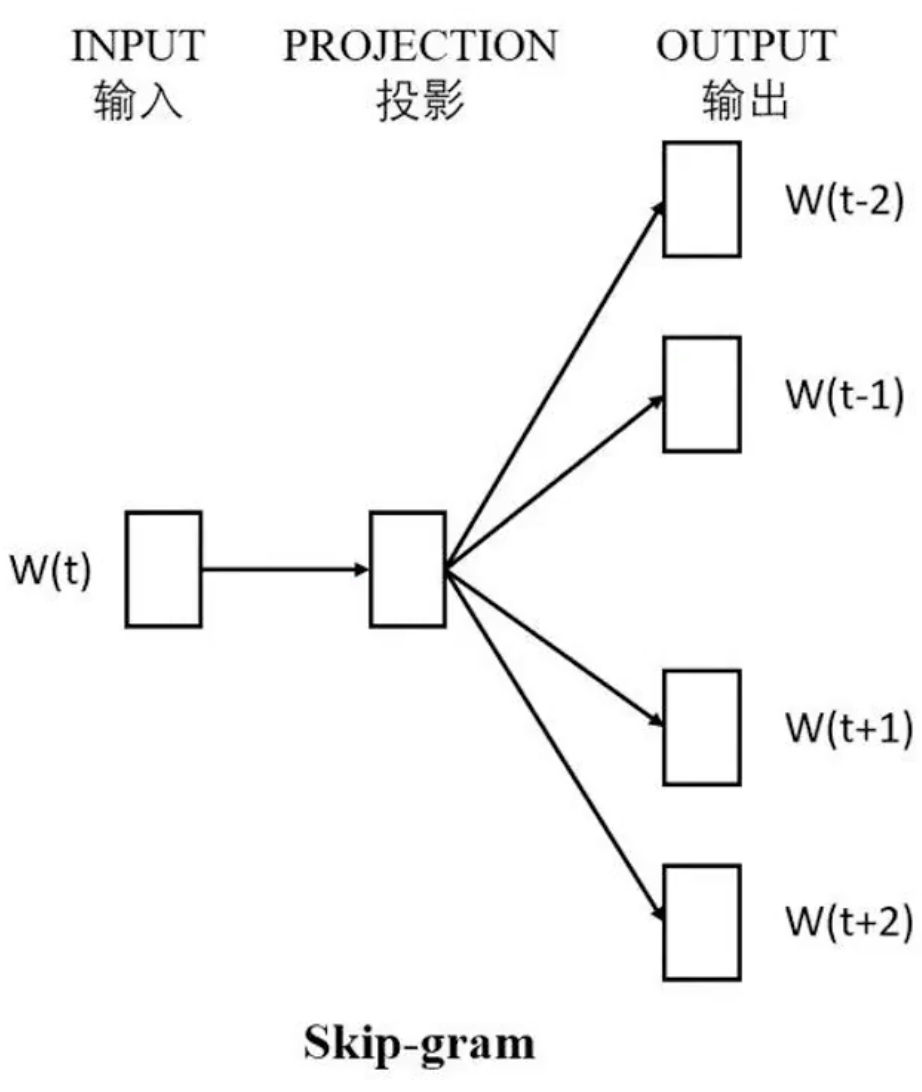
用公式表达： $$p(context(x_t)|x_t) = \prod_{w_j \in context(x_t)} p(w_j|w_t)$$ 模型的目标是最大化整个上下文的联合概率。

3. CBOW vs. Skip-gram: 怎么选？

• Skip-gram: 对低频词效果更好，在大型语料库中表现更优越。
• CBOW: 训练速度比 Skip-gram 快几倍，对于高频词有更好的表示。

在实际应用中，Skip-gram 更为常用，因为它能产出更高质量的词向量。

三、Softmax 的困境与加速技巧

在 Word2Vec 的训练过程中，无论是 CBOW 还是 Skip-gram，最后一步都需要一个分类器来从整个词典中（可能有几十万个词）选出概率最大的那个词。这个分类器通常就是 Softmax。

Softmax 的公式如下： $$p(y_j|context) = \frac{\exp(score(y_j, context))}{\sum_{i=1}^{V}\exp(score(y_i, context))}$$

这里的 V 是词典的大小。问题就出在分母上：为了计算一个词的概率，我们需要计算所有 V 个词的分数，然后求和。当 V 非常大时（例如百万级别），这个计算量是惊人的，会使得模型训练变得异常缓慢。

为了解决这个问题，研究者们提出了两种非常聪明的近似方法：Hierarchical Softmax 和 Negative Sampling。

1. Hierarchical Softmax (层级 Softmax)

核心思想：将一个巨大的"V选1"的多分类问题，变成一系列"二选一"的二分类问题。

它是如何做到的呢？通过构建一棵霍夫曼树 (Huffman Tree)。

• 霍夫曼树：一种特殊的二叉树，它会根据词频来构建。词频越高的词，其在树中的路径就越短。树的每个叶子节点代表一个词，从根节点到每个叶子节点都有一条唯一的路径。

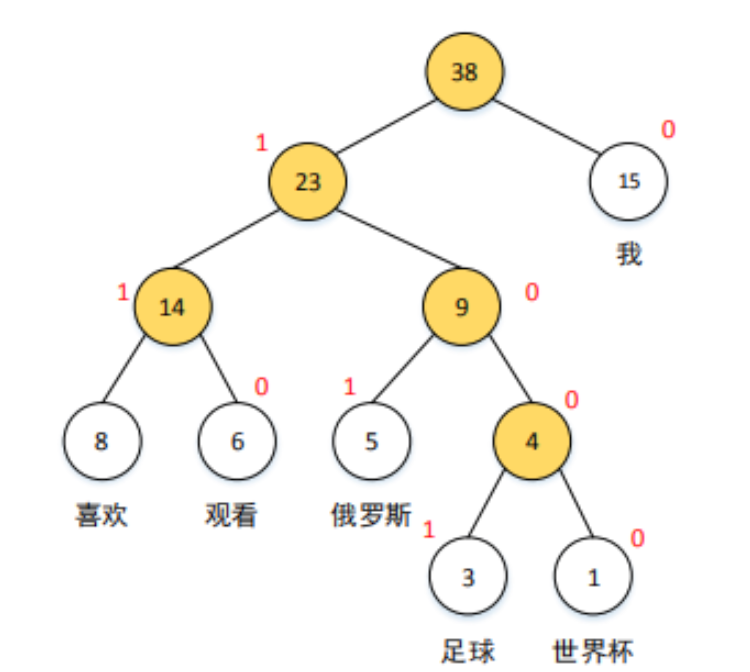
计算过程：

1. 我们不再直接计算某个词的概率。
2. 而是计算从根节点出发，经过一系列向左或向右的选择，最终到达该词所在叶子节点的路径概率。
3. 在树的每一个非叶子节点，我们都训练一个简单的二分类器（逻辑回归，使用 Sigmoid 函数），来判断应该向左走还是向右走。
4. 最终，目标词的概率就等于这条路径上所有二分类概率的连乘。

比如上图中，要计算"足球"的概率，我们需要计算： P(向右) * P(向左) * P(向左) * P(向右)

这样一来，原本需要计算 V 次的运算，现在只需要计算 log₂(V) 次（树的高度），计算量大大降低！

2. Negative Sampling (负采样)

核心思想：既然完整计算分母代价太大，我们干脆就不算了，用一种近似的方法来代替。

做法： 负采样将问题从"预测正确的词"转换成"区分正确的词和错误的词”。

在训练时，对于一个给定的 (中心词, 上下文词) 对，比如 (fox, quick)，我们知道这是一个正样本 (positive sample)，因为它们确实一起出现过。

然后，我们再从词典中随机挑选出几个（比如 k=5 个）不相关的词，如 “car”, “apple”, “sky” 等，将它们与中心词 “fox” 组合成负样本 (negative samples)，如 (fox, car), (fox, apple) 等。

接下来，模型的目标就变成了：

• 对于正样本，预测其为"真"的概率尽可能高（接近1）。
• 对于负样本，预测其为"真"的概率尽可能低（接近0）。

负采样的数学原理

那么，这个"区分真假"的目标是如何用数学公式来表示和优化的呢？

1. 定义概率：我们把问题看作一个逻辑回归。对于一个词对 (w, c)（w 是中心词，c 是上下文词），我们希望模型能判断它是不是正样本。我们用 D 来表示这个标签，D=1 为正样本，D=0 为负样本。

   • 一个词对是正样本的概率，我们用 Sigmoid 函数来定义： $$P(D=1|w, c) = \sigma(v_c^T v_w) = \frac{1}{1+e^{-v_c^T v_w}}$$ 这里 v_w 和 v_c 分别是中心词和上下文词的向量。我们希望这个概率接近1。
   • 相应地，一个词对是负样本的概率就是： $$P(D=0|w, c) = 1 - P(D=1|w, c) = \sigma(-v_c^T v_w)$$ 我们希望这个概率也接近1。

2. 构建损失函数：对于一个正样本 (w, c_pos) 和 k 个负样本 (w, c_{neg,1}), ..., (w, c_{neg,k})，我们希望最大化下面这个联合概率： $$ \text{maximize} \quad \sigma(v_{c_{pos}}^T v_w) \prod_{i=1}^{k} \sigma(-v_{c_{neg,i}}^T v_w) $$ 这个公式的含义是：我们希望正样本的概率（第一项）和所有负样本的"非真"概率（连乘项）都尽可能大。

3. 最终的损失函数：在机器学习中，我们通常不是最大化一个目标，而是最小化一个损失函数 (Loss Function)。标准的做法是取上面目标函数的负对数（negative log-likelihood）： $$ L = - \log \left( \sigma(v_{c_{pos}}^T v_w) \prod_{i=1}^{k} \sigma(-v_{c_{neg,i}}^T v_w) \right) $$ $$ L = - \left( \log \sigma(v_{c_{pos}}^T v_w) + \sum_{i=1}^{k} \log \sigma(-v_{c_{neg,i}}^T v_w) \right) $$ 这就是我们在训练时需要最小化的目标。通过梯度下降等优化算法，模型会不断调整词向量 v，使得正样本对的向量点积越来越大，而负样本对的向量点积越来越小，从而实现了"区分真假"的目标。

这相当于把一个巨大的多分类问题，变成了一系列小的二分类问题。我们只需要更新正样本和少数几个负样本的权重，而不用去管词典里其他几十万个词，效率极高。

如何选择负样本？ 如果完全随机采样，会倾向于选到高频词。Word2Vec 的作者提出了一种巧妙的带权采样方法，使得低频词也有一定的机会被选中。

四、这些加速技巧现在还香吗？

一个自然的问题是：在今天 GPU 算力如此强大的背景下，这些花哨的加速技巧还有用武之地吗？

• 对于词向量训练：在很多场景下，如果词典规模不是特别夸张（比如几万到几十万），现代硬件已经可以直接硬扛全量 Softmax 的计算。因此，在一些最新的语言模型库中，这些技巧可能不再是默认选项。
• 但思想永存：
  1. 当输出空间巨大时：想象一下人脸识别，输出空间是全世界几十亿人；或者在推荐系统中，推荐的商品可能有几千万种。在这种场景下，全量 Softmax 是绝对不可行的，类似负采样的思想就变得至关重要。
  2. 树形结构的重要性：层级 Softmax 所利用的树形结构，是计算机科学中解决"大海捞针"问题的经典方法，其思想在数据库索引、搜索等领域无处不在。

总结

• 词向量是将词语数值化的关键技术，它能捕捉词语的语义信息。
• Word2Vec 是生成高质量词向量的经典模型，包含 CBOW（上下文预测中心词）和 Skip-gram（中心词预测上下文）两种方法。
• Softmax 在词典很大时计算开销巨大，是性能瓶颈。
• Hierarchical Softmax 和 Negative Sampling 是两种有效的加速策略，它们将大问题化解为小问题，是算法优化思想的绝佳体现。