这次依旧是通过线性变换来了解逆矩阵、列空间、秩和零空间的概念。注意其中并不会讨论计算方法。首先我们能体会到了用矩阵来描述对空间的线性变换，线性代数不但在计算机图形学和机器人学中非常有用，还能帮助我们求解线性方程组，那就先从恒等变换和线性方程组的关系开始吧！

线性方程组与矩阵向量乘法

线性方程组是各个方程关于未知量均为一次的方程组：

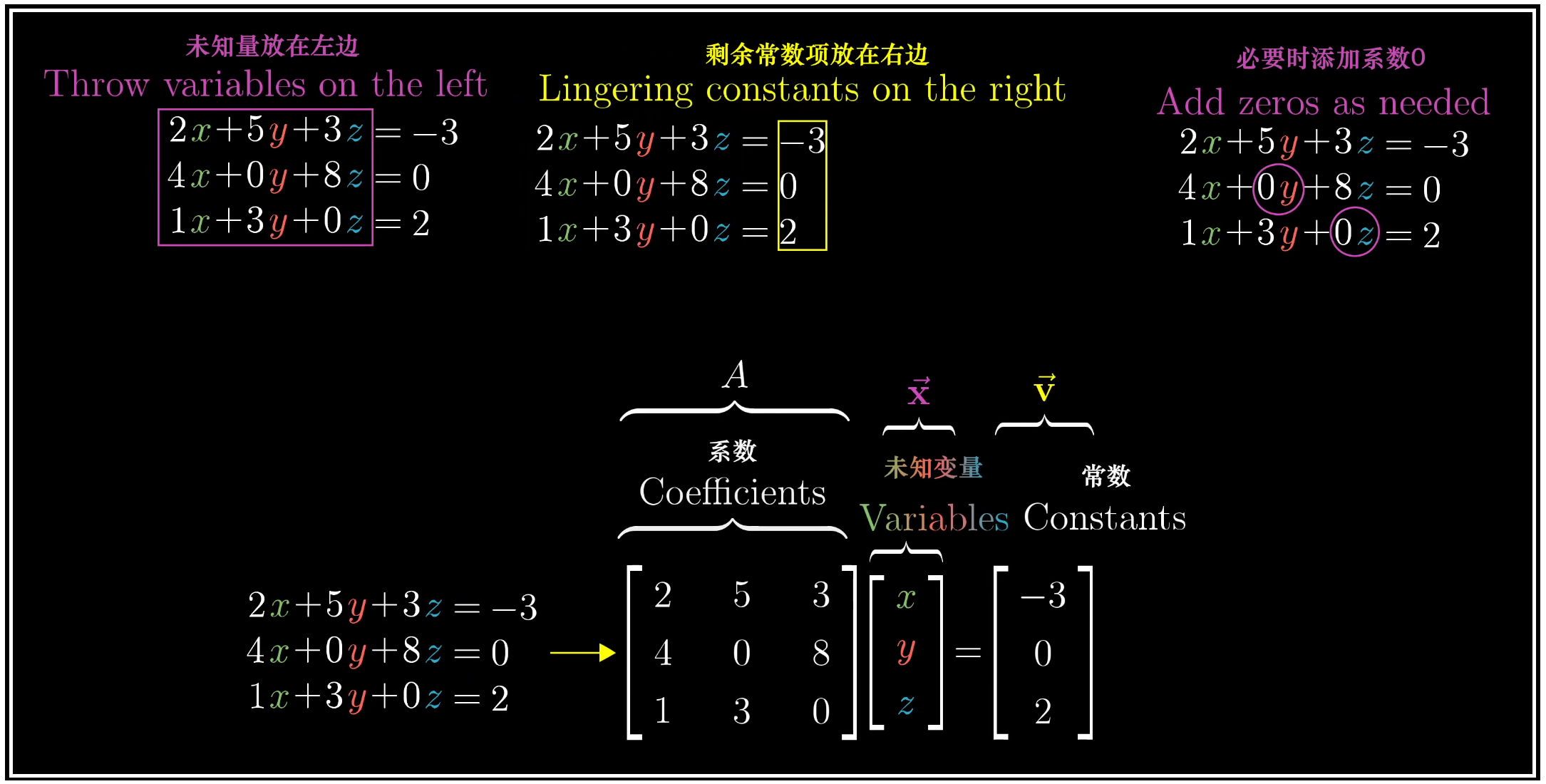
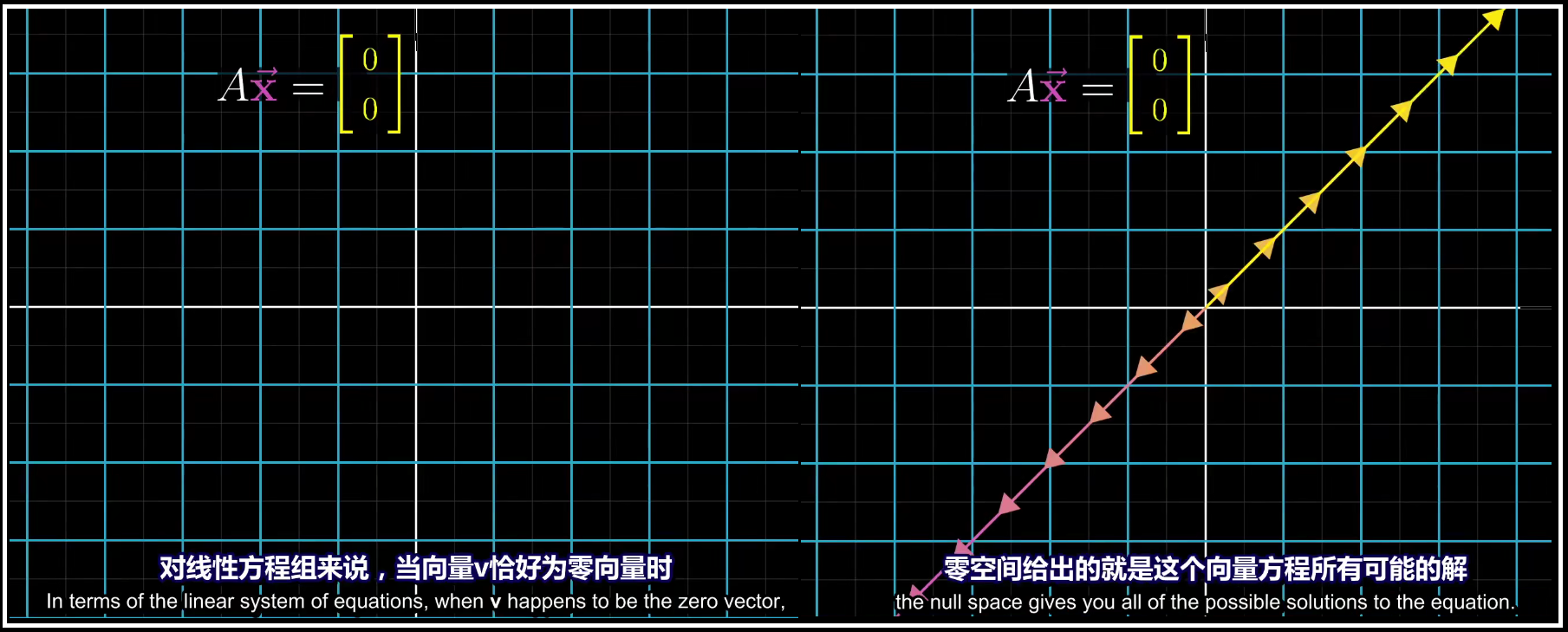
如下上图所示，对于一个线性方程组，我们可以看成是一个未知变量，也就是上面的 $\vec{x}$ ，被一个矩阵做线性变换，然后得到一个新的向量 $\vec{v}$ ，我们需要求解得出的就是原来的向量。

注意，这不仅仅只是将方程组写进一行的书写技巧，还阐述了这个问题中最优美的几何直观部分。整个求解方程组的过程尽然就是寻找原本传入的向量，即 $A\vec{x} = \vec{v}$，$A$ 和 $\vec{v}$ 都是已知的，求解出 $\vec{x}$ 即可。

逆矩阵的本质——逆变换

还记得行列式得意义吗？ 行列式的几何意义：矩阵所对应的线性变换改变面积（体积）的比例。 当矩阵行列式为0，说明它将原空间线性变换后压缩为一条线或一个点（二维情况下），即使原空间维度降低。这也解释了为何矩阵列向量线性相关时，经过它的线性变换后，原空间发生维度衰减。它的行列式为0。

$det(A) \neq 0$

如果矩阵 A 的行列式不为0，说明空间并不会被挤压为零面积的区域，此时有且仅有一个向量在变换后与 $\vec{v}$ 重合，我们可以通过逆变换来找到这个向量：

也就是如同倒带一样，如果一个变换是逆时针旋转90°，那么它的逆变换就是顺时针旋转90°，此时顺时针旋转90°的矩阵就称为逆时针旋转90°的逆矩阵，记为 $A^{-1}$

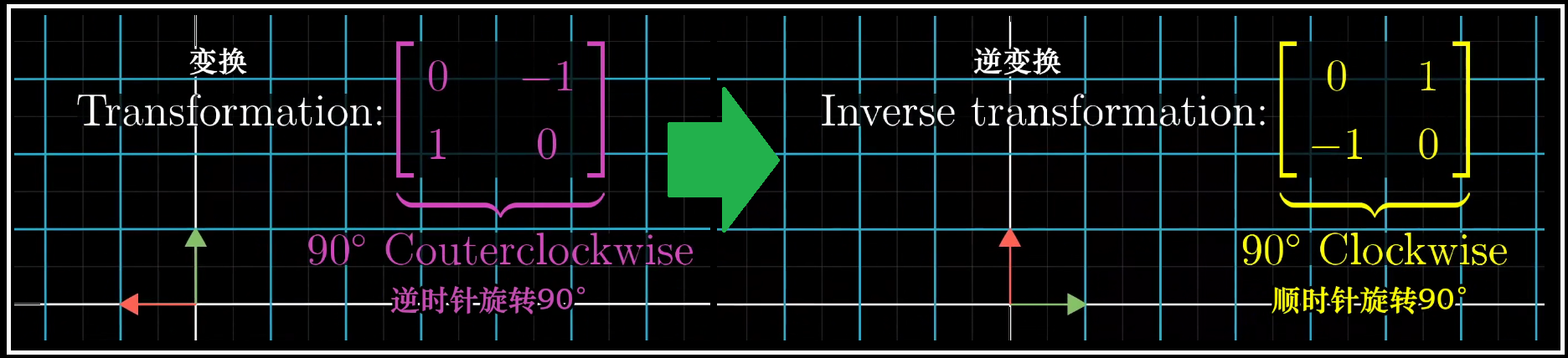
总之， $A^{-1}$ 是满足以下性质的唯一变换：首先应用 $A$ 所代表的变换，再应用 $A^{-1}$ 所代表的变换，就会回到原始状态，两个变换相继作用在代数上体现为矩阵乘法，所以 $A^{-1}$ 的核心性质在于 $A^{-1}$ 乘以 $A$ 等于一个"什么都不做"的矩阵。这种"什么都不做"的变换被称为"恒等变换"。所以给矩阵两边都乘以 $A^{-1}$ ，就可以求解向量方程。

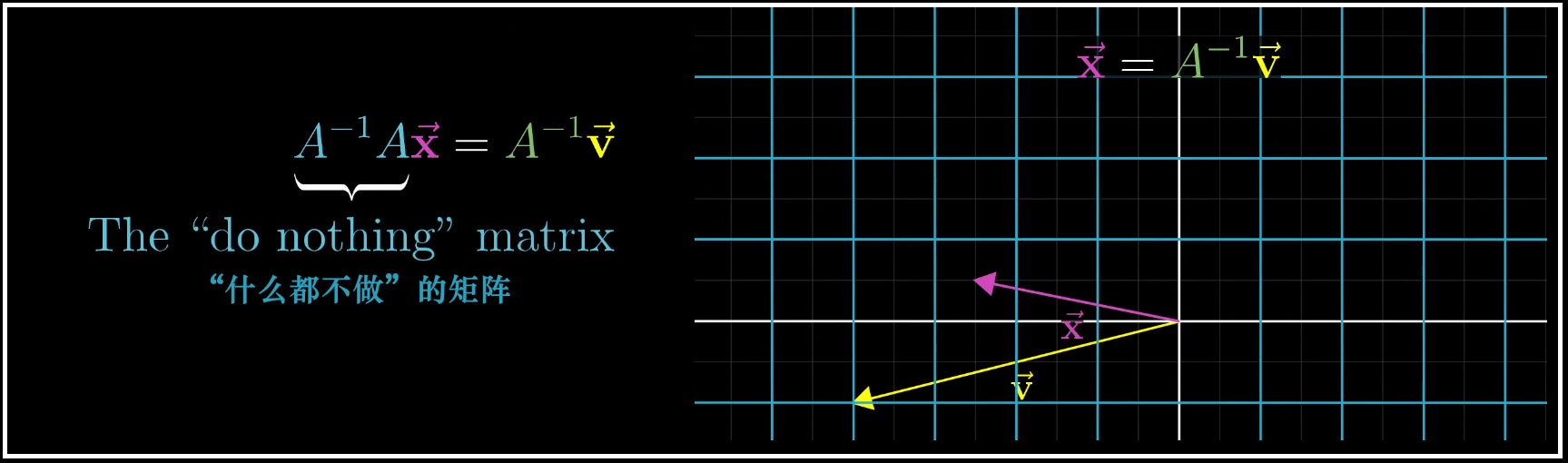
在高维几何直观下其实也非容易理解，依旧是 $A\vec{x} = \vec{v}$，然后两便同时乘以 $A^{-1}$ ，就等于左边什么都没做，恢复到了初始状态。

如此看来，如果 $det(A) \neq 0$，那么必定存在 $A^{-1}$， 使得应用 $A$ 所代表的变换，再应用 $A^{-1}$ 所代表的变换，就会回到原始状态。此时想要求解方程，只需要将$A^{-1}$与 $\vec{v}$ 相乘即可。

$det(A) = 0$

如果矩阵 A 的行列式为0，与这个方程组相关的变换将空间压缩到更低的维度，此时没有逆变换，正如你不能将一条直线 “解压缩” 成一个平面，至少这不是一个函数能完成的事情。如果变换将三维空间压缩为一个平面、一条直线、甚至是一个点，那么它也没有逆变换，它们都对应着行列式为0的情况，此时所有区域都被压缩到零体积。

即使不存在逆变换，解仍有可能存在，比如一个变换把空间压缩为一条直线，且向量 $\vec{v}$ 正好处于这条直线上。如果一个三维空间被压缩成一条直线时，那么与平面相比，解存在的难度就更高了，虽然它们的行列式都是0。

是不是觉得如果仅仅用行列式来描述一个变换太单一了呢？

其实除了零行列式之外，我们也可以用 “秩” 来描述这个变换，当变换的结果是一条直线的时候，也就是说结果是唯一的，则这个变换的秩就为1，如果变换后的向量落在某个二维平面上，则这个变换的秩就为2，所以：秩代表了变换后空间的维度。对于2×2的矩阵，它的秩最大为2；但是对于3×3的矩阵来说，秩为2意味着空间被压缩了，只不过没有秩为1的时候压缩的那么严重，如果秩为3，则表示变换后基向量张成的空间仍然是三维空间。

列空间、零空间

所有可能的输出向量 $A\vec{v}$ 构成的集合就是矩阵A的列空间。矩阵的列表示基向量变换后的位置，这些变换后的基向量张成的空间就是所有可能的变换结果。所以列空间就是矩阵的列所张成的空间。

所以秩的更精确的定义就是列空间的维数！

当秩达到最大值的时候，则秩与列数相等，此矩阵是满秩矩阵。

注意，零向量一定在列空间中，因为线性变换的原则就是原点位置保持不变。对于满秩矩阵来说，唯一能在变换后还保持在原点的就是零向量自身：

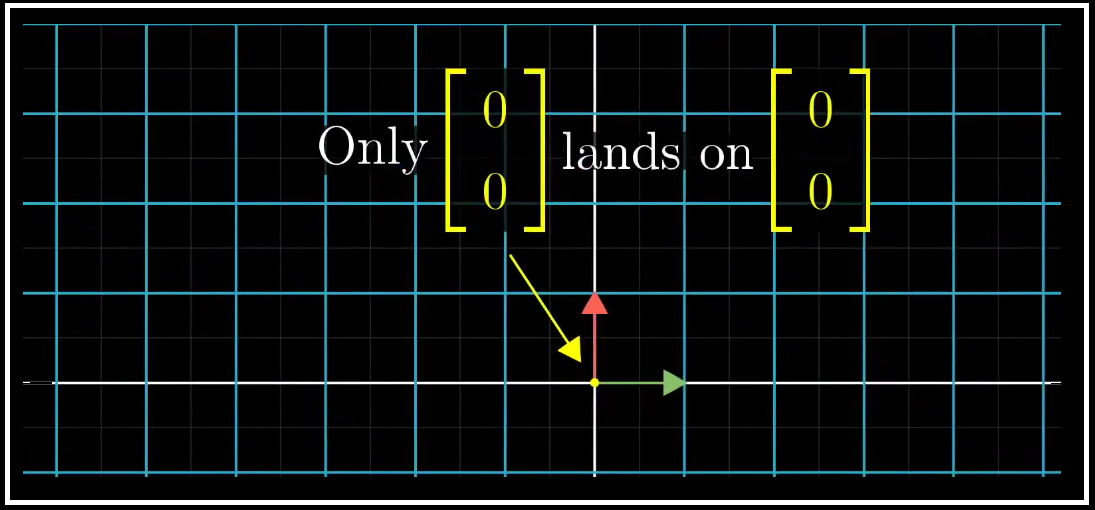
变换后落在原点的向量的集合被称为该矩阵的 “零空间” 或者 “核”