本篇文章中引用了3Blue1Brown视频中的截图，也是线性代数系列的第一个小总结：理解什么是向量，向量的线性组合，什么是向量张成的空间，向量的线性相关性如何理解。最近更新线性代数的系列文章，强烈推荐 bilibili 上一位叫做 3Blue1Brown 的Up主，讲了很多数学方面的内容，而且讲述的角度非常独特，真正可以让人感觉到数学的魅力。

向量的加法与数乘

线性代数围绕两种基本运算，向量加法与向量数乘。

有三种不同的观点来看待向量。分别以物理、计算机、数学的视角来看待向量。

物理：具有大小和方向的箭头；

计算机：向量是有序的数字列表；

数学：结合物理和计算机两种观点，向量可以是任何数，只要符合加法和乘法的定义。

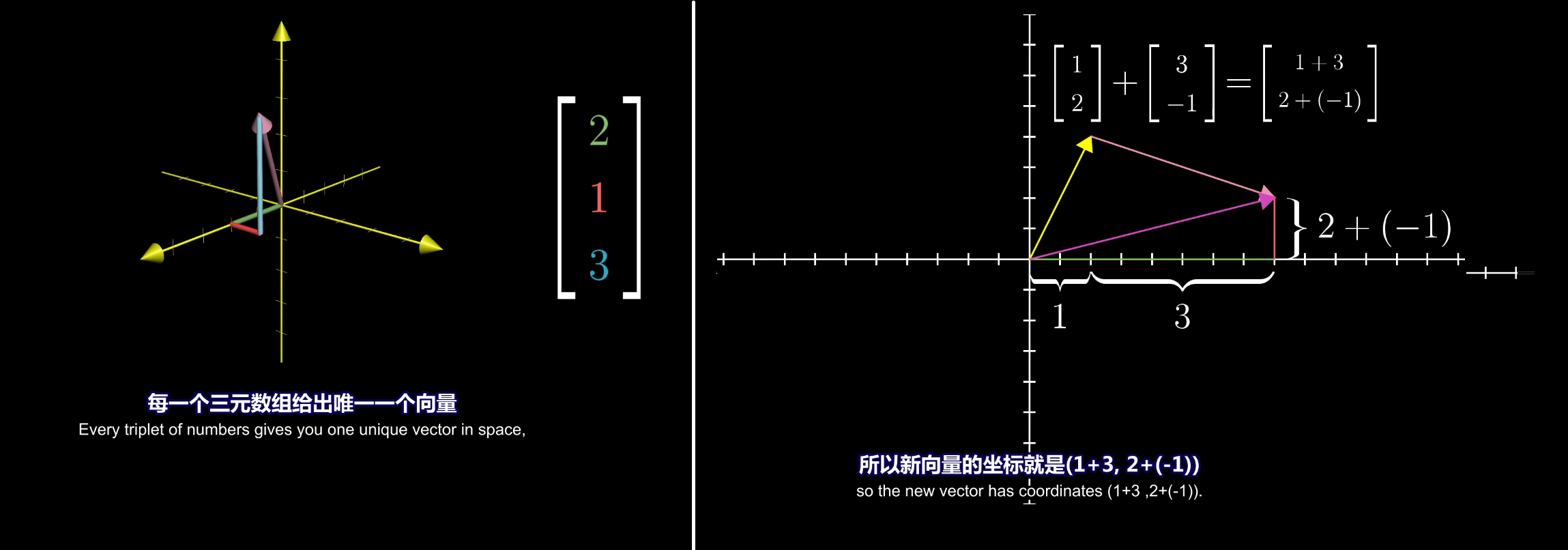
向量之所以要竖着写，是为了和点坐标相区别，向量可以看成一个起始点在坐标原点的带有方向的线段。

向量的加法c=a+b可以看成一个动态运动的过程，先走到a，在以a的结尾开始走b，最终从原点到b的终点就是c。

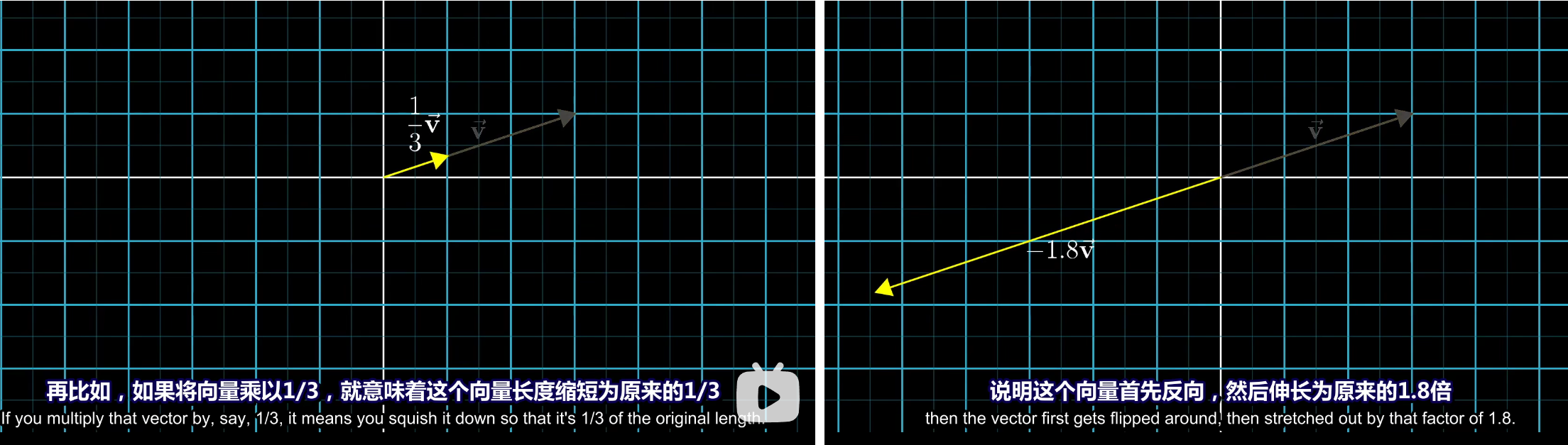
向量的乘法可以理解成缩放。

基向量、向量线性组合

基：向量空间的一组基是由张成该空间的一个线性无关的向量集；

当我们用数字描述向量时，它都依赖于我们正在使用的基。比如对于一个二维向量，当我们描述一个二维向量的时候是我们在基的基础上进行描述，比如当我们使用[1, 2] 来描述一个二维向量的时候，其实本质是1倍的i基向量, 2倍的 j 基向量所形成的向量。

正常情况下我们觉得，i 基向量对于迎着X轴的一个长度单元，，j 基向量对于迎着Y轴的一个长度单元。但是如果随便定一个i 基向量 和 j 基向量会发生什么呢？

张成的空间

如果固定其中一个向量，任意变化另一个向量，那么会得到一条直线。如果同时变化两个向量，那么会形成的一个二维平面，此平面所有的点表示的向量都可以由初始的两个基向量通过 线性组合 的方式得到。不过这里有一个特殊情况，那就是两个基向量都在同一直线：

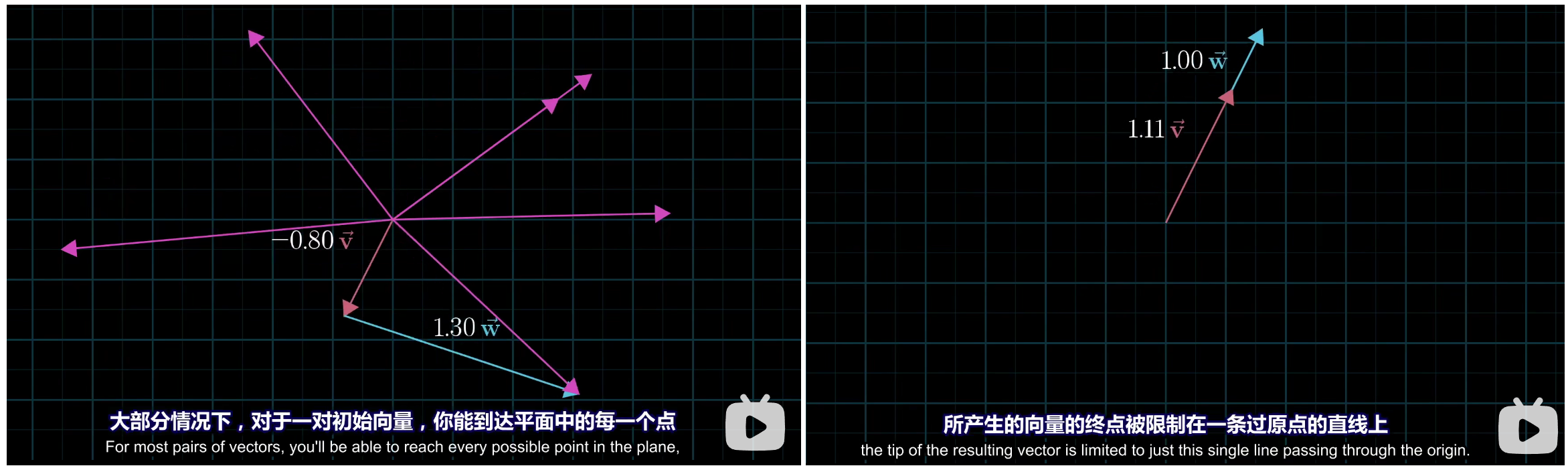
其实还有另一种情况，那就是两个基向量都是0向量的时候，无论怎么做线性组合，都只能待在原点！

张成的空间：所有可以表示为给定向量线性组合的向量的集合被称为给定向量张成的空间。 也就是上图中v向量与w向量全部线性组合的集合；

如果v向量与w向量都是0向量：其张成的空间就是一个点，就是原点！

如果v向量与w向量位于同一条直线：其张成的空间是一条直线！

如果v向量与w向量方向不一致：其张成的空间就是一个二维平面！

所以两个向量张成的空间实际上就是在问：仅仅通过向量加法和向量数乘这两种基础的运算，你能得到的所有可能的向量集合是什么？

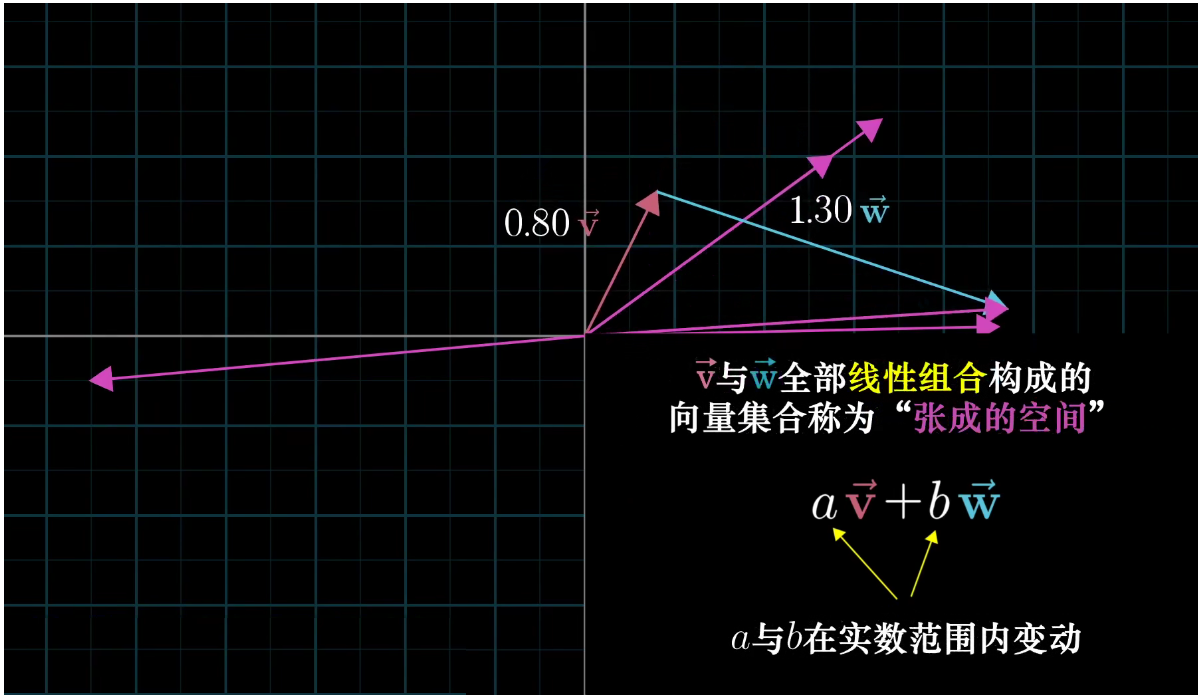
将向量的维度扩展到三维，那么两个向量张成的空间是什么样呢？

现在加入第三个向量，如果这第三个向量恰好落在前两个向量张成的平面上，无论怎么做线性组合，所张成的空间依旧是这个二维平面，张成的空间并没有发生改变。但是如果选择第三个向量没有落在前两个向量张成的平面上，则张成的空间会是整个三维空间：

线性相关与线性无关

前面提到的第三个向量恰好落在前两个向量张成的平面上的情况，还有两个向量共线的情况，都是其中至少有一组向量是多余的，即不会对张成的空间做出任何贡献，去掉其中一个向量也不会减少张成的空间，那么就认为这组向量是线性相关的，否则就是线性无关的：

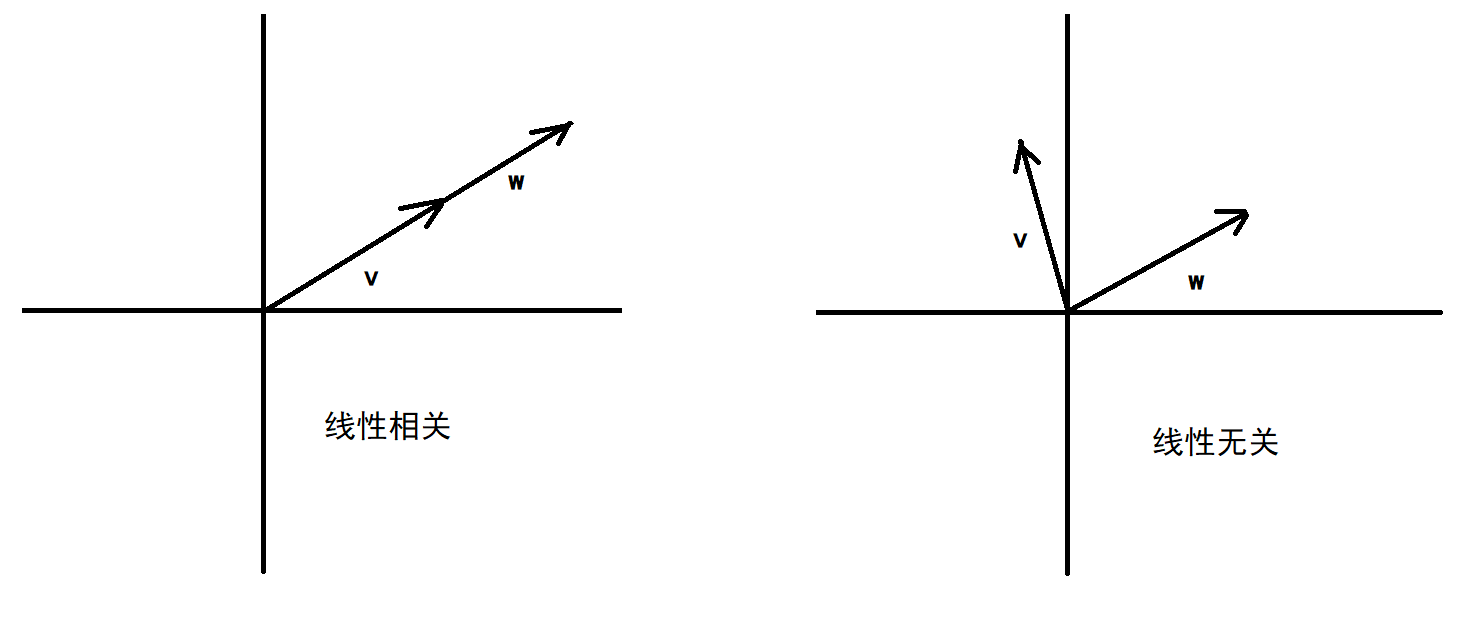
通过上面的学习，可以理解下面的话了：

向量空间的一组基是张成该空间的一个线性无关向量集合！