本次主要学习抗锯齿 SSAA 及 MSAA 算法和遮挡剔除 Z-Buffer 算法。

当我们把场景中的三角形光栅化显示到屏幕像素上时，会出现锯齿效果，其实很好理解，根据之前学习过的光栅化的流程，之前主要解决的是通过采样确定一个像素在不在这个三角形中的问题，现在要解决的就是锯齿问题。这类问题通常也叫做抗锯齿处理或者反走样（Antialiasing）。

反走样原理与算法

信号与采样 & 傅里叶变换

信号本质上就是一个函数，输入参数，输出结果。对于任何周期函数 $f(x)$ ，都有两种表现形式：时域、频域。其中我们最常见的便是时域的形式，也是现实世界的直观形式，可以理解成即 $f(x)$ 本身，把 x 当成时间，那么时域便是分析函数值关于时间 x 的关系。

而傅里叶告诉我们，任意一个周期函数 $f(x)$ 可以由若干个频率不同、振幅不同的余弦函数相加而成。

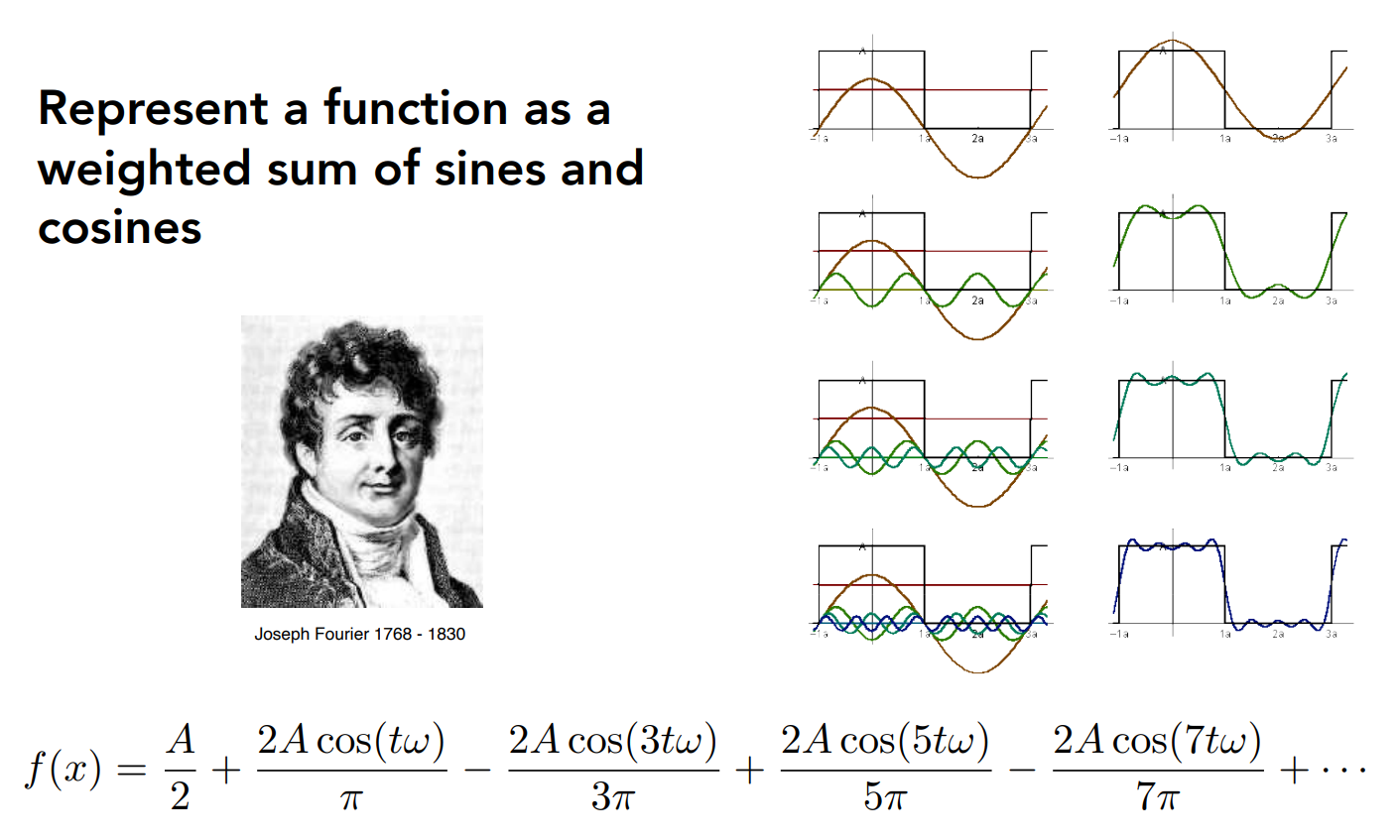
通过傅里叶变换，我们可以把时域信号变换为频域信号，反之通过傅里叶逆变换可以把信号从频域转为时域信号： $$ F(\omega)=\int_{-\infty}^{\infty} f(x) e^{-2 \pi i \omega x} d x $$ 傅里叶逆变换： $$ f(x)=\int_{-\infty}^{\infty} F(\omega) e^{2 \pi i \omega x} d \omega\

e^{i x}=\cos x+i \sin x $$ 当我们每隔一定间隔采样 $ f(x)$ ，实际上就是每隔一定间隔，分别采样这些组成信号的余弦波并相加起来。可以看到，低频余弦波的采样结果与实际余弦函数差别并不大，但是随着频率越来越高，余弦波的采样失真越来越严重：

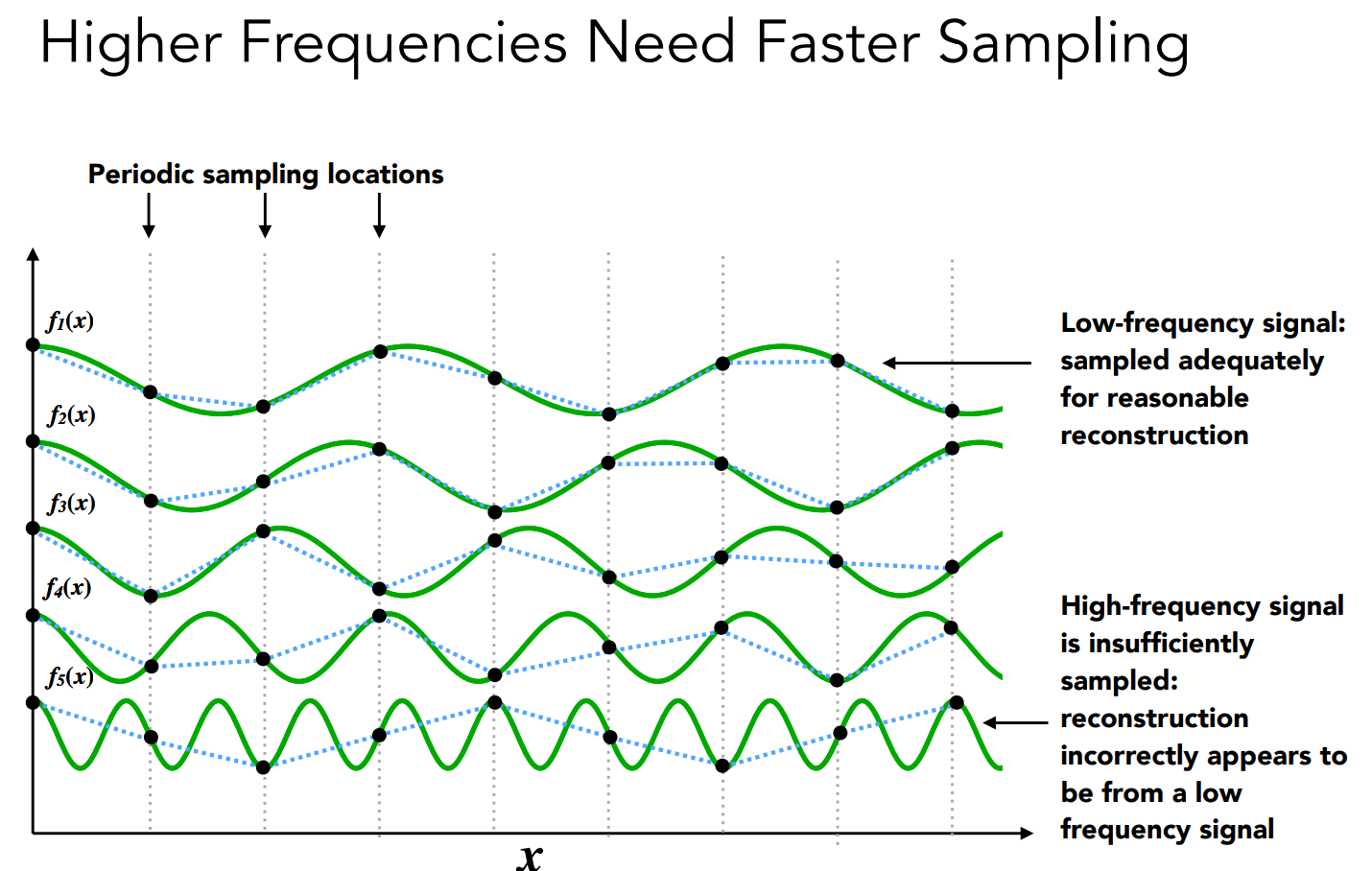
高频信号采样不足就被误认为是低频信号，在给定的采样中无法区分的两个频率，欠采样会产生频率混叠，比如下面的高频余弦波，本该是剧烈起伏的，采样的结果却是平缓起伏，与实际结果已经严重不一致：

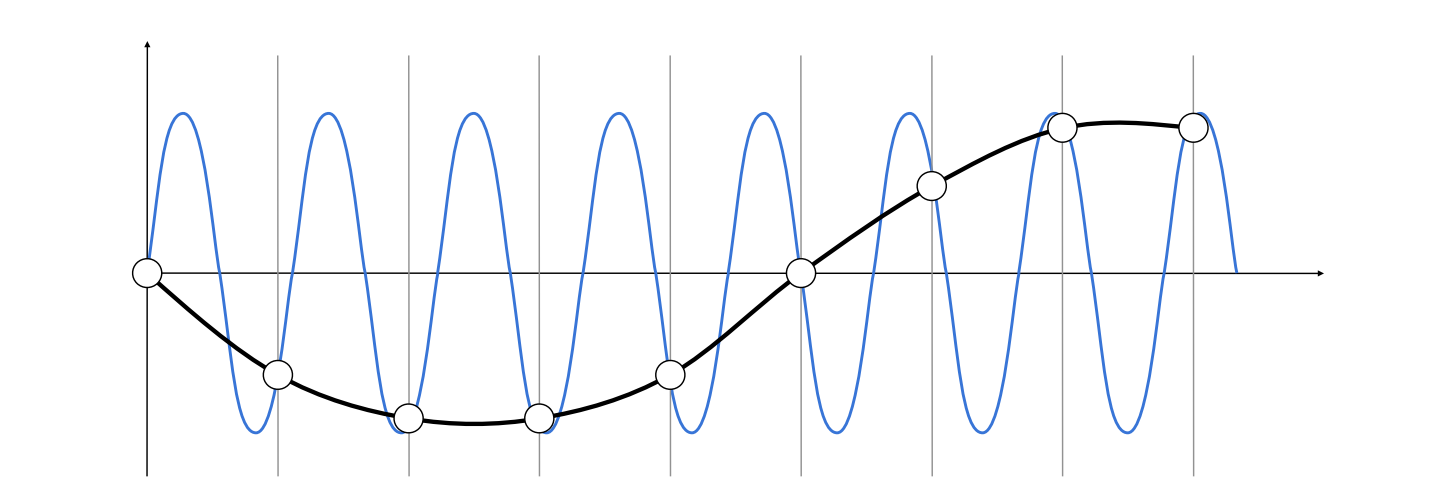
因此，当采样频率过低（采样间隔过大）时，信号中的高频信息会失真，这也是走样问题的来源。反走样要做的就是尽可能让高频信息量减少（高频余弦波的振幅减少）。

那么，对于目标采样频率（目标分辨率）的反走样基本原理为：

1、先把原始图片当成一种信号，即信号 $f(x)$ 输入一个二维位置 x，输出一个像素颜色值（那么自然而然，这张图片也可以由若干个不同频率的余弦波组成）

2、接下来，对时域函数（图片信号）进行卷积操作（即模糊图片），卷积操作实际上就是每个点取周围（包括点本身）的平均值。

容易想象得出到，经过卷积后的时域函数 $f (x)$ 会变得更加平缓（图片变得更加模糊）。这样分离出来的高频余弦波振幅更加小，换句话说，相当于我们把高频信息砍掉了，所以这就是一种低通滤波器。

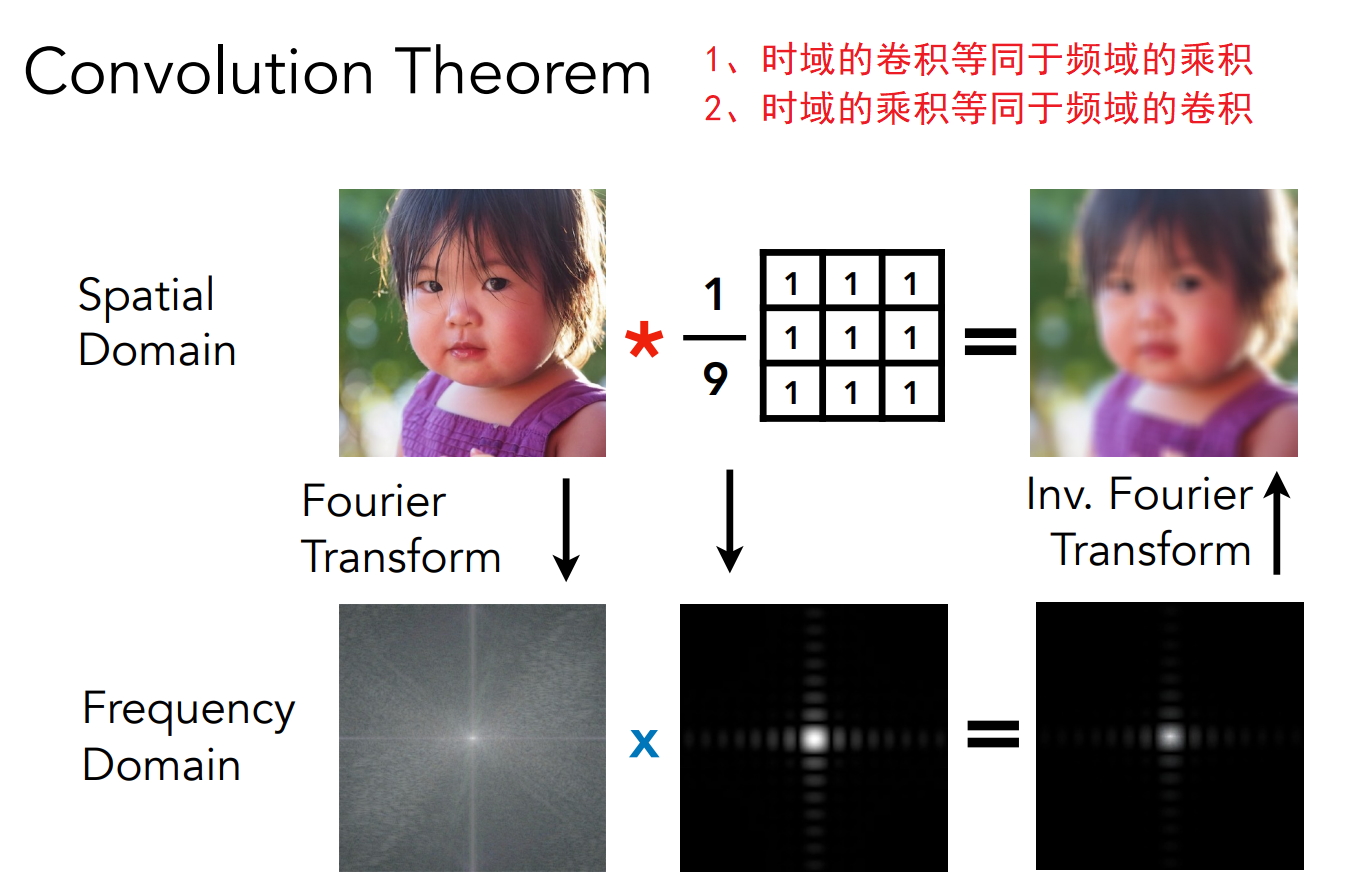
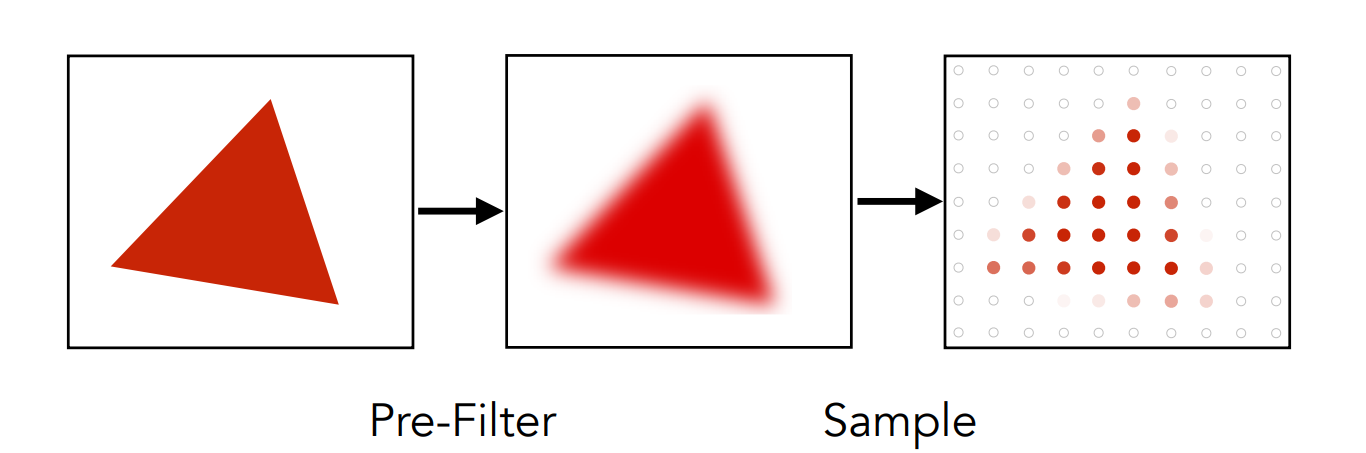
3、最后对这张卷积后的图片进行目标频率的采样，就能得到走样现象不明显的目标分辨率图片。

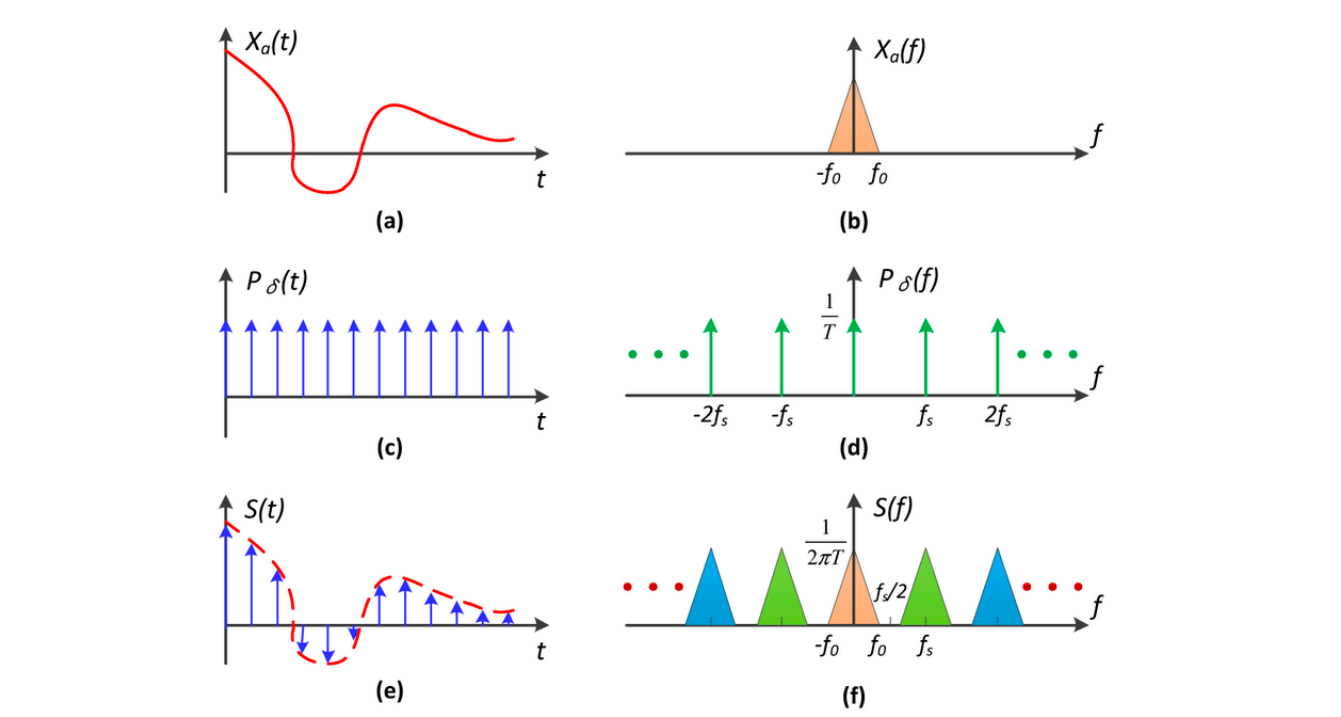
时域的离散化对应频域的周期化，下图中，c 作为一个一个的冲激函数乘以原函数 a 得到 e ，相当于把连续的函数给离散化了，对应到频域上是卷积操作，a、c 的频谱b和d做卷积，就得到了结果 f，其实就是把原函数的频谱 b 复制粘贴了很多份，然后经过一些过程将其转化为离散时间序列：

超采样抗锯齿 SSAA

超采样反走样 (Super Sampling Anti-Aliasing) ，如果有限离散像素点逼近结果不好，那么我们用更多的采样点去逼近不就会得到更好的结果了吗？所以根据这个思想我们可以把原来的每个像素点进行细分，比如下例中，我们将每个像素点细分成了4个采样点：

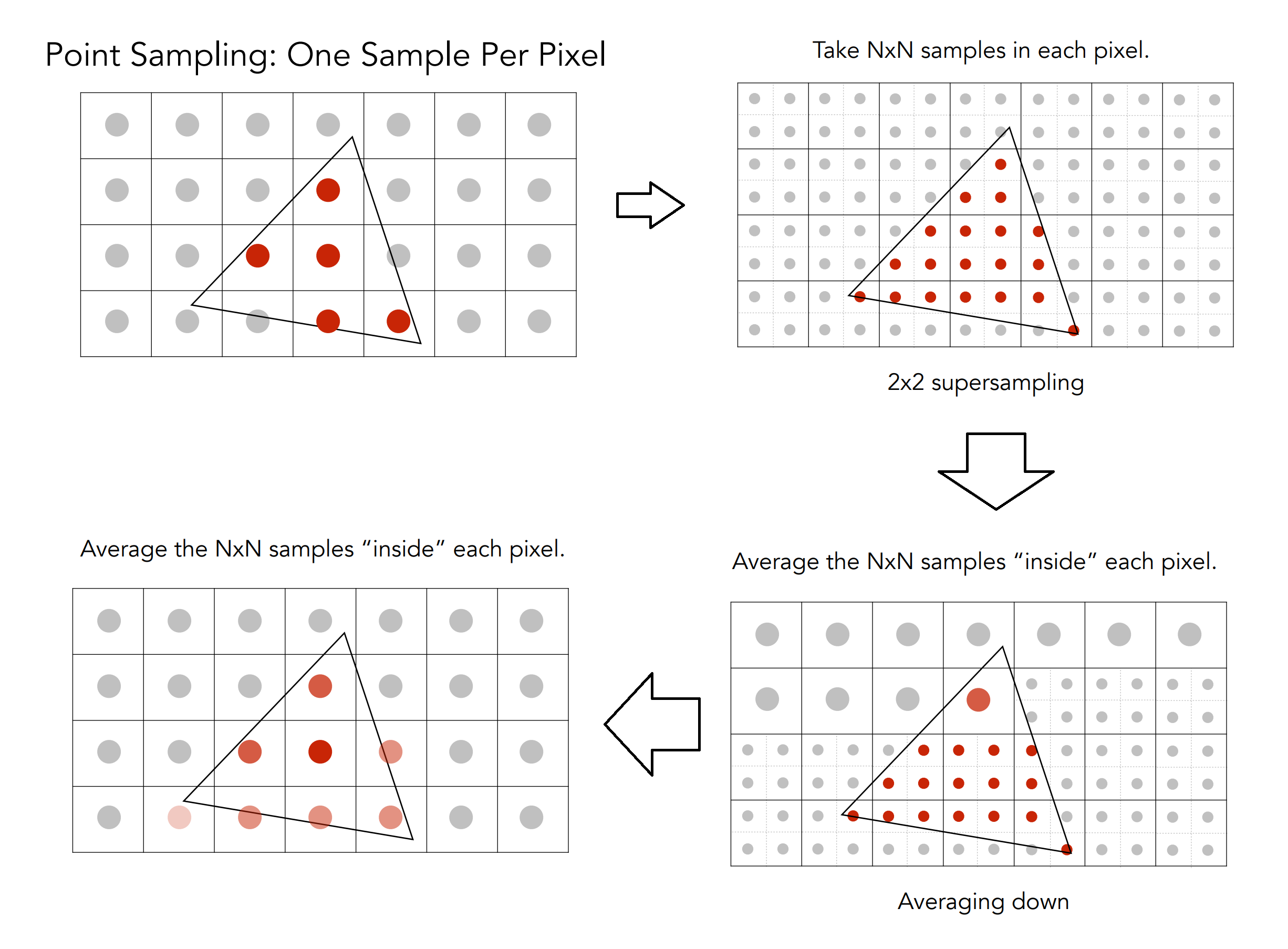
这就相当于原本一个像素只采样一次，现在我们采样4次，采样率直接提高至4倍。针对每一个子采样点，重复母像素的流程，判定是否在三角形内、深度检测、着色，最后每个子采样点都会得到各自的颜色，母像素的颜色就是子采样点颜色的平均。

从上图中可以看到，相当于将一个像素细化为四个采样点，此处的四个采样点分布有序且均匀，此类超采样称之为 OGSS(Ordered Grid Super-Sampling)。有研究者发现 OGSS 对于竖直和横向方向的超采样表现不太好（考虑到很多边缘都是竖直或者横向的），于是将四个采样旋转一个角度，得到 RGSS(Rotated Grid Super-Sampling)，下图比较了 OGSS 与 RGSS 的表现：

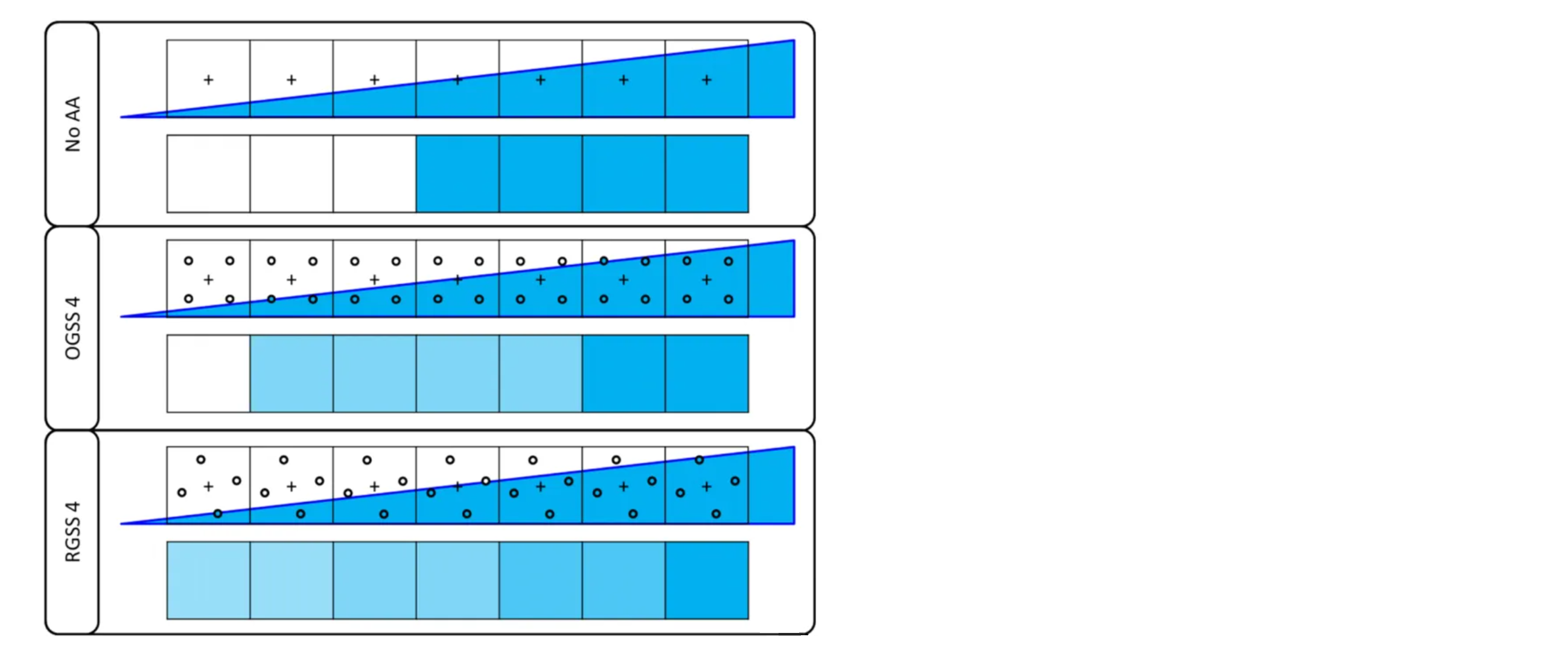
将4个子采样点的颜色平均后，三角形边缘的有些像素点会变淡，从宏观上看，锯齿就不那么明显了：

将图形先渲染到一张较大的贴图上，再将图形缩小。这种方式产生的额外的性能消耗比较大，因此一般很少会在实践中使用这种抗锯齿方式。移动设备上的 GPU，会使用 Tiled 模式的方式进行渲染。在 Tiled 模式下，屏幕会划分成 16x16的 tile，每个 tile 作为一个组进行渲染。在渲染每个 tile 时，FrameBuffer 会存储在 on-chip 缓存中，以便快速访问。当整个 tile 渲染完成后，on-chip 缓存中的 FrameBuffer 会写回到内存中，这样可以降低带宽的占用。 这类设备上使用 MSAA 时，就可以在 MSAA 的 FrameBuffer 写回内存时，进行 Resolve 操作，这样可以节省内存和带宽。在这类设备上使用 MSAA 时，就可以在 MSAA 的 FrameBuffer 写回内存时，进行 Resolve 操作，这样可以节省内存和带宽。

多重采样抗锯齿 MSAA

MSAA其实是对SSAA的一个改进，显然SSAA的计算量是非常大的，每个像素点分成4个采样点，我们就要进行4次的shading来计算颜色，额外多了4倍的计算量，如何降低它呢？

MSAA的做法也很容易理解，我们依然同样会分采样点，但是只会去计算究竟有几个采样点会被三角形覆盖， 相比 SSAA，MSAA 的优势是把采样点的深度、遮挡和光照计算分开，减少光照计算量。SSAA 是对每一个采样点都计算一次深度、遮挡和光照，最后才进行滤波解析，而 MSAA 只对每一个采样点计算深度、遮挡等，然后就滤波解析，最后对一个像素内的多个采样点只计算一次光照。

下图对比了两者的区别：

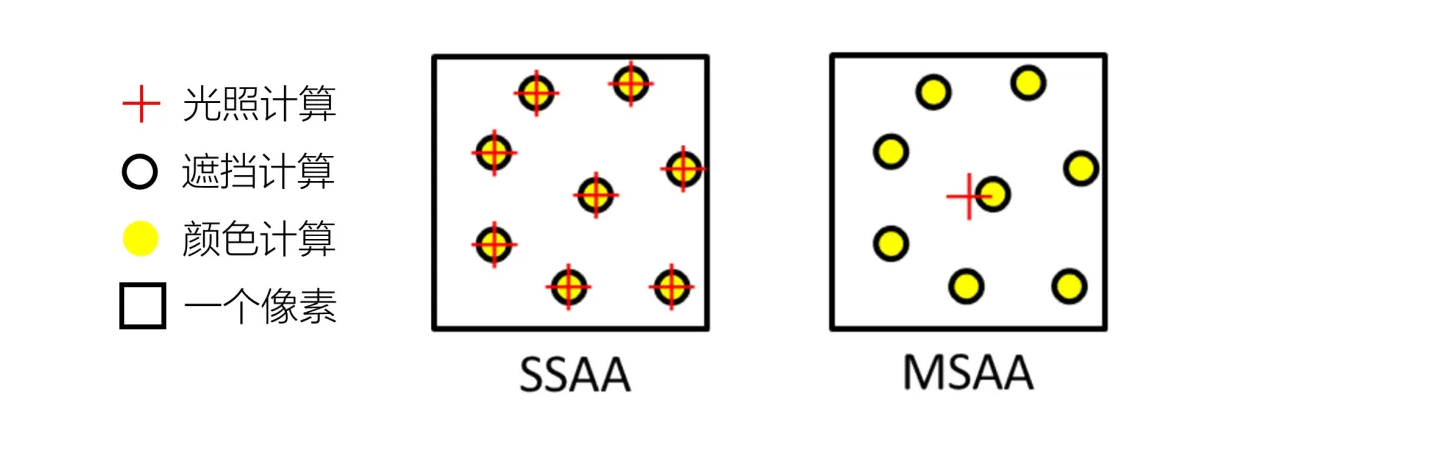
MSAA 相比 SSAA 少了很多的光照计算，所以速度提升不少，是使用最普遍的一种抗锯齿技术。

此处 MSAA 对一个像素计算一次光照的时候，选取的是像素的中心点，当然也可以对此点进行偏移，分别称之为 Center Sampling 和 Centroid Sampling，后者的效果更好但计算量更大，关于两者的区别可参考 GLSL: Center or Centroid? (Or When Shaders Attack!) ，此处不展开。

MSAA 虽然相比 SSAA 提高了性能，但是存储占用与 SSAA 相同，CSAA 则进一步改进了这一点。CSAA 是 NVIDIA 提出的，其主要思想是：进一步减少每个采样点的信息量。回顾前面：SSAA 是对每一个采样点计算深度、遮挡、颜色和光照，然后解析。MSAA 是对每一个采样点计算深度、遮挡、颜色，先解析，然后一个像素只计算一次光照，CSAA 与 MSAA 的区别在于，进一步减少计算颜色的采样点，如下图所示：

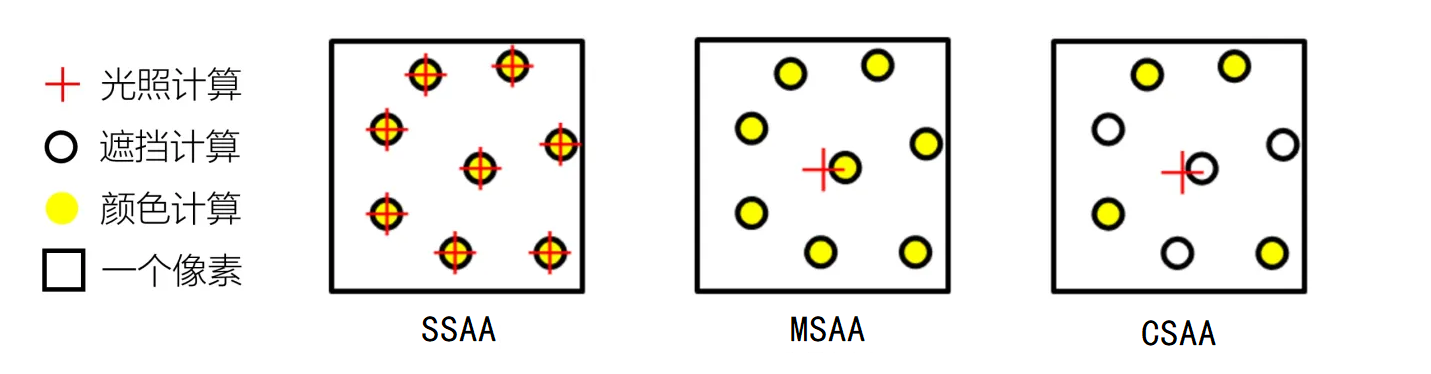
快速近似抗锯齿 FXAA

FXAA（Fast Approximate Anti-Aliasing 快速近似抗锯齿）是一种图像后处理技术。它先直接采样得到目标图像，然后通过像素颜色检测边缘。这种方法使得颜色变化剧烈的像素会被认为是边缘，精度可能不好，但是处理速度非常快。

它不属于先前的信号反走样思路，而是属于一种让画面看上去更舒服的后处理技巧。后处理技术的抗锯齿方法一般没倍数概念，这是因为图像不存在放大。

帧间抗锯齿 TAA

TAA（Temporal Anti-Aliasing 帧间抗锯齿）是最常用的图像后处理技术。

TAA 的核心思想是将采样点从单帧分布到多个帧上（从时间的维度上去采样），即对上一帧图像对应的位置进行采样，得到的像素以一定比例混入当前帧的图像像素中，这样当连续的多个帧的数据混合起来以后，就相当于对每个像素进行了多次采样。

采样时还需要进行抖动操作（即每帧采样的位置有一定随机偏移），这是避免画面静止时导致重复对相同的位置采样从而导致整个图像相当于采样次数没有增加，造成抗锯齿失效。

其中，TAA 使用了运动矢量（motion vector）来确定前一帧在何处进行采样，然后将与当前帧的像素进行混合。

所谓运动矢量，其实就是一个空间中的物体（更准确说是物体像素点）在上一帧的位置与下一帧的位置之差，这往往要借助G Buffer信息来找到，具体算法稍微复杂。

TAA 的缺点是，由于每一帧图像的像素颜色实际上是根据以前的帧来进行混合的，因此容易产生画面延迟感；而且当物体运动过快时，会出现物体的残影现象。

深度学习超采样 DLSS

DLSS（Deep Learning Super Sampling 深度学习超采样技术）则是 NVIDIA 在 Turing 架构的时候推出的基于深度学习方法的图像后处理技术。利用NVIDIA神经图形框架NGX，在超级计算机中以极低的帧率和每像素64个样本对数万张高分辨率的精美图像进行离线渲染，训练出一个深度神经网络。基于无数个小时的训练所获得的数据，网络就可以将分辨率较低的图像作为输入，输出一个高分辨率的精美图，并在一定程度上避免了出现 TAA 等传统方法的模糊、不清晰和透明问题。

DLSS 也不属于先前介绍的信号反走样思路，而是通过低分辨率画面去 ”猜测“ 出高分辨率画面，这种猜出来的信息已经不算是来源于正确的原始信号了。

物体先后关系判定

解决了走样问题之后，还有一个仍需解决的问题，我们如何判断物体先后关系？更具体的说每个像素点所对应的可能不止一个三角形面上的点，我们该选择哪个三角形面上的点来显示呢？

答案显然易见，离摄像头最近的像素点显示。这里便要利用到我们之前做 model−view−projection 变换之后所得到的深度值 z 了，这里定义 z 越大离摄像机越远！

Painter’s Algorithm 画家算法

Painter’s Algorithm 画家算法的灵感来自于画家的绘画方式，从后往前绘制，在 framebuffer 中覆盖即可:

需要深度排序 (n个三角形的O(n log n))，会不会有无法解决的深度排序呢？有的：

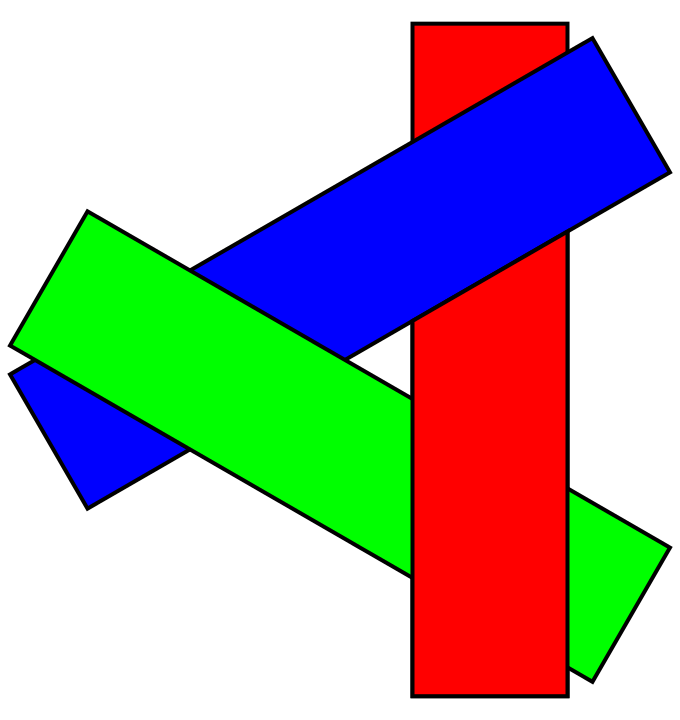
Z-Buffer 深度缓冲

以下我们介绍 Z-Buffer 算法，主要有两步。

1、Z-Buffer 算法需要为每个像素点维持一个深度数组记为zbuffer，其每个位置初始值置为无穷大（即离摄像机无穷远）。

2、然后遍历每个三角形面上的每一个像素点 [x, y]​ ，如果该点的深度值z，小于 zbuffer[x, y] 中的值，则更新 zbuffer[x, y] 值为该点深度值 z，并同时更新该像素点 [x, y] 的颜色为该三角形面上的该点的颜色。

用伪代码表示如下：

1for (each triangle T)
2    for (each sample (x,y,z) in T)
3        if (z < zbuffer[x,y]) // closest sample so far
4            framebuffer[x,y] = rgb; // update color
5            zbuffer[x,y] = z; // update depth
6        else
7        ; // do nothing, this sample is occluded