简单来说光栅化的目的就是将想要展现的物体给真正现实到屏幕上的过程，因为我们的物体其实都是一个个顶点数据来表示的，如何表这些蕴含几何信息的数据转化为屏幕上的像素就是光栅化所考虑的东西。比如说一条直线，究竟该用哪些像素点去逼近它，一个三角形，又用哪些像素集合表示它，这都是光栅化的过程。本节主要讨论介绍两个直线光栅化和一个三角形光栅化算法以及优化。

直线的光栅化

数值微分DDA算法

数值微分DDA全称 Digital Differential Analyzer 算法，DDA是依据直线的斜率对直线进行绘制的算法。在已知直线的方程 $y=kx+b$ 的情况下，若$|k|$小于0，则可以想象直线是偏向 x 轴的，因此 x 轴的变化是要比 y 轴的要快；若 $|k|$ 大于0，则可以想象直线是偏向 y 轴的，因此 y 轴的变化是要比 x 轴的要快，两种情况光栅化效果图如下所示，算法也较为简单。

当 $|k|<1$ 时，从起点开始画起每次 $x = x+1, y = y+k$ , 并将 y 四舍五入，得到新的x，y就是像素点应该画的地方，当 $|k|>1$ 时，从起点开始画起每次 $y = y+1, x = x+1/k$ , 并将 x 四舍五入，得到新的x，y就是像素点应该画的地方。

 1#include <cmath>
 2#include <iostream>
 3
 4using namespace std;
 5bool pic[50][50];
 6
 7void DrawLine(int x0, int y0, int x1, int y1)
 8{
 9	double k = (y1 - y0) * 1.0 / (x1 - x0);
10	double y = y0;
11	for (auto x = x0; x <= x1; ++x) {
12		pic[(int)round(y)][x] = true;
13		y += k;
14	}
15}
16void ShowPic()
17{
18	for (auto i = 49; i >= 0; --i) {
19		for (auto j : pic[i]) {
20			if (j) cout << '*';
21			else cout << '-';
22		}
23		cout << endl;
24	}
25}
26int main()
27{
28	DrawLine(5, 5, 28, 18);
29	DrawLine(5, 5, 18, 28);
30	ShowPic();
31	return 0;
32}

用控制台模拟就是下面的效果：

中点Bresenham算法

Bresenham算法的思想是将像素中心构造成虚拟网格线，按照直线起点到终点的顺序，计算直线与各垂直网格线的交点，然后根据误差项的符号确定该列像素中与此交点最近的像素。

 1#include <cmath>
 2#include <iostream>
 3using namespace std;
 4bool pic[50][50];
 5void DrawLine(int x0,int y0,int x1,int y1)
 6{
 7	double k = (y1-y0)*1.0/(x1-x0);
 8	double y = y0;
 9	for(auto x = x0 ; x <= x1 ; ++ x) {
10		pic[(int)round(y)][x] = true;
11		y += k;
12	}
13}
14void ShowPic()
15{
16	for(auto i = 49 ; i >= 0 ; -- i) {
17		for(auto j:pic[i]) {
18			if(j) cout << 'x';
19			else cout << 'o';
20		}
21		cout << endl;
22	}
23}
24int main()
25{
26	DrawLine(2,2,48,30);
27	ShowPic();
28	return 0;
29}

用控制台模拟就是下面的效果：

三角形的光栅化

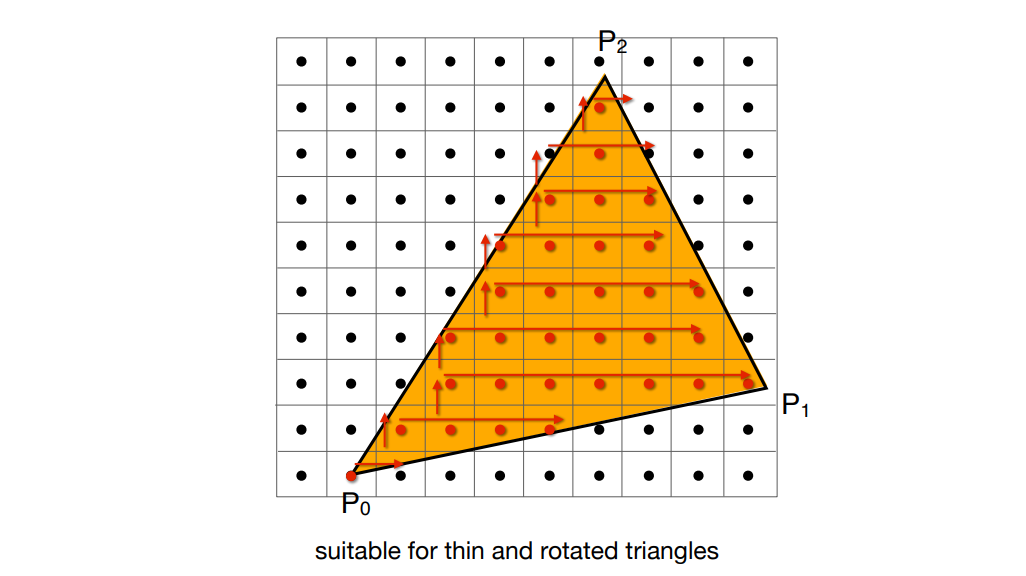
三角形是最基本的多边形，三角形也能保证绝对的平面，对于插值计算来说使用三角形也会方便很多，大部分模型都是使用很多个三角形面表示，因此在做模型的性能考量的时候三角面数是我们经常比较关系的数值。任意的其它多边形其实都可以转化成多个三角形，很多时候我们也把这样的三角形称之为图元，比如下面的小海豚模型：

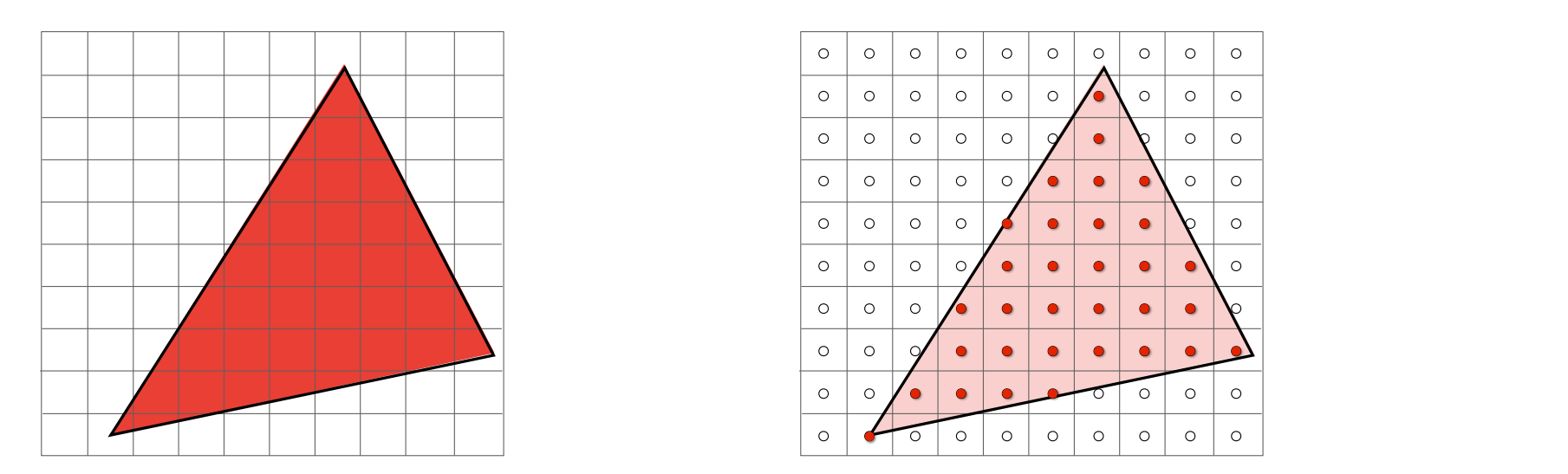
如果对屏幕中的每一个像素进行采样，如果这个像素点在三角形之中那么这个像素点就应该被采用。这里注意需要理解采样的概念，其实采样就是对一个函数做离散，通过一个函数在屏幕的某个点求值，就是采样！比如：判断一个像素点是否在三角形的内部，需要一个函数判断

1for (int x = 0; x < xmax; ++x)
2	output[x] = f(x); 

采样 是图形学的核心思想。同样的我们也可以对时间采样(1D)，面积采样(2D)，方向采样(2D)，体积采样(3D)

接着上面的内容，如何去判断一个点在不在三角形内部呢，那么其中一种办法就是利用叉乘的性质：

我们事先知道想要光栅化的三角形的三个顶点$P_0，P_1，P_2$，以及检测点Q。只要分别计算 $P_0 P_1 \times P_0 Q, P_1 P_2 \times P_1 Q, P_2 P_0 \times P_2 Q$ 如果三者同号则代表点P在三条线段的同一边，那么必然处于三角形内部，如果不同号则代表该点一定在三角形外部，这一点在之前的线性代数基础中也说过。

三角形光栅化优化

通过上面采样的方式，我们得出了每个像素点是否在三角形范围内，但是还有一些对与光栅化过程加速的方法。

AABB 包围盒

包围盒算法是一种求解离散点集最优包围空间的方法。基本思想是用体积稍大且特性简单的几何体（称为包围盒）来近似地代替复杂的几何对象。AABB 包围盒就是采用一个长方体将物体包裹起来，进行两个物体的相交性检测时仅检测物体对应包围盒（包裹物体的长方体）的相交性。AABB 包围盒有一个重要特性，那就是包围盒对应的长方体每一个面都是与某个坐标轴平面平行的，因此，AABB 包围盒又称轴对齐包围盒 。

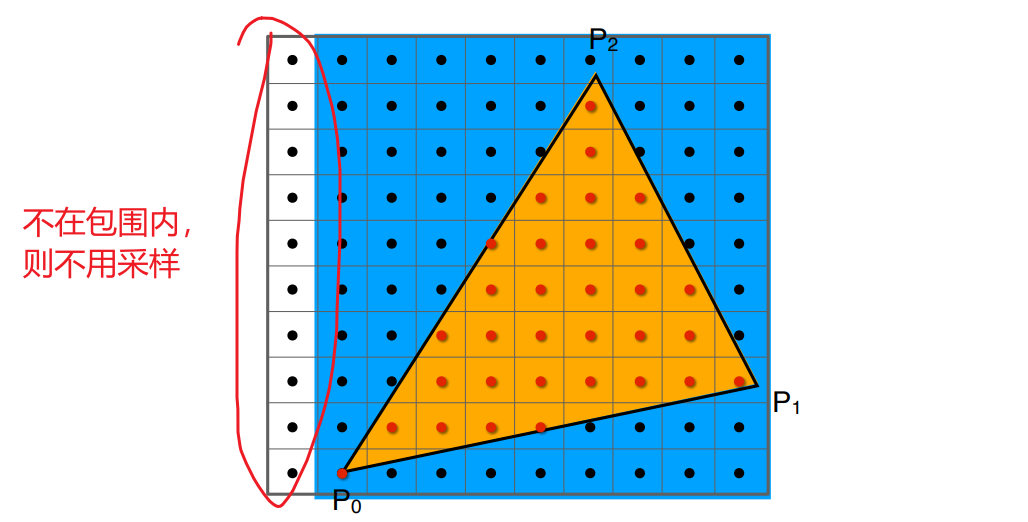
三角形增量遍历