向量与线性代数、变换
最近在 Bilibili 看到了闫令琪大佬讲的图形学教程，直接上链接： https://www.bilibili.com/video/BV1X7411F744 感觉深受启发，作为一门图形学的入门教材，真的讲的通俗易懂，极力推荐感兴趣的同学一起来学习。学习的笔记通过整理以博客的形式展示，今天学习的是图形学中数学（尤其是线性代数相关）的内容 —— 变换矩阵 (Transformation Marices) 在图形学中的重要性不用多说，一切物体的缩放，旋转，位移，都可以通过变换矩阵作用得到。同时在投影变换的时候也有很多应用，本文将会介绍一些简要的变换矩阵以及齐次坐标的由来。
计算机图形学概述
计算机图形学与计算机视觉的区别和联系：
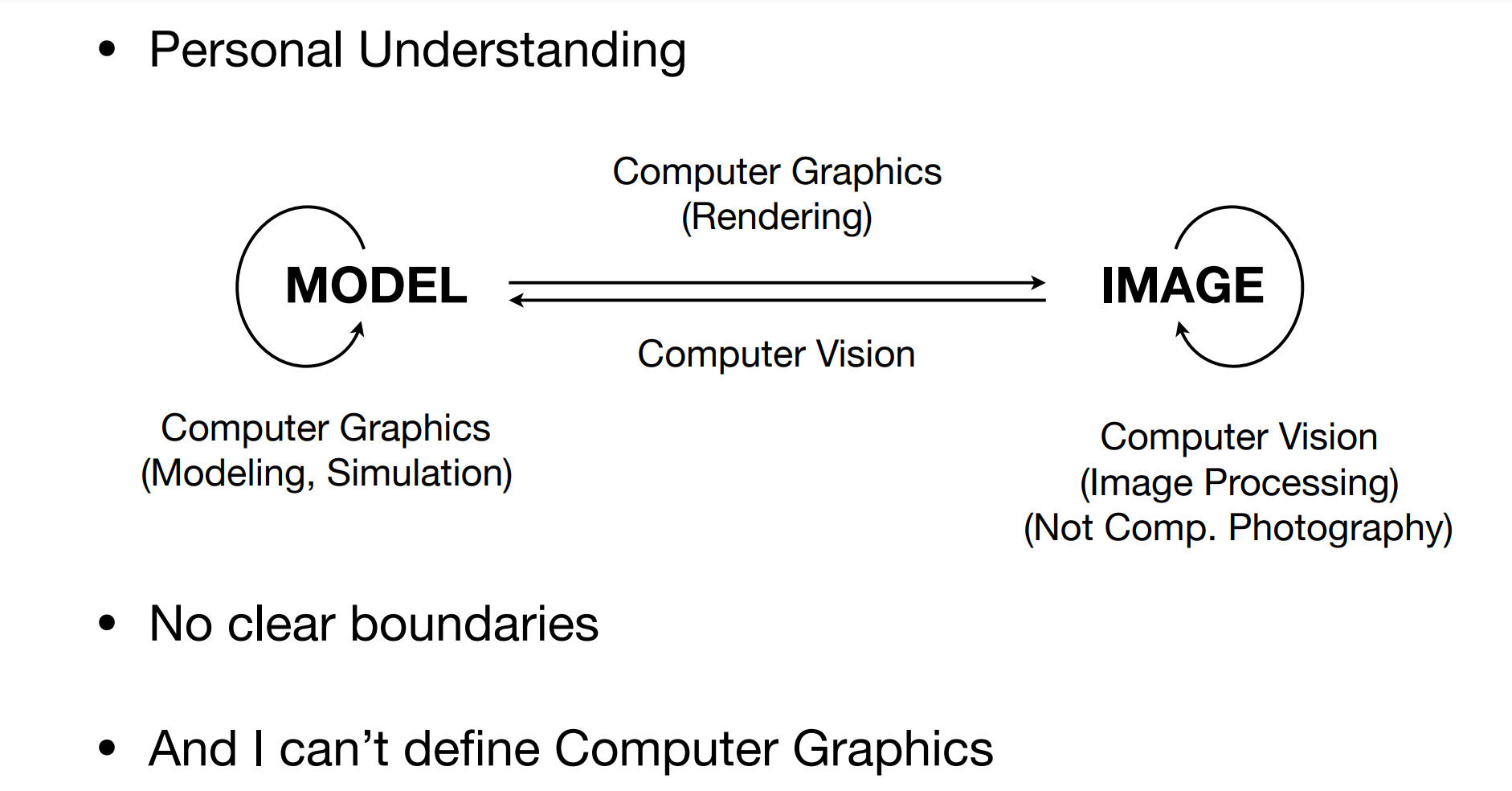
老师挺谦虚的，Like！
向量与线性代数
向量的点积 Dot (scalar) Product
向量点乘的定义：
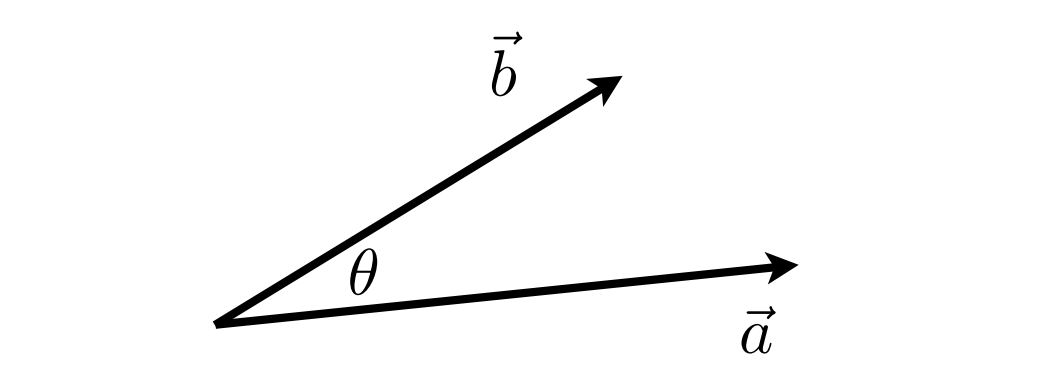$$
\vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}| \cos \theta
$$
则可得出：$\cos \theta=\frac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|}$ ，对于单位向量，向量长度是1，则：$\cos \theta=\hat{a} \cdot \hat{b}$
在2D中： $$ \vec{a} \cdot \vec{b}=\left(\begin{array}{l} x_{a} \ y_{a} \end{array}\right) \cdot\left(\begin{array}{l} x_{b} \ y_{b} \end{array}\right)=x_{a} x_{b}+y_{a} y_{b} $$ 在3D中： $$ \vec{a} \cdot \vec{b}=\left(\begin{array}{c} x_{a} \ y_{a} \ z_{a} \end{array}\right) \cdot\left(\begin{array}{l} x_{b} \ y_{b} \ z_{b} \end{array}\right)=x_{a} x_{b}+y_{a} y_{b}+z_{a} z_{b} $$
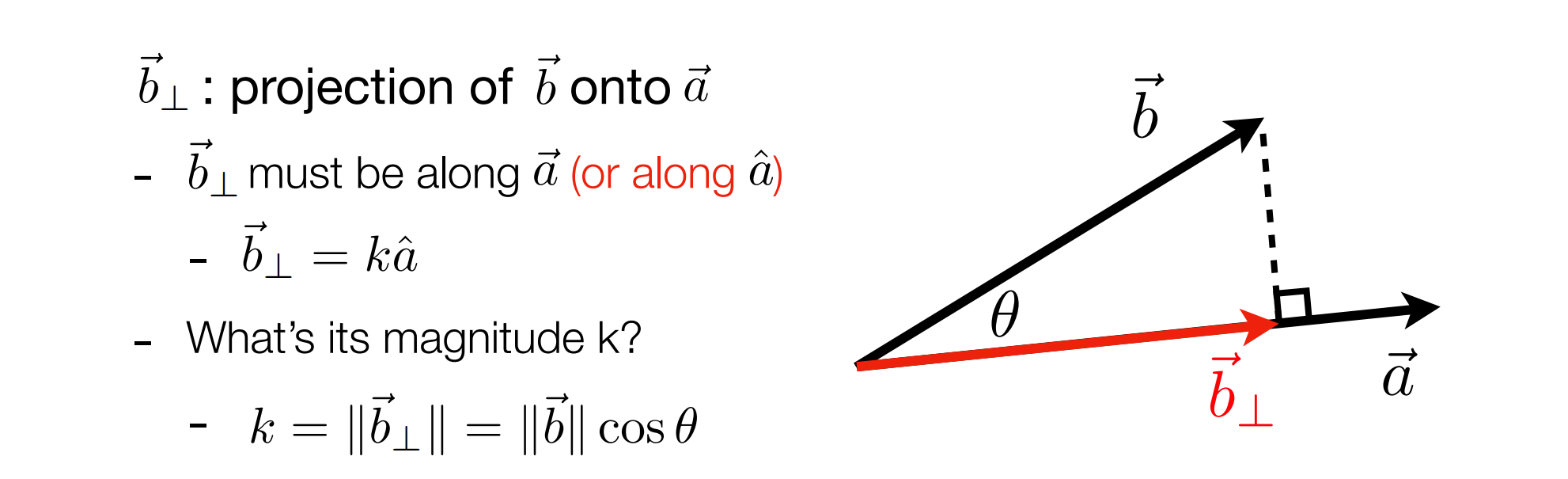
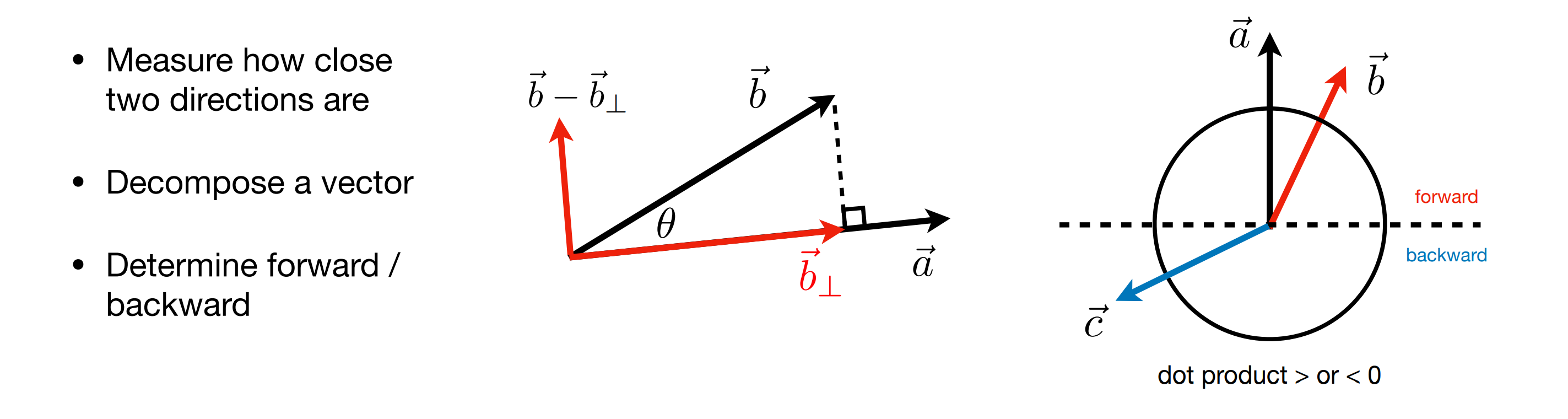
向量点乘在图形学中的应用就是计算投影，并且计算两个向量是 “接近” 还是 “远离”，即两个向量的方向性：
向量的叉积 Cross (vector) Product
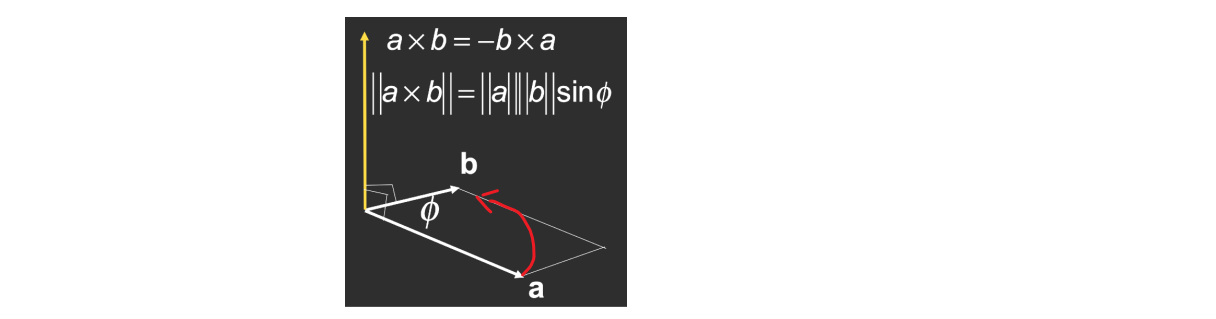
叉积表示与两个初始向量的正交，右手螺旋定则确定叉积的方向，用于构建坐标系（所以右手螺旋定则定义的坐标系又叫右手坐标系）。
$$ \begin{array}{cc} \vec{x} \times \vec{y}=+\vec{z} & \vec{a} \times \vec{b}=-\vec{b} \times \vec{a} \ \vec{y} \times \vec{x}=-\vec{z} & \vec{a} \times \vec{a}=\overrightarrow{0} \ \vec{y} \times \vec{z}=+\vec{x} & \vec{a} \times(\vec{b}+\vec{c})=\vec{a} \times \vec{b}+\vec{a} \times \vec{c} \ \vec{z} \times \vec{y}=-\vec{x} & \vec{a} \times(k \vec{b})=k(\vec{a} \times \vec{b}) \ \vec{z} \times \vec{x}=+\vec{y} & \ \vec{x} \times \vec{z}=-\vec{y} & \end{array} $$
一个向量与自己叉乘得到的是零向量。
叉积的作用：一、确定 “左” 还是 “右”。二、确定 “内” 还是 ”外“。
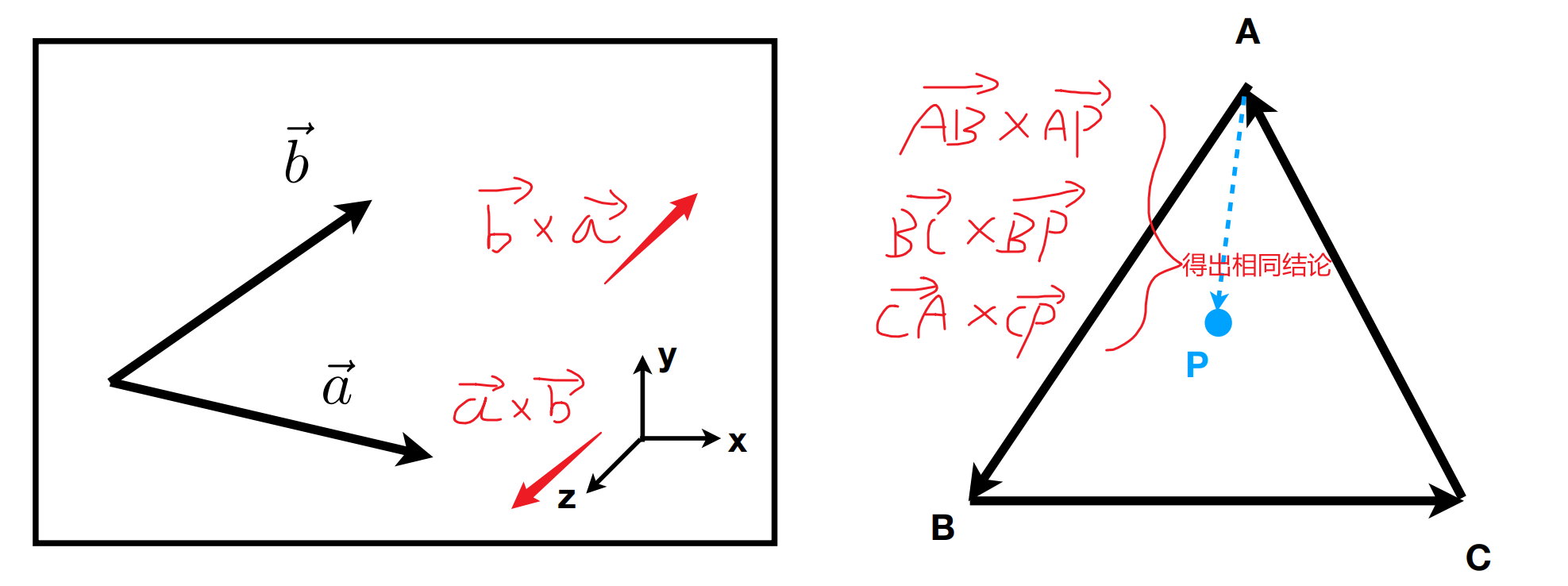
正交坐标系定义： $$ \begin{array}{l} |\vec{u}|=|\vec{v}|=|\vec{w}|=1 \ \vec{u} \cdot \vec{v}=\vec{v} \cdot \vec{w}=\vec{u} \cdot \vec{w}=0 \ \vec{w}=\vec{u} \times \vec{v} \quad \end{array} $$ 所以一个任意一个三维向量均可使用如下方式表示： $$ \vec{p}=(\vec{p} \cdot \vec{u}) \vec{u}+(\vec{p} \cdot \vec{v}) \vec{v}+(\vec{p} \cdot \vec{w}) \vec{w} $$
向量的乘积写成矩阵形式：
点积 Dot (scalar) Product ： $$ \begin{aligned} \vec{a} \cdot \vec{b}=\vec{a}^{T} \vec{b} =&\left(\begin{array}{lll} x_{a} & y_{a} & z_{a} \end{array}\right)\left(\begin{array}{c} x_{b} y_{b} z_{b} \end{array}\right)=\left(x_{a} x_{b}+y_{a} y_{b}+z_{a} z_{b}\right) \end{aligned} $$ 叉积 Cross (vector) Product： $$ \vec{a} \times \vec{b}=A^{*} b=\left(\begin{array}{ccc} 0 & -z_{a} & y_{a} \ z_{a} & 0 & -x_{a} \ -y_{a} & x_{a} & 0 \end{array}\right)\left(\begin{array}{l} x_{b} \ y_{b} \ z_{b} \end{array}\right) $$ 相机在转换不同角度，又在前后移动；那么这些针对相机的操作，就可以通过根据不同矩阵的乘积来完成。
变换（二维与三维）
变换矩阵 (Transformation Marices) 在图形学中的重要性不用多说，一切物体的缩放，旋转，位移，都可以通过变换矩阵作用得到。同时在投影 (projection) 变换的时候也有很多应用，本文将会介绍一些简要的变换矩阵。
1、缩放矩阵 Scale Matrix
缩放变换是一种沿着坐标轴作用的变换，定义如下:
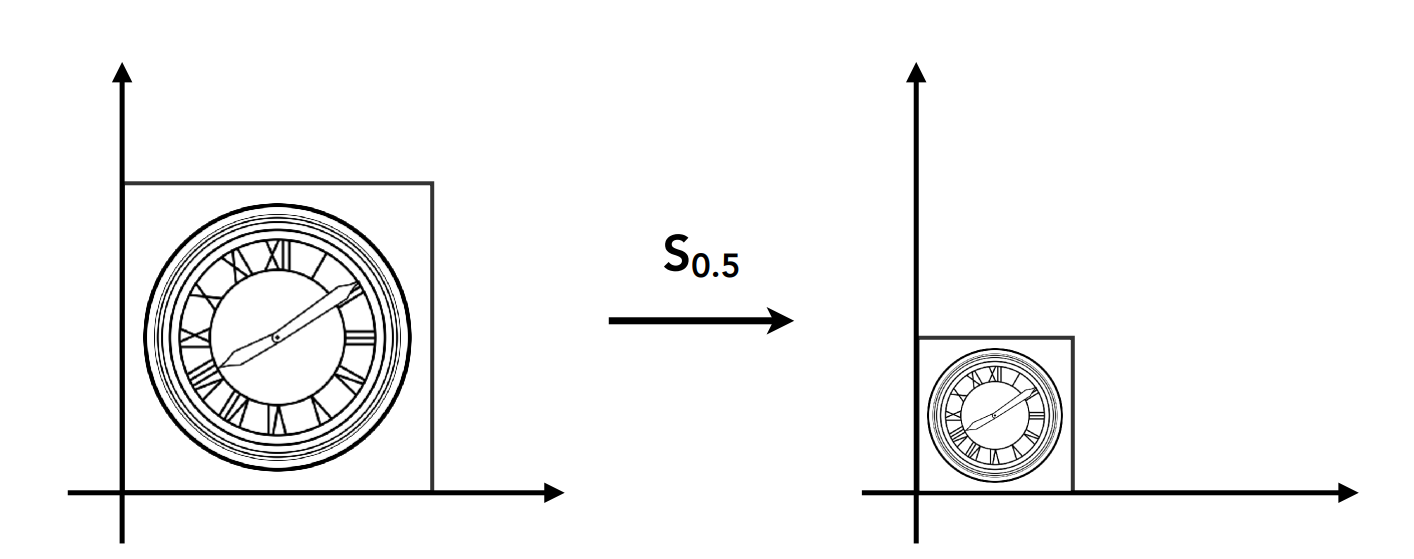$$
\left[\begin{array}{l}
x^{\prime} \
y^{\prime}
\end{array}\right]=\left[\begin{array}{ll}
s & 0 \
0 & s
\end{array}\right]\left[\begin{array}{l}
x \
y
\end{array}\right]
$$
2、缩放矩阵（不均匀缩放） Scale (Non-Uniform)
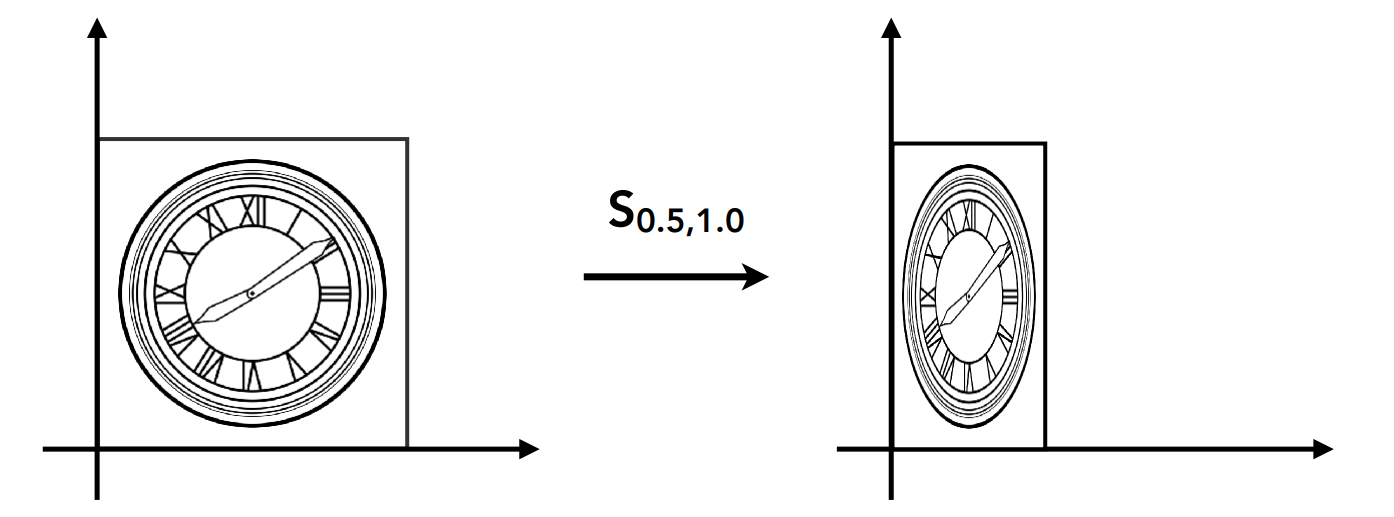$$
\left[\begin{array}{l}
x^{\prime} \
y^{\prime}
\end{array}\right]=\left[\begin{array}{cc}
s_{x} & 0 \
0 & s_{y}
\end{array}\right]\left[\begin{array}{l}
x \
y
\end{array}\right]
$$
3、反射矩阵 Reflection Matrix
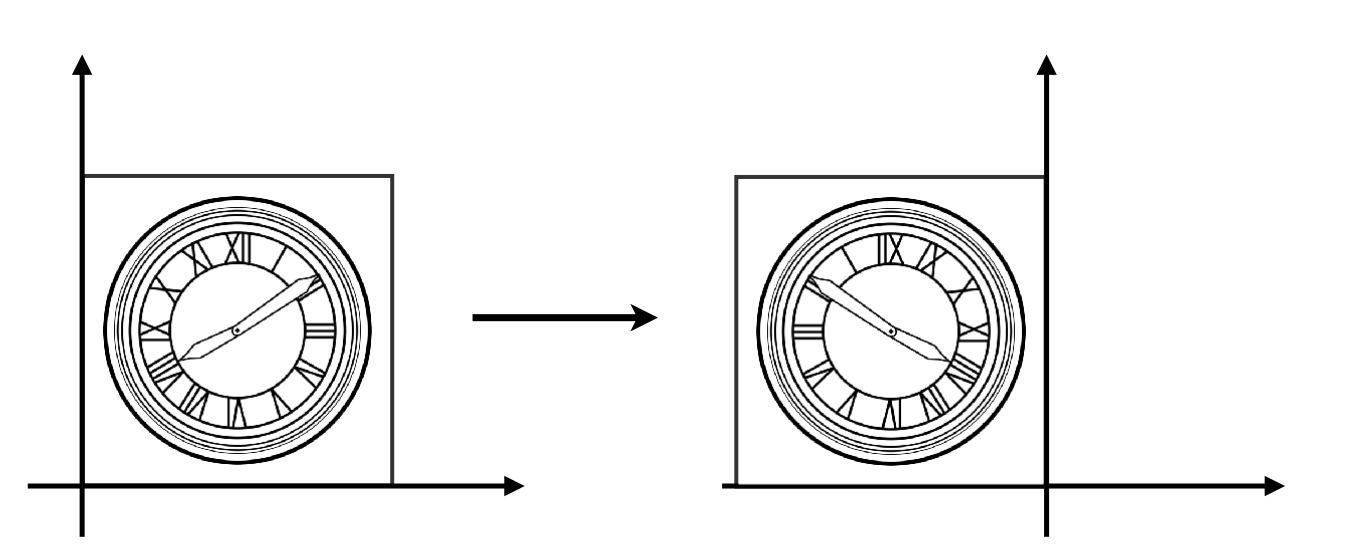$$
\begin{array}{l}
x^{\prime}=-x \
y^{\prime}=y
\end{array} \quad\left[\begin{array}{l}
x^{\prime} \
y^{\prime}
\end{array}\right]=\left[\begin{array}{cc}
-1 & 0 \
0 & 1
\end{array}\right]\left[\begin{array}{l}
x \
y
\end{array}\right]
$$
4、剪切矩阵 Shear Matrix
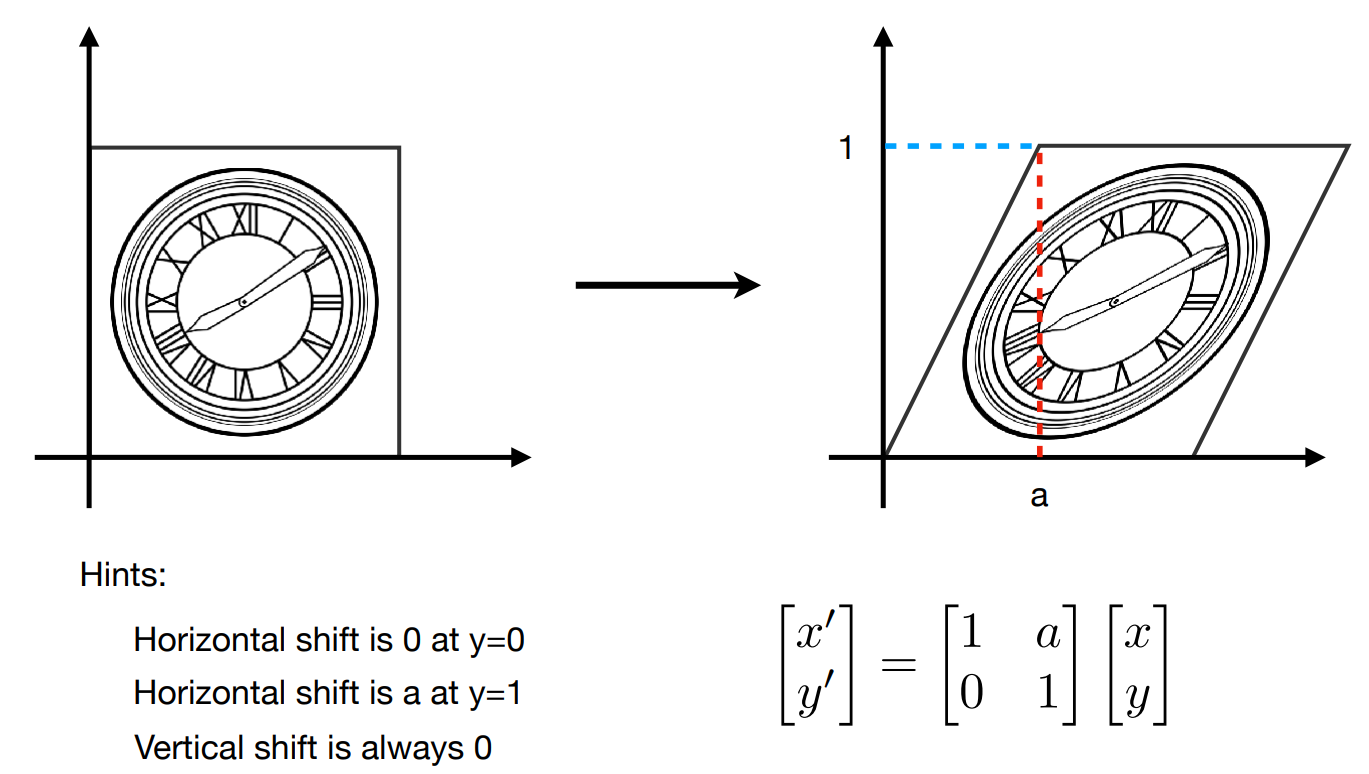
5、旋转矩阵 Rotate Matrix
默认以0, 0点旋转。下面是旋转矩阵的推导：
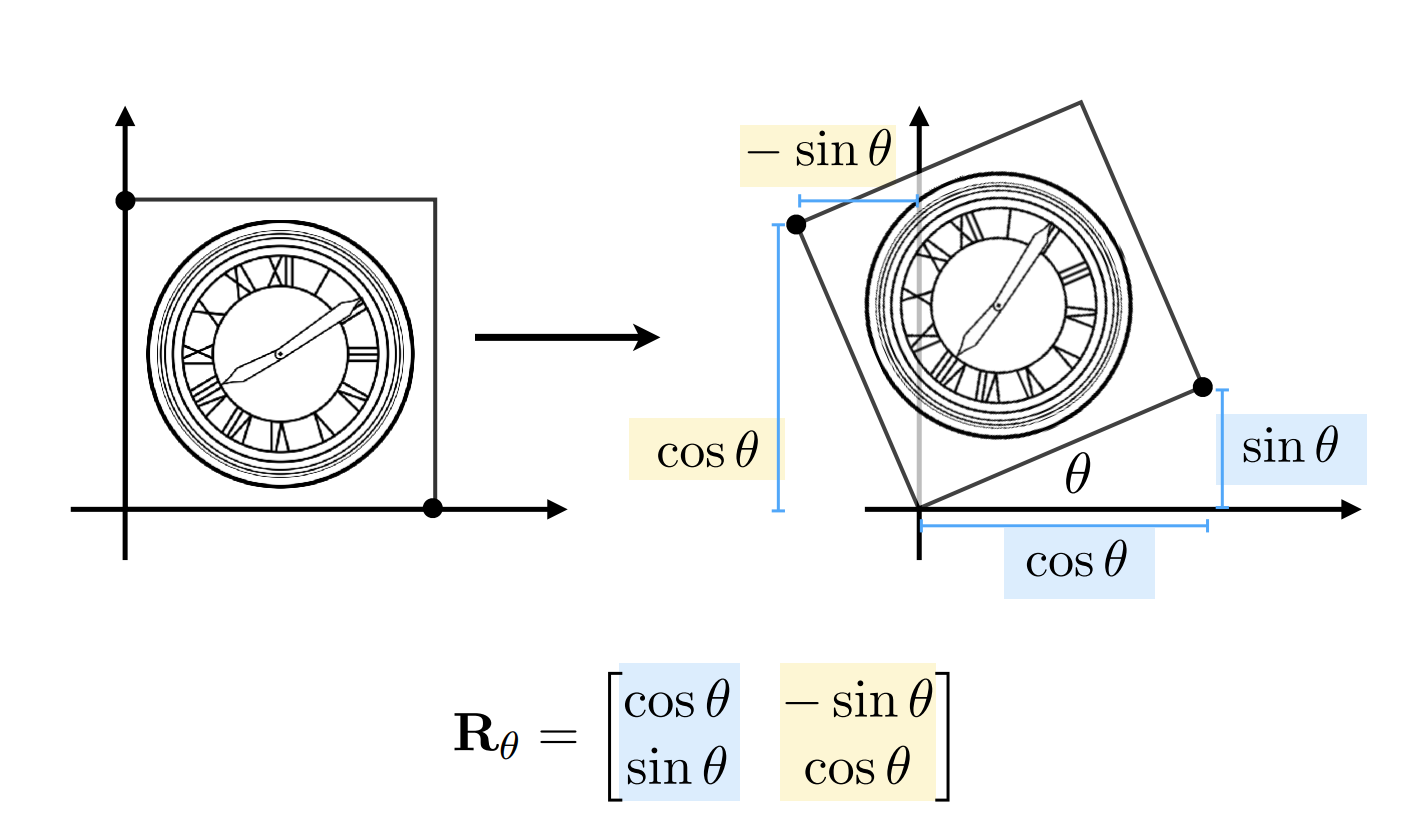
对于旋转矩阵来讲，上面的式子是旋转 θ 角的旋转矩阵，那么如果是旋转 -θ 角呢？ $$ \mathbf{R}_{-\theta}=\left[\begin{array}{cc} \cos \theta & \sin \theta \ -\sin \theta & \cos \theta \end{array}\right] $$ 正好 R(-θ) 是 R(θ) 的转置矩阵，从几何意义来讲， 先变换 θ角度，在变换 -θ 角度，是一个逆操作，所以R(-θ) 是 R(θ) 的逆矩阵。这种互为逆矩阵并且又是转置矩阵的情况，可以称之为正交矩阵。
所以得出结论，所有的旋转矩阵都是正交矩阵。
引入齐次坐标 Homogeneous coordinates
上面的变换都是线性变换，但是有一种特殊的变换不属于线性变换，那就是平移：
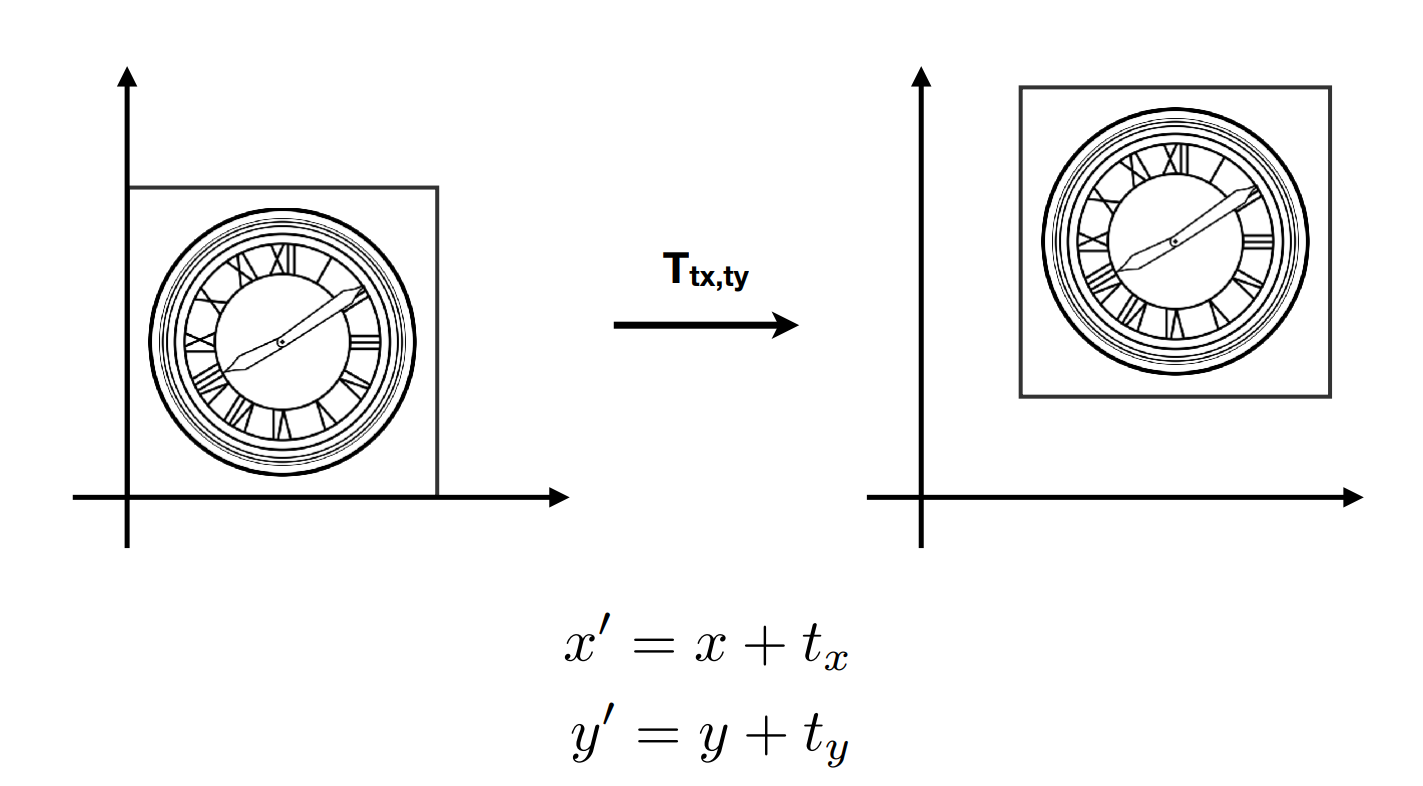
这种变换无法写成矩阵形式，必须通过如下形式才能表示平移操作： $$ \left[\begin{array}{l} x^{\prime} \ y^{\prime} \end{array}\right]=\left[\begin{array}{ll} a & b \ c & d \end{array}\right]\left[\begin{array}{l} x \ y \end{array}\right]+\left[\begin{array}{l} t_{x} \ t_{y} \end{array}\right] $$ 所以平移变换虽然简单，但是不属于线性变换的范畴，但我们不希望平移是一个特例，是否有一种统一的方法来表示所有的转换呢？为了解决这个问题，所以引入了齐次坐标的概念：
更进一步的意义：
点+点即表示两个中点怎么解释呢？其实作为点的话w应该是1，两个点相加w变成了2，怎么变回1呢？直接给w除以2就变回来了，而且此时依旧表示点，通过这个解释来定义两个点的中点。
所以引入齐次坐标实际上是一种归一化的思想，用同一个方式表示了二维空间中的线性变换和具有特殊性的平移变换。在其次坐标系中，为什么0表示方向方向呢？因为的位移没有意义，方向始终不会变！
仿射变换 Affine Transformation
对于任意变换都可写成线性变换+平移的形式，也可以通过齐次坐标写成矩阵的形式， 上面这些保持二维图形的 “平直性” （即变换后直线还是直线不会打弯，圆弧还是圆弧）和 “平行性”（parallelness，其实是指保二维图形间的相对位置关系不变，平行线还是平行线，相交直线的交角不变）的变换就称之为仿射变换
Affine map = linear map + translation： $$ \left(\begin{array}{l} x^{\prime} \ y^{\prime} \end{array}\right)=\left(\begin{array}{ll} a & b \ c & d \end{array}\right) \cdot\left(\begin{array}{l} x \ y \end{array}\right)+\left(\begin{array}{l} t_{x} \ t_{y} \end{array}\right) $$ 使用齐次坐标表示：（下面仅限二维空间的变换情况） $$ \left(\begin{array}{l} x^{\prime} \ y^{\prime} \ 1 \end{array}\right)=\left(\begin{array}{llc} a & b & t_{x} \ c & d & t_{y} \ 0 & 0 & 1 \end{array}\right) \cdot\left(\begin{array}{l} x \ y \ 1 \end{array}\right) $$ 缩放 Scale ： $$ \mathbf{S}\left(s_{x}, s_{y}\right)=\left(\begin{array}{ccc} s_{x} & 0 & 0 \ 0 & s_{y} & 0 \ 0 & 0 & 1 \end{array}\right) $$ 旋转 Rotation ： $$ \mathbf{R}(\alpha)=\left(\begin{array}{ccc} \cos \alpha & -\sin \alpha & 0 \ \sin \alpha & \cos \alpha & 0 \ 0 & 0 & 1 \end{array}\right) $$ 平移 Translation ： $$ \mathbf{T}\left(t_{x}, t_{y}\right)=\left(\begin{array}{ccc} 1 & 0 & t_{x} \ 0 & 1 & t_{y} \ 0 & 0 & 1 \end{array}\right) $$ 思考逆矩阵的意义，一个小例子，想起了之前的看3Blue1Brown的《线性代数的本质》， 其实逆矩阵就是对应着一个变换的逆变换，恢复到原来的样子而已：
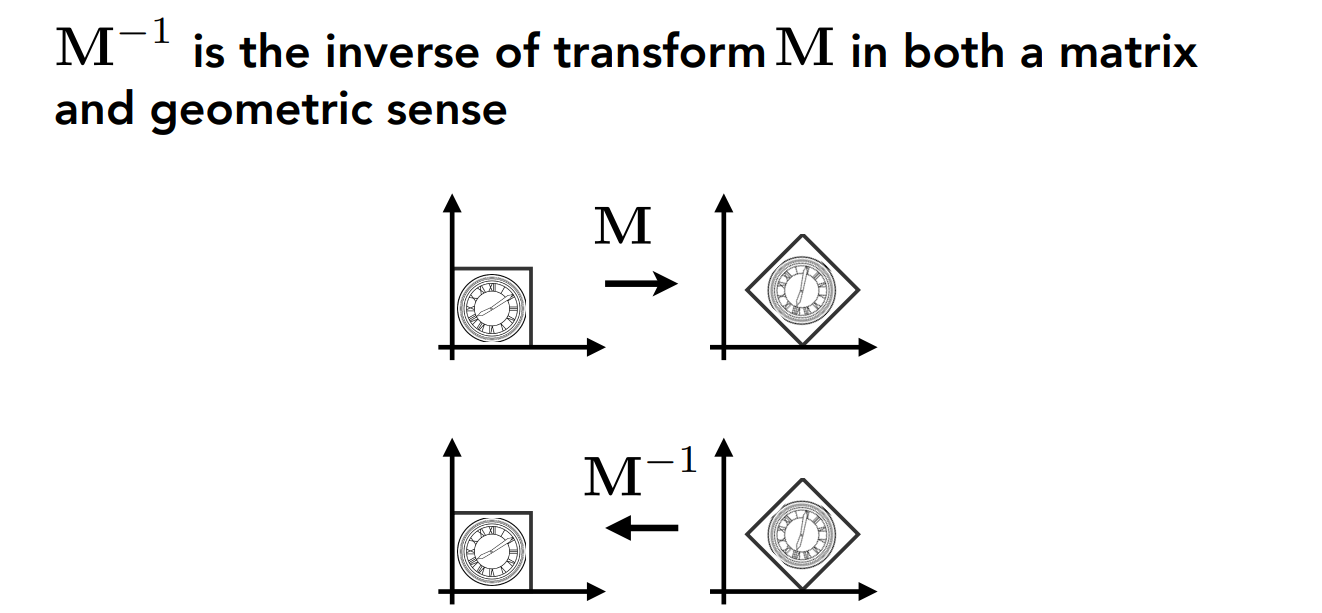
如果矩阵 A 的行列式为 0，与这个方程组相关的变换将空间压缩到更低的维度，此时没有逆变换，正如你不能将一条直线 “解压缩” 成一个平面，至少这不是一个函数能完成的事情。是不是很容易理解？
矩阵乘法顺序几何解释
这也是为什么矩阵乘法不满足交换律的原因，本质就是在逐个应用变换的过程中不能随意更改变换的顺序，否则结果会不一致，从右向左，依次应用对应的变换矩阵。
三维空间中的变换其实也可使用二维的思路，引入另一个变量用于同一三维空间中的仿射变换：
所以我们用 4×4 的矩阵描述 Affine Transformation $$ \left(\begin{array}{l} x^{\prime} \ y^{\prime} \ z^{\prime} \ 1 \end{array}\right)=\left(\begin{array}{lllc} a & b & c & t_{x} \ d & e & f & t_{y} \ g & h & i & t_{z} \ 0 & 0 & 0 & 1 \end{array}\right) \cdot\left(\begin{array}{l} x \ y \ z \ 1 \end{array}\right) $$