哈希切割、Top K问题

问题一：给一个超过100G大小的log file, log中存着IP地址, 设计算法找到出现次数最多的IP地址？ 问题二：与上题目条件相同，如何找出Top K的IP？ 问题三：直接用Linux命令如何实现？

对于问题一：

• 很显然100G的文件直接存入内存中的代价太高了，所以我们需要将文件切分为1000份，逐个加载到内存中
• 将切分后的每个文件中的IP加载到哈希表，由于需要统计次数，所以需要使用哈希表的 Key-Value 模型，使用哈希函数将IP转换为位置int index = IPHash(char* ip)%1000
• 这样的话相同的IP就会映射到相同的位置，执行Value++即可统计次数
• 最后只要一个Key对应着最大的Value即是我们想要的结果

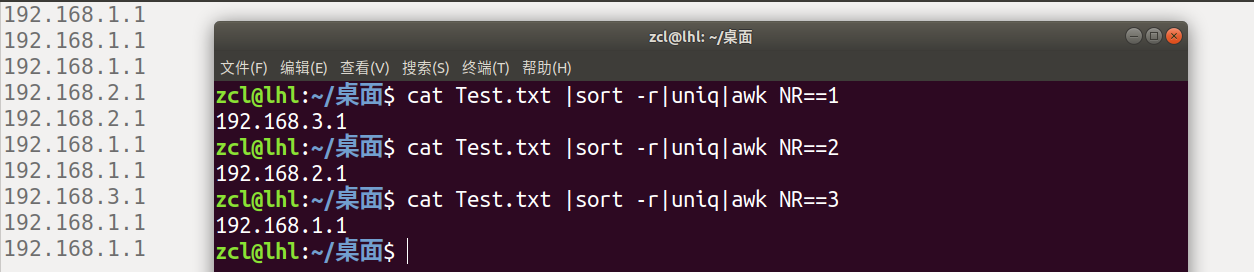
对于问题二： 要想统计次数最多的前K个IP，这里需要建K个元素的小堆，每次选出的IP与堆顶元素比较如果大于堆顶元素就替换掉堆顶元素并且向下调堆，这样到最后堆中的数据就是出现次数最多的前K个IP 对于问题三： cat logfile | sort -r | uniq | awk NR==排行数 先使用sort -r进行次数由多到少的排序，再使用uniq去重，最后使用awk获取结果

位图应用

问题四：给定100亿个整数，设计算法找到只出现一次的整数？ 问题五：给两个文件，分别有100亿个整数，只有1G内存，如何找到两个文件的交集？

对于问题四： 分析一下100亿个数字需要的内存：4×100 ×10^8 / 1024/1024/1024 = 37.252G 很显然与题目一类似，可以将这100亿个数字分100份分别存储在文件中，通过int index = NumHash(int num) %100 哈希切分，在每份文件中找出只出现一次的数字，最后将这100分文件结果归纳在一起即可找出！ 但是可以使用位图来解决这种 存在与否、出现一次 的问题，如果是判断存不存在之类的问题可以使用一个位就可以表示，如：0表示不存在，1表示存在，在本题目中统计只出现一次则需要使用一个位来表示，0表示不存在或者出现多次，1表示只出现一次！

对于问题五： 也是只有1G内存，在这里两个文件则需要使用两个位图，然后根据两个位图的交集，也就是将两个位图&操作来求出两个文件的交集！

位图变形

问题六：1个文件有100亿个int,1G内存,设计算法找到出现次数不超过2次的所有整数

对于问题六： 这个问题实际上是问题四的变形，分析可知不超过两次的情况直接使用两个比特位来完成，00表示0次，01表示一次，10表示两次，11表示超过两次，这样处理问题无论怎么变化都是有效的！

布隆过滤器

问题七：给两个文件,分别有100亿个query(查询),我们只有1G内存,如何找到两个文件交集?分别给出精确算法和近似算法? 问题八：如何扩展BloomFilter使得它支持删除元素的操作？ 问题九：如何扩展BloomFilter使得它支持计数操作？

对于问题七：

• 精确算法 现有100亿条查询，预估每一条大小为20字节，算出大小为96.7G，很显然需要特殊的处理，思想和问题一是一致的，先使用哈希函数做分割，可以把这两个文件分别分割为1000个文件，这样问题就变成了逐个求这1000个文件和另外1000个文件的交集，最后再整合结果即可！
• 近似算法 使用布隆进行过滤，将其中的某一个文件映射到位图当中，取另一文件的内容进行比对，如果不存在，那么就不是交集，如果存在，可视为交集！ 注意：虽然布隆在映射时会映射多个位置，但判断是否在位图中存在时还是可能出现误差，故此方法为近似算法！

对于问题八和问题九： 布隆的删除和计数可归为一类问题，原本布隆是一个元素映射到多个位置上，这个位置上的值是一个Key,现在将其改为数据存在的个数，每当映射到相同的位置，该位置上的数进行加1，最后每个位置上的值表示出现某一元素映射到该位的次数！标准的BloomFilter只支持插入和查找两种操作，如果表达的集合是静态集合的时候，在初始化集合大小，确定hash k的个数，控制错误率的基础上，BloomFilter可以很好的满足需求。但是对于一些动态集合，BloomFilter不满足需求了，其不支持删除操作，现引入Counting BloomFilter，能解决相关问题，具体见：https://blog.csdn.net/fuwei736349065/article/details/75642933

倒排索引

问题十：给上千个文件,每个文件大小为1K—100M。给n个词,设计算法对每个词找到所有包含它的文件,你只有100K内存

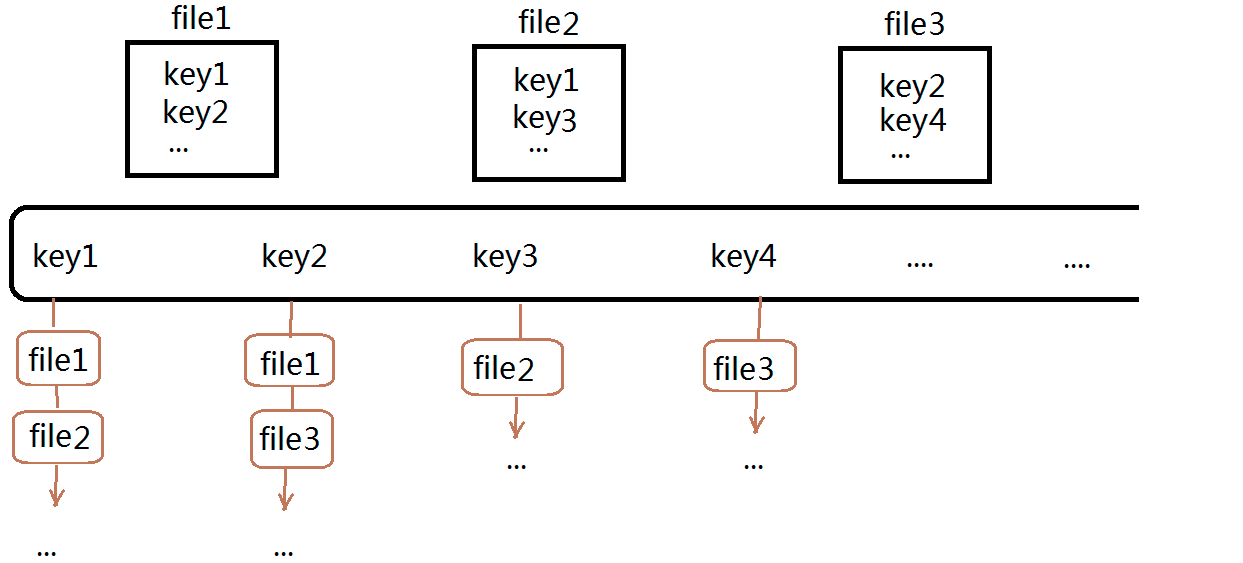
这种做法就是根据文件中的Key去建立哈希表，采用拉链法，凡是包含key的文件都会被挂载到对应的位置，搜索引擎就是这种做法，很显然那些能被百度排在最前面的位置的网页很可能就是在拉链的前几个位置，所以会呈现在前面！