在深度学习的探索旅程中，我们从模拟人类神经网络结构的多层感知器（MLP）开始，逐步探索了非线性预测的实现。通过逻辑回归模型的组合，构建了能够处理复杂预测任务的庞大网络。通过实践我们了解了MLP在图像识别任务中的应用，特别是在处理MNIST数据集时的有效性。但是，面对更高分辨率的图像，MLP模型的局限性就显现出来，因为所需的参数数量巨大，导致计算量大增。为解决这一问题，引入了卷积神经网络（CNN）。

卷积操作 (convolution)

CNN的核心在于卷积操作，它通过滤波器矩阵和图像数据矩阵的相乘和求和来提取图像特征，从而生成新的特征矩阵。卷积操作的目的是快速定位图像中的边缘特征，比如轮廓检测。

这里解释下卷积运算的概念：

$$ A=\begin{bmatrix}X_{11}&X_{12}&X_{13}\X_{21}&X_{22}&X_{23}\X_{31}&X_{32}&X_{33}\end{bmatrix} $$

$$ F=\begin{bmatrix}w_{11}&w_{12}\w_{21}&w_{22}\end{bmatrix} $$

$$ \begin{gathered}A *F=\begin{bmatrix}O_{11}&O_{12}\\O_{21}&O_{22}\end{bmatrix}=\begin{bmatrix}X_{11}w_{11}+X_{12}w_{12}&X_{12}w_{11}+X_{13}w_{12}\+X_{21}w_{21}+X_{22}w_{22}&+X_{22}w_{21}+X_{23}w_{22}\\X_{21}w_{11}+X_{22}w_{12}&X_{22}w_{11}+X_{23}w_{12}\+X_{31}w_{21}+X_{32}w_{22}&+X_{32}w_{21}+X_{33}w_{22}\end{bmatrix}\end{gathered} $$

下面是图像卷积操作的例子（这里不再过多解释，之前使用OpenCV做图像处理的时候，使用到了各种卷积核，本质也就是这里描述的各种过滤器）：

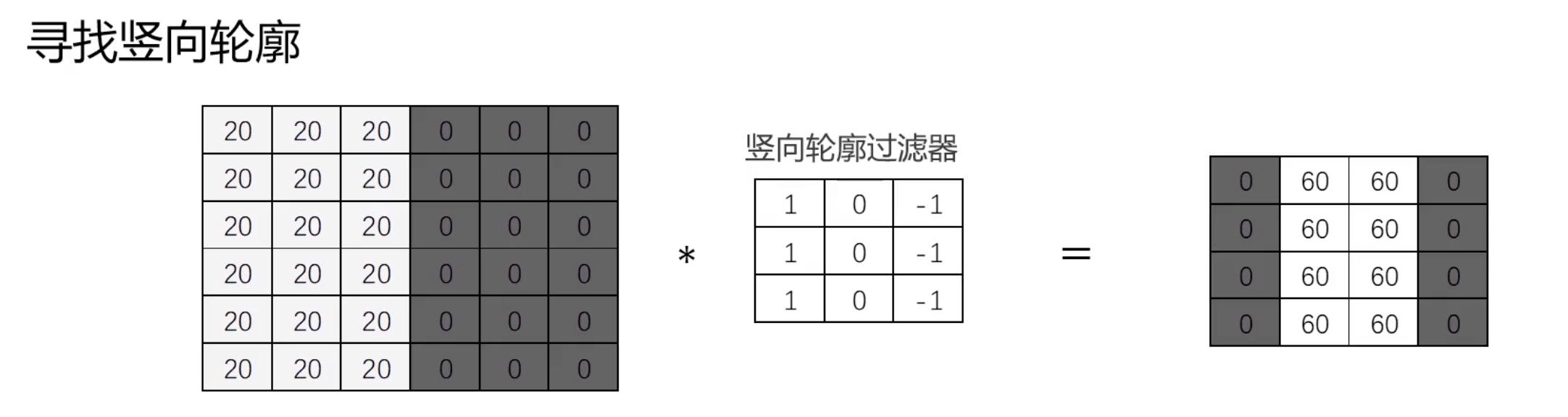
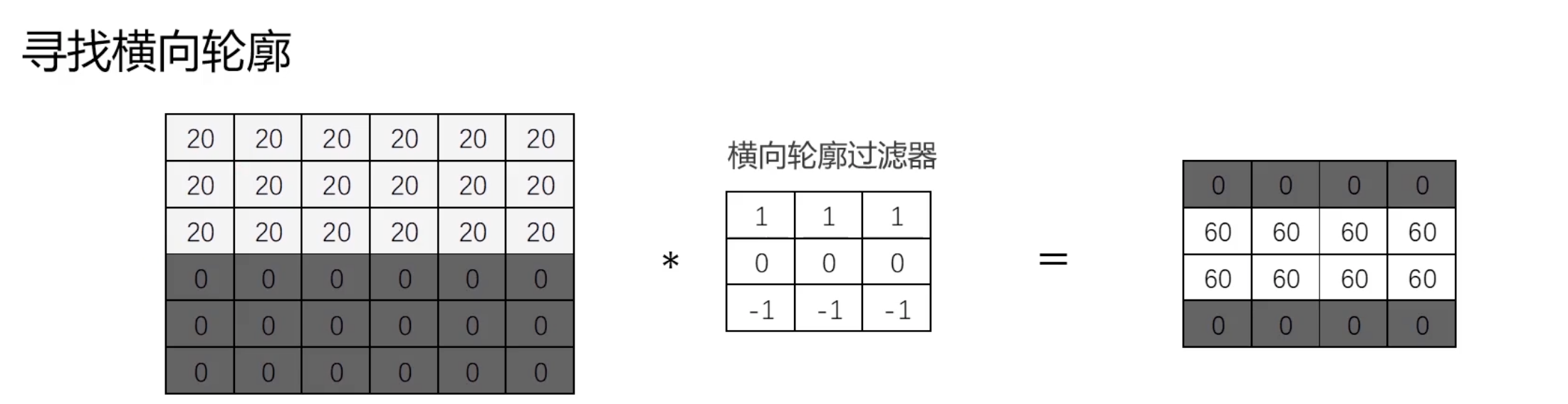
卷积运算通过滑动窗口将滤波器应用于图像的不同部分，每一次操作提取出局部特征，并最终生成一个新的特征矩阵。这个过程大大减少了需要训练的参数数量。所以训练卷积神经网络（CNN）的过程本质上就是学习多个过滤器（或称为卷积核）的参数。这些过滤器在输入数据上滑动，通过卷积操作提取特征。具体来说，训练的目标是通过调整这些过滤器的权重，使得网络能够在给定任务上（如图像分类、目标检测等）表现得更好。

池化操作 (Pooling)

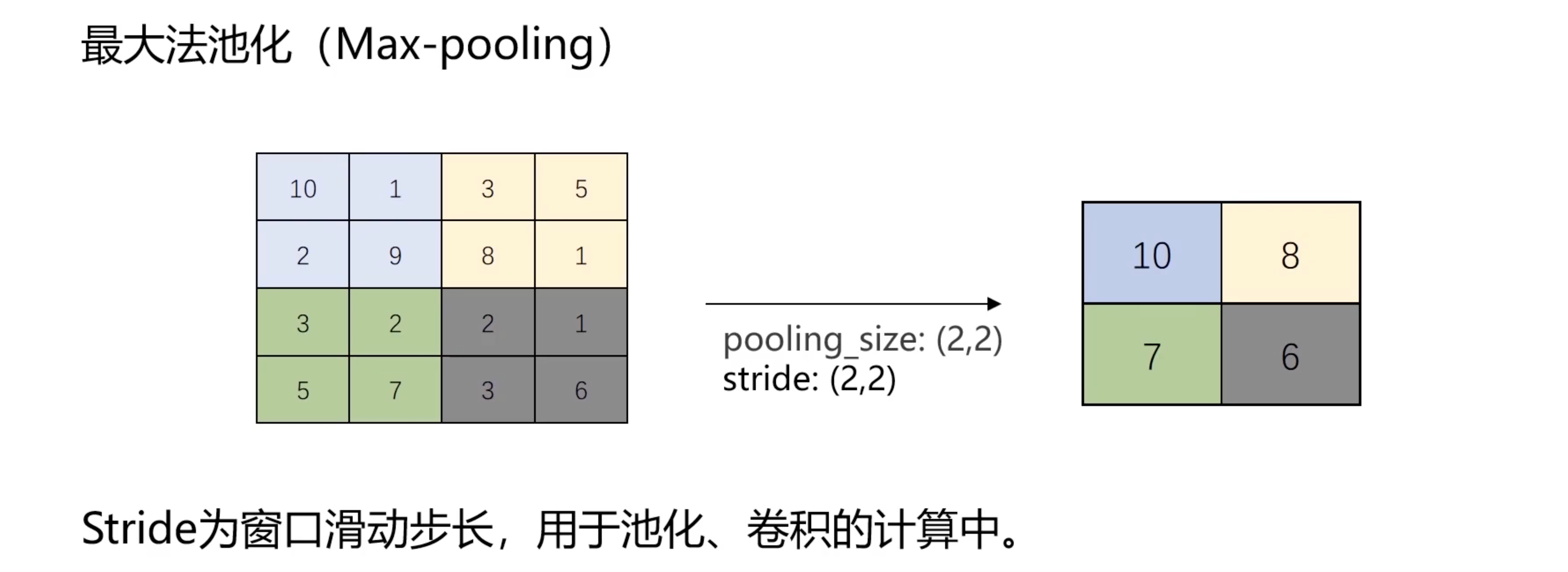
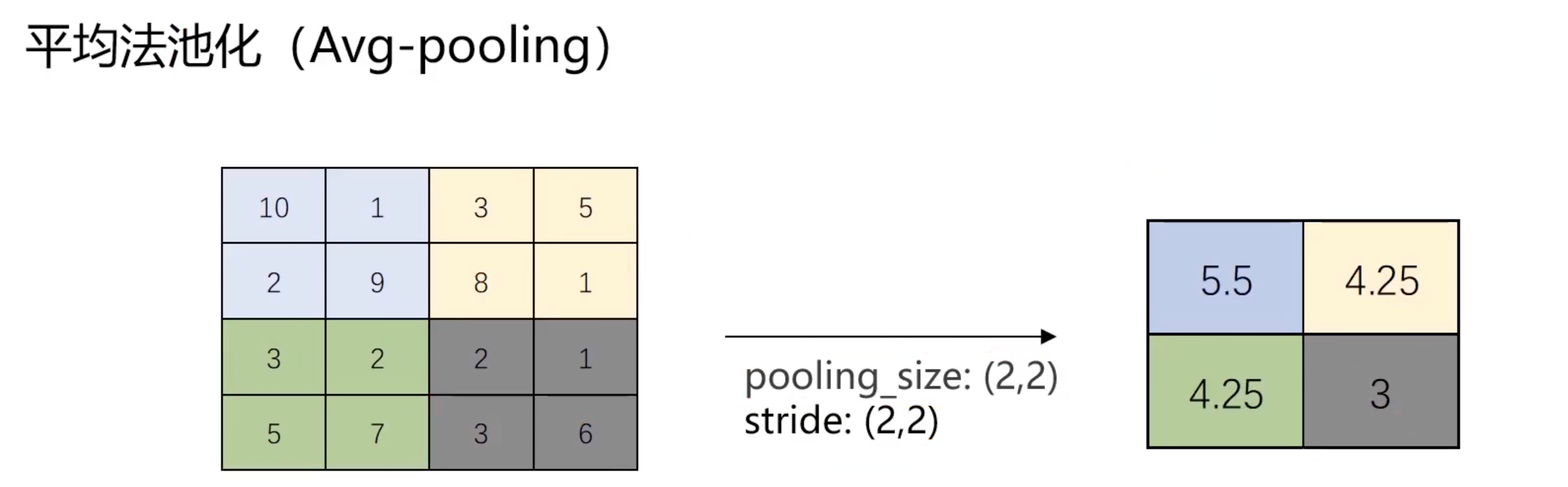
池化操作进一步降低数据的维度，同时保留重要特征。最常见的池化操作是最大池化和平均池化。最大池化提取最显著的特征，而平均池化则提供了特征的平均视图。总结下就是：

• 降维：通过减少特征图的尺寸，降低计算复杂度。
• 特征提取：保留最重要的特征，减少噪声和不必要的细节。
• 增强鲁棒性：对小的平移、旋转或缩放具有不变性。

CNN卷积神经网络

一个典型的CNN包括卷积层、池化层和全连接层。卷积层和池化层负责特征提取，全连接层则负责最终的分类或回归任务。

在卷积和池化之后，通常会使用激活函数，如ReLU（Rectified Linear Unit），以引入非线性因素，增强网络的表达能力。这里顺便一提Relu激活函数：

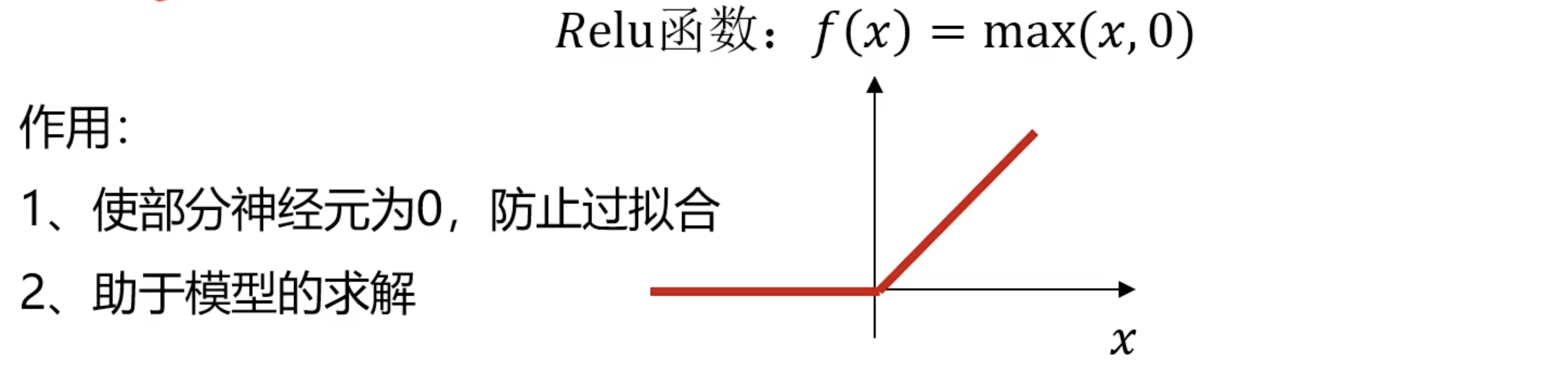
ReLU（Rectified Linear Unit）是深度学习中常用的激活函数，ReLU函数的定义是：

$$ f(x) = max(0, x) $$

ReLU的计算非常简单，当输入为负时，输出为零；当输入为正时，输出等于输入。只需比较输入与零的大小。这使得计算速度快，适合大规模神经网络。ReLU在正区间的梯度为1，有助于缓解梯度消失问题，特别是在深层网络中。另外ReLU会将一些神经元的输出置为零，这导致网络的稀疏性，有助于减少过拟合并提高模型的泛化能力。

CNN两大特点: 参数共享与稀疏连接

CNN之所以优于传统MLP模型，主要归功于以下两点：

1. 参数共享：一个滤波器在整个图像上重复使用，减少了模型参数。与全连接层相比，卷积层的参数数量大幅减少，因为滤波器的参数是共享的。这不仅降低了存储和计算成本，还减少了过拟合的风险。
2. 稀疏连接：每个输出值只与输入中的一小部分相关，减少了计算量。而且有助于提取局部特征，如边缘和角点。这些局部特征可以组合成更复杂的特征，帮助模型更好地理解图像内容。

思考练习题

使用一个4×4×3的滤波器对一个500×400像素的RGB图像进行卷积，卷积默认步长为1，然后应用池化层（pooling_size:(2,2)，strides(2,2)），并计算结果矩阵的维度。

卷积层：给定一个500×400的RGB图像，我们使用一个4×4×3的滤波器进行卷积。因为没有给出步幅和填充，我们假设步幅为1（这是最常见的选择）和填充为0（即，没有填充）。那么卷积层的输出大小可以用以下公式计算： $$ W_{out} = \frac{{W_{in} - F + 2P}}{S} + 1 $$ 其中，$W_{in}$ 是输入宽度，$F$ 是滤波器的大小，$P$ 是填充，$S$ 是步幅。输入宽度和高度是500和400，滤波器的大小是4，填充是0，步幅是1。所以，卷积层的输出大小是：

宽度：$W_{out} = \frac{{500 - 4 + 2*0}}{1} + 1 = 497$

高度：$H_{out} = \frac{{400 - 4 + 2*0}}{1} + 1 = 397$

所以，卷积层的输出是一个497×397的特征映射。

池化层：接下来，我们在卷积层的输出上应用一个2×2的池化操作，步幅为2，填充为2。再次使用上面的公式，我们可以计算出池化层的输出大小：

宽度：$W_{out} = \frac{{497 - 2 + 2*2}}{2} + 1 = 250$

高度：$H_{out} = \frac{{397 - 2 + 2*2}}{2} + 1 = 200$

所以，最终经过池化层后的输出是一个250×200的矩阵。

卷积神经网络总结

卷积神经网络（CNN）是当前图像识别领域的核心技术。通过理解卷积、池化和激活函数的原理，我们可以构建出能够有效处理高分辨率图像的模型，同时大幅减少所需计算资源。通过实践，我们可以更好地掌握CNN在实际应用中的强大能力。