拟合指机器学习模型在训练的过程中，通过更新参数，使得模型不断契合可观测数据（训练集）的过程，但在这个过程中容易出现欠拟合（underfitting）和过拟合（overfitting）的情况：一开始模型往往是欠拟合的，也就是说模型无法得到较低的训练误差，也正是因为如此才有了优化的空间，我们需要不断的调整参数使得模型能够更好的拟合训练集数据，但是优化到了一定程度，模型的训练误差远小于它在测试数据集上的误差，这个时候就需要解决过拟合的问题了。

先看个线性归回的例子：

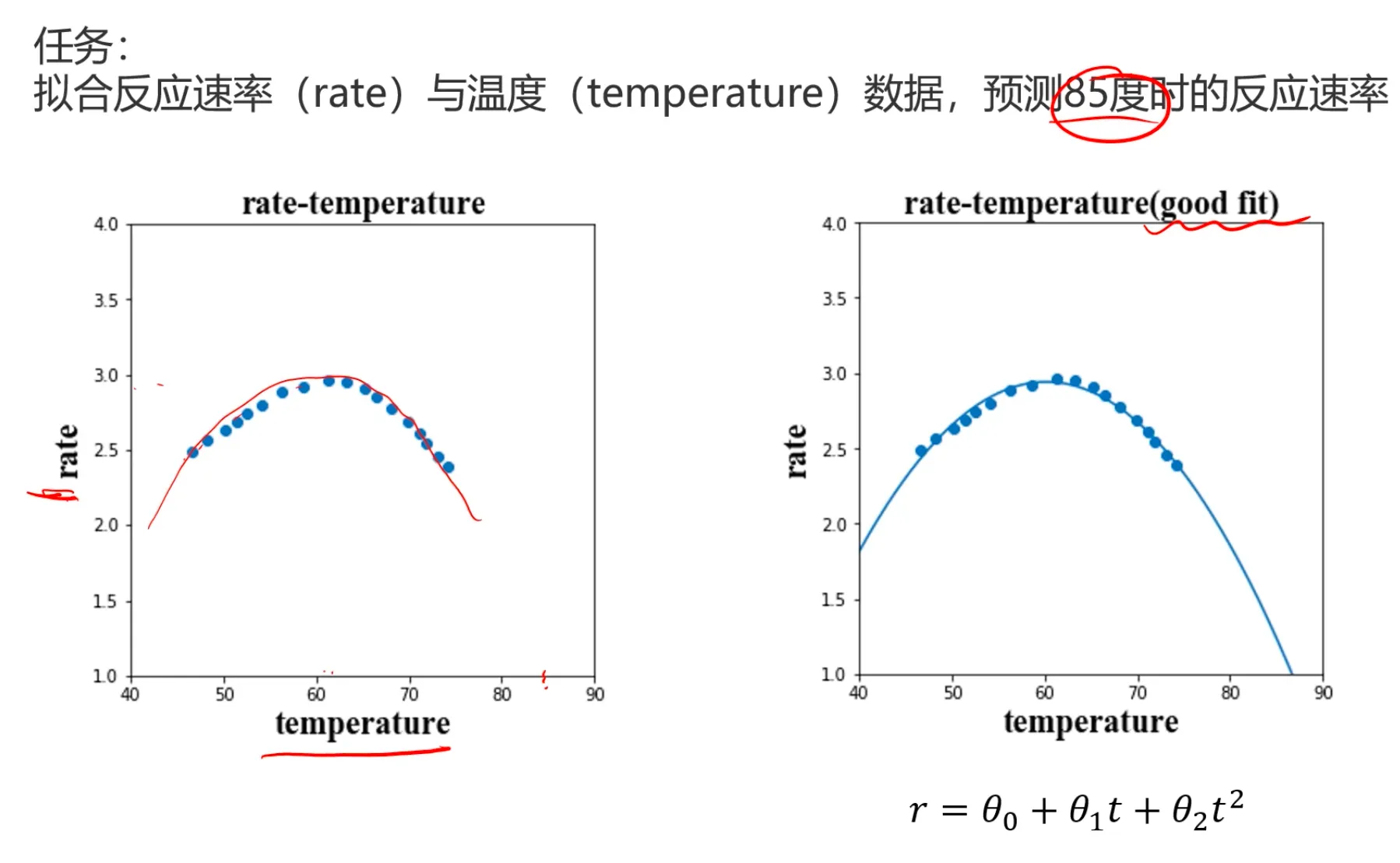
下面是一个酶的活性鱼温度关系的二项式回归模型，可以看到模型非常契合样本数据：

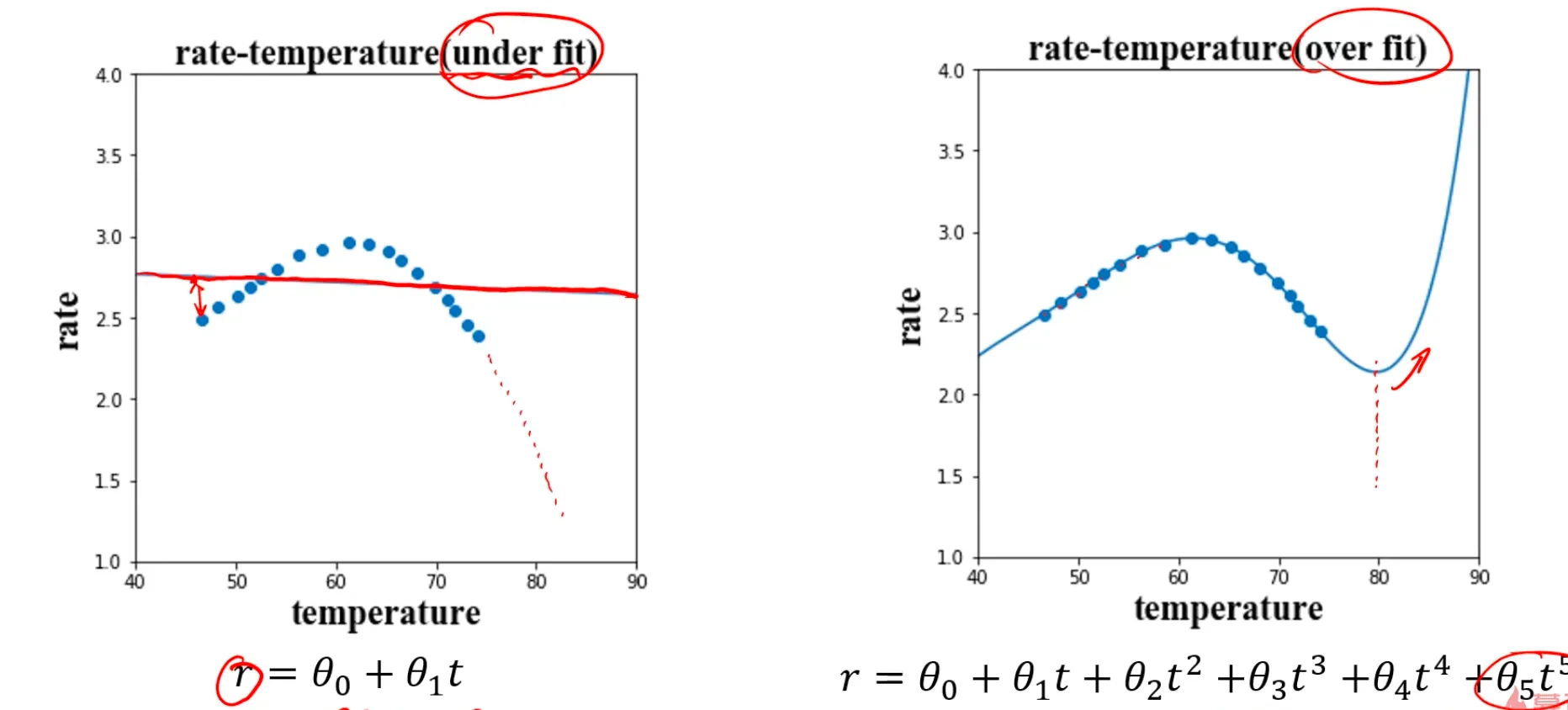
下面则分别是使用单项式回归导致的欠拟合问题，和使用过多附加项的多项式回归导致的过拟合问题：

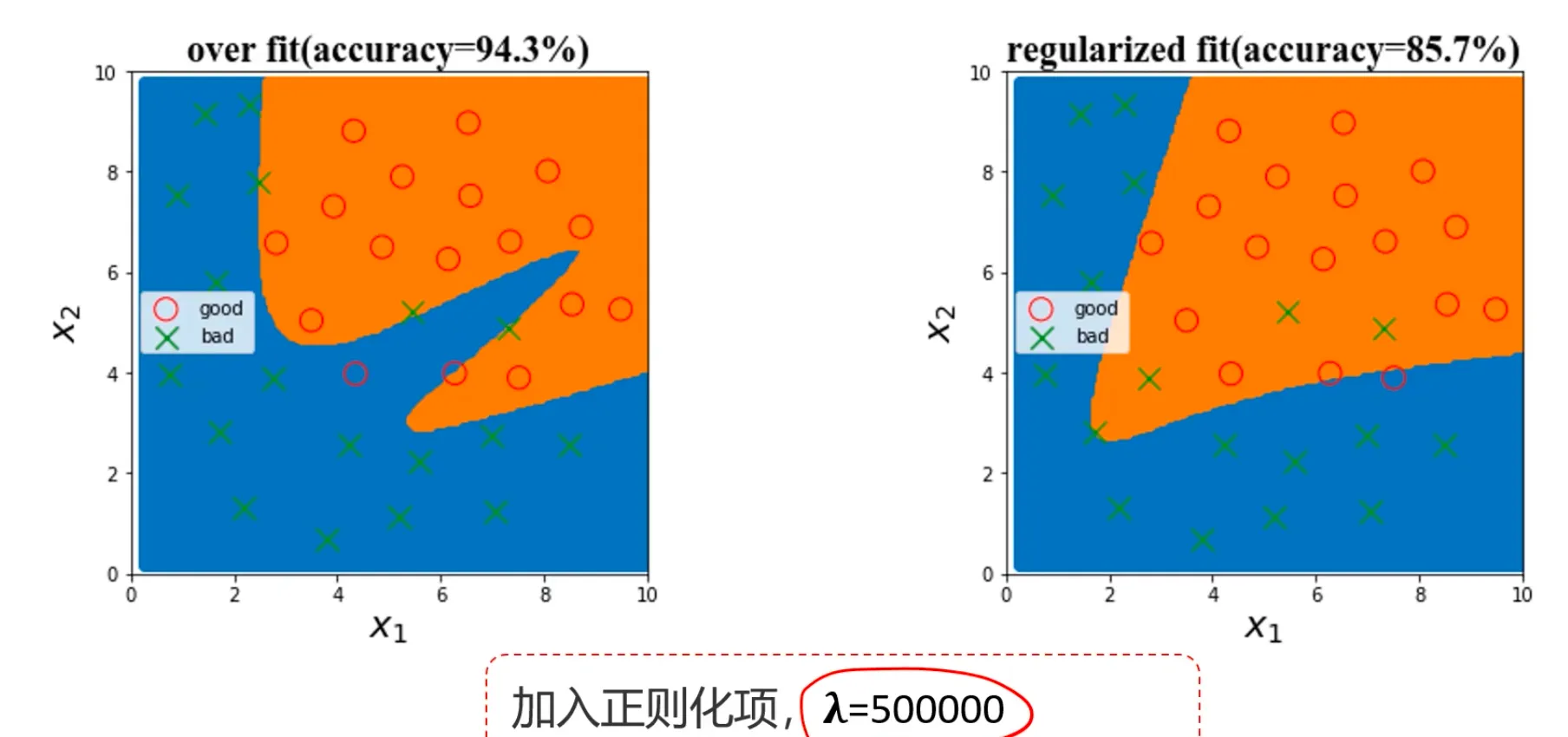
再来看个逻辑回归的例子：

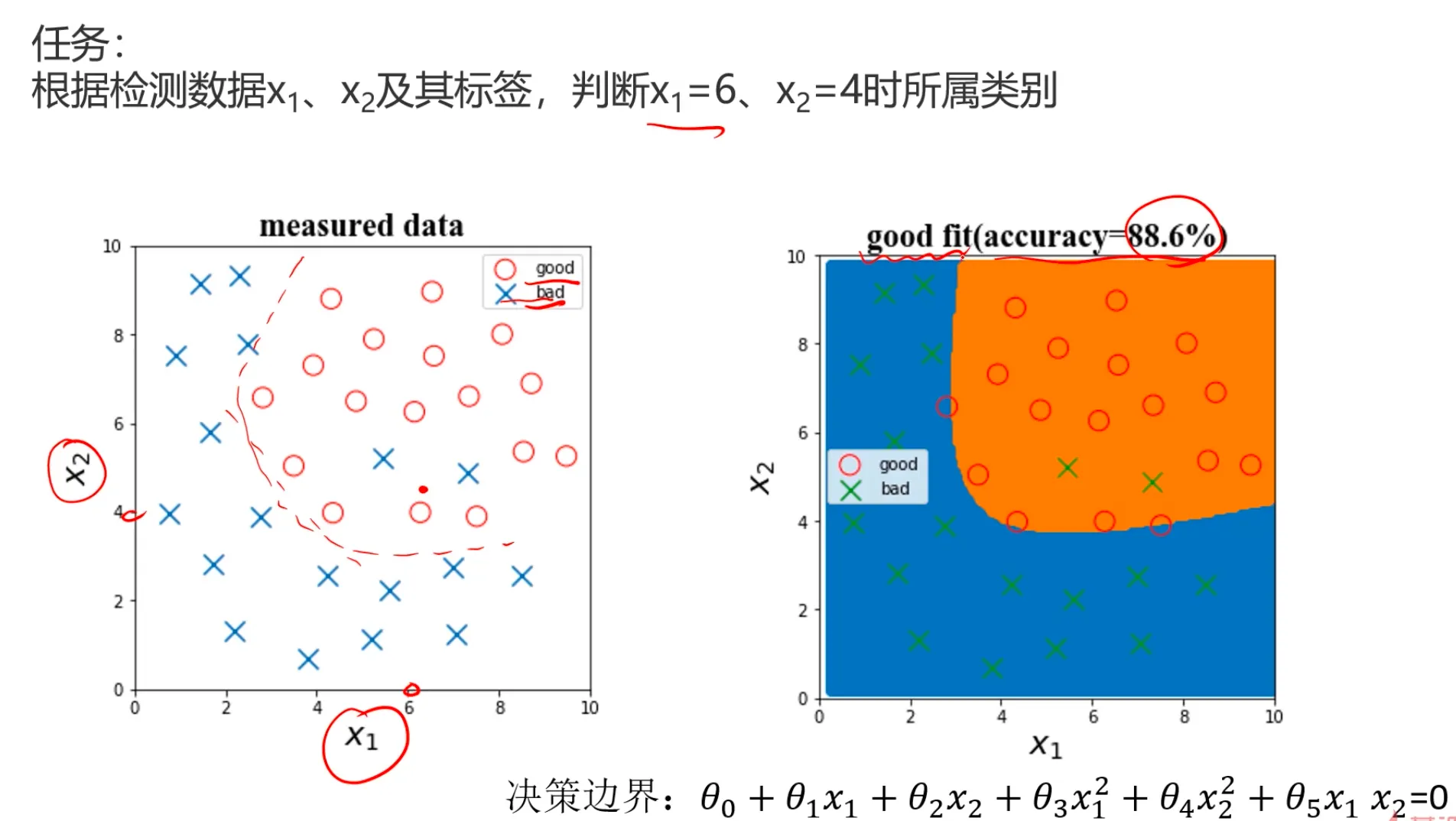
如果是单纯采用一阶边界不管是对于样本数据，还是预测数据都不准确，如果是采用复杂边界曲线，确实能很好的 把样本数据的准确率提的非常高，但是这样的模型一旦用于真实数据时会出现大量的误判，比如图片标注出来的区域，为了能完全拟合样本数据，却错判了实际的真实数据，这就是过拟合的危害。

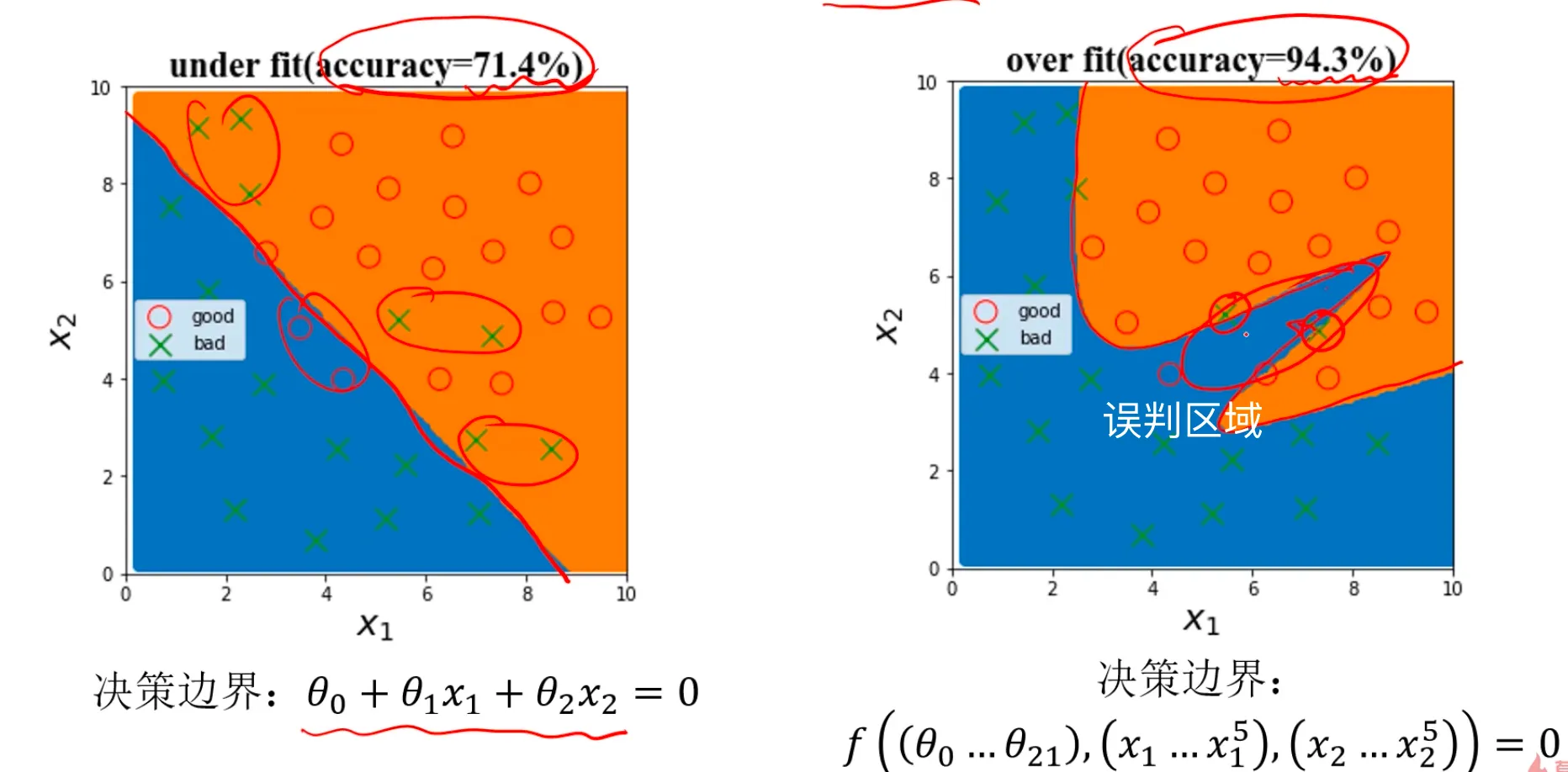
模型不合适的话，会导致无法对数据实现有效预测：

	训练数据	预测数据
欠拟合	不准确	不准确
过拟合	准确	不准确
好模型	准确	准确

欠拟合可以在训练数据的时候就发现问题，因为一对比准确率就知道了，我们可以通过优化模型解决。

:::tip{title=“如何解决过拟合问题”}

导致过拟合问题的原因:

1、模型结构过于复杂维度过高

2、使用了过多属性模型训练时包含了干扰项信息

如何解决过拟合问题？

1、简化模型结构 (使用低阶模型比如线性模型）

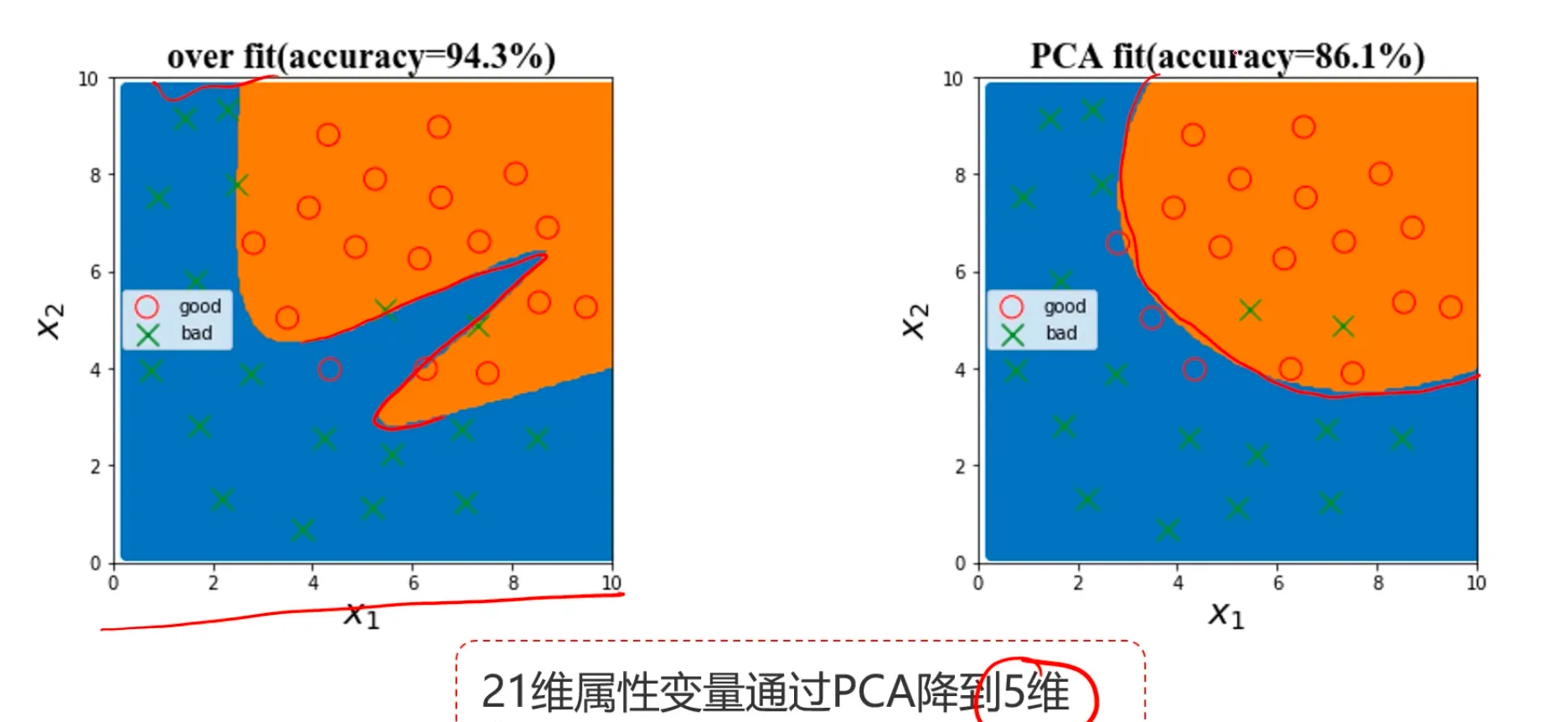
2、数据预处理，保留主成分信息 (数据PCA处理）

3、在模型训练时，增加正则化项 (正则化)

:::

PCA降维：

添加正则项：

拿线性回归来说，添加正则项的主要目的就是限制高次项的影响。

线性回归的损失函数 J ：

$$ J=\frac1{2m}\sum_{i=1}^m(y_i^{\prime}-y_i)^2=\frac1{2m}\sum_{i=1}^m(g(\theta,x_i)-y_i)^2 $$

正则化处理之后的损失函数 J：

$$ J=\frac1{2m}\sum_{i=1}^m(g(\theta,x_i)-y_i)^2+\frac\lambda{2m}\sum_{j=1}^n\theta_j^2 $$

通过引入正则项，在 $\lambda$ 取值比较大的情况下，可以约束 $\theta$ 的值，有效控制各个属性数据的影响。

对于逻辑回归来说： $$ \begin{aligned} &J=\frac{1}{m}\sum_{i=1}^{m}J_{i}=-\frac{1}{m}\biggl[\sum_{i=1}^{m}\bigl(y_{i}\log\bigl(P(x_{i})\bigr)+(1-y_{i})\log\bigl(1-P(x_{i})\bigr)\bigr)\biggr] \ &=-\frac1m\biggl[\sum_{i=1}^m\bigl(y_i\log\bigl(g(\theta,x_i)\bigr)+(1-y_i)\log\bigl(1-g(\theta,x_i)\bigr)\bigr)\biggr] \end{aligned} $$

添加正则项： $$ J=-\frac1m\left[\sum_{i=1}^m(y_i\log(g(\theta,x_i))+(1-y_i)\log(1-g(\theta,x_i)))\right]+\frac\lambda{2m}\sum_{j=1}^n\theta_j^2 $$