神奇的卷积核
关于卷积
卷积是分析数学中一种重要的运算。卷积是一种线性运算,图像处理中常见的mask运算都是卷积，广泛应用于图像滤波。高斯变换就是用高斯函数对图像进行卷积，卷积操作是图像变换的基础。
如果我们称$(f * g)(n)$是f、g的卷积：
连续型卷积的公式 $$ (f * g)(n)=\int_{-\infty}^{\infty} f(\tau) g(n-\tau) d \tau $$
离散型卷积的公式 $$ (f * g)(n)=\int_{\tau=-\infty}^{\infty} f(\tau) g(n-\tau) $$
从中我们可以得出： $$ n=\tau+(n-\tau) $$
假设现有两个骰子，随机掷骰子点数和为4
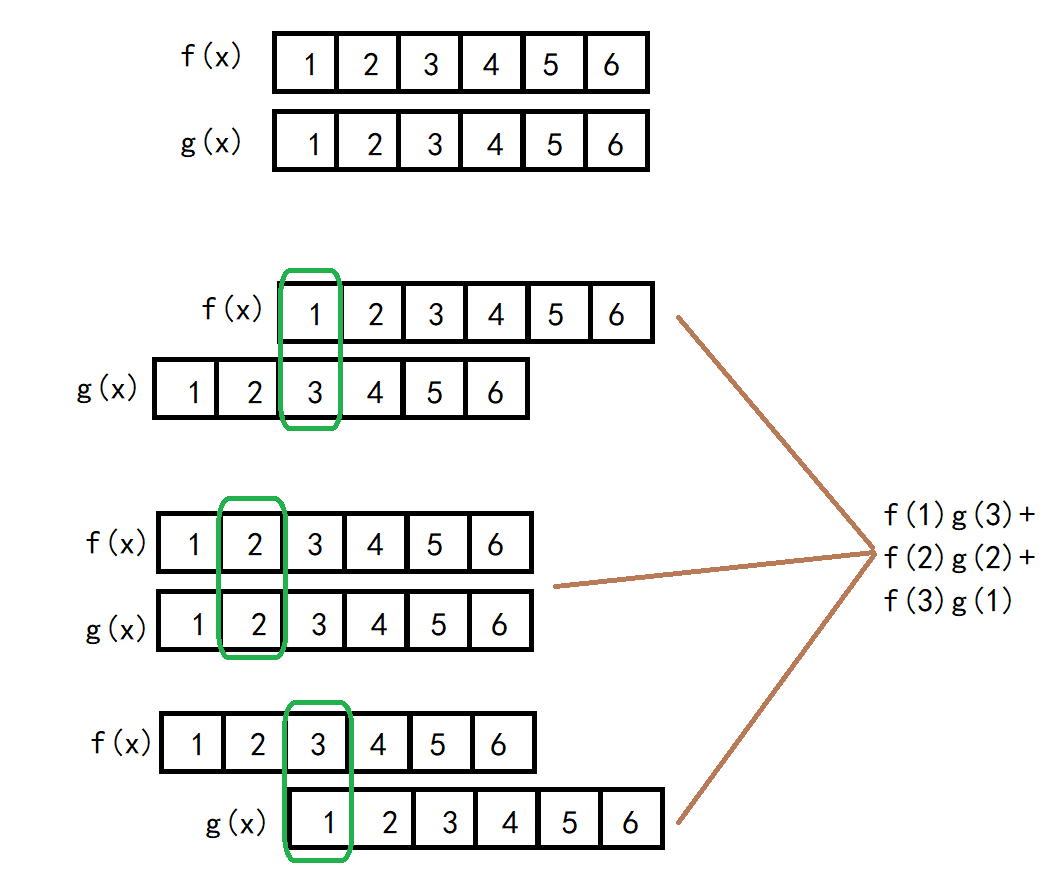
那么这样的概率就是f(1)*g(3)+f(2)*g(2)+f(3)*g(1)符合:
$$ (f * g)(4)=\sum_{m=1}^{3} f(4-m) g(m) $$
下面这张图可以很好的帮助理解卷积：
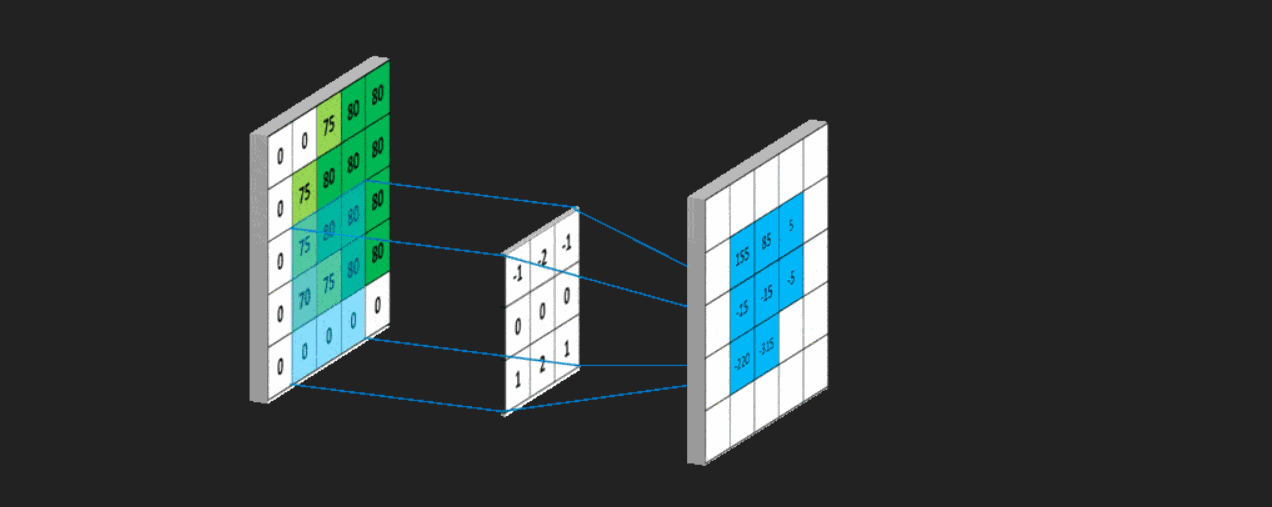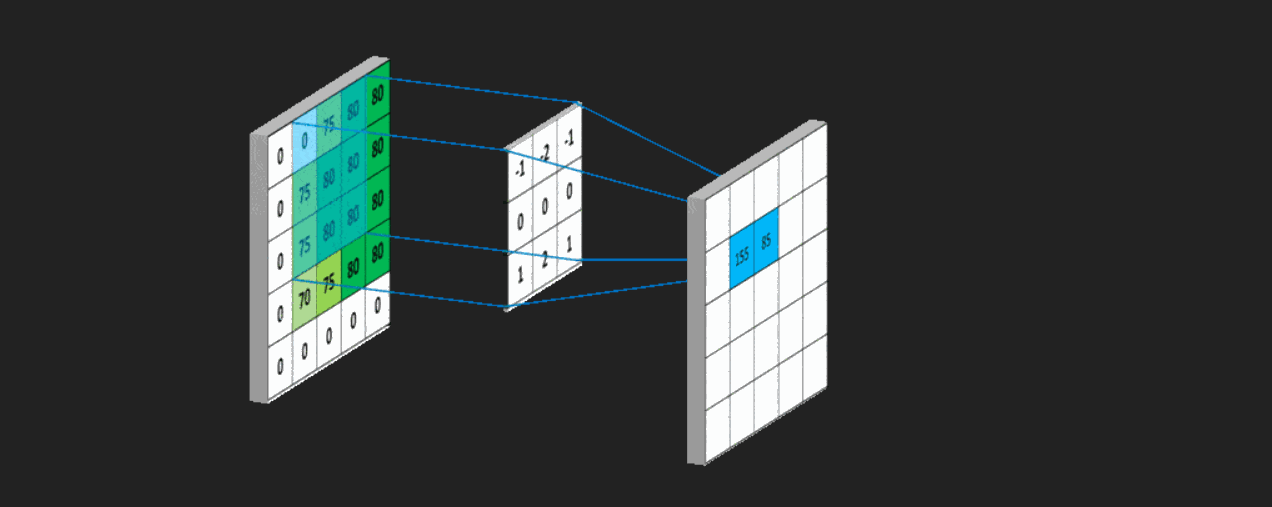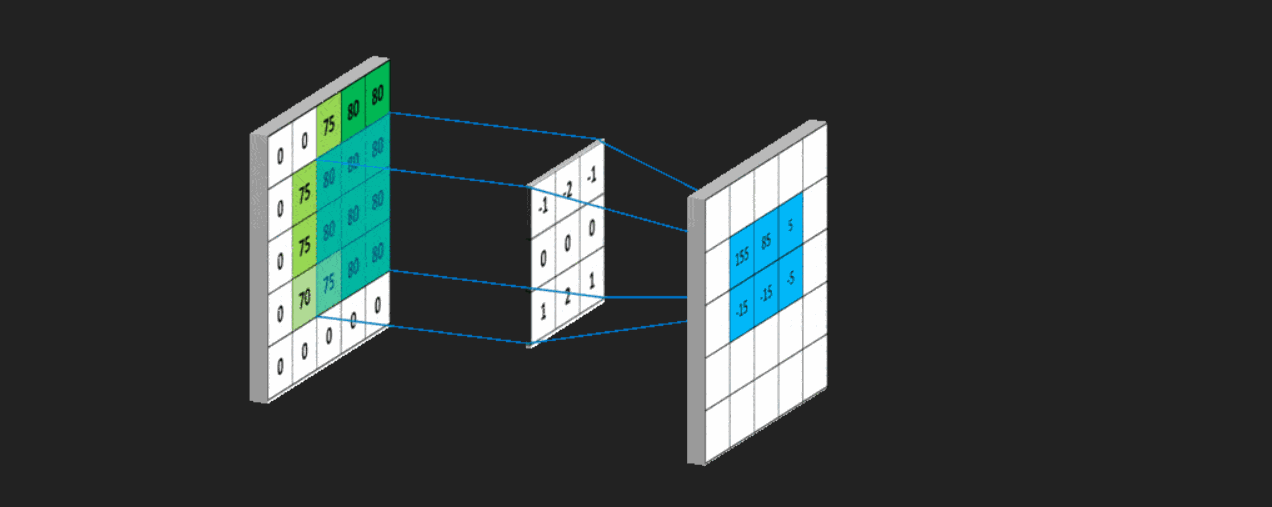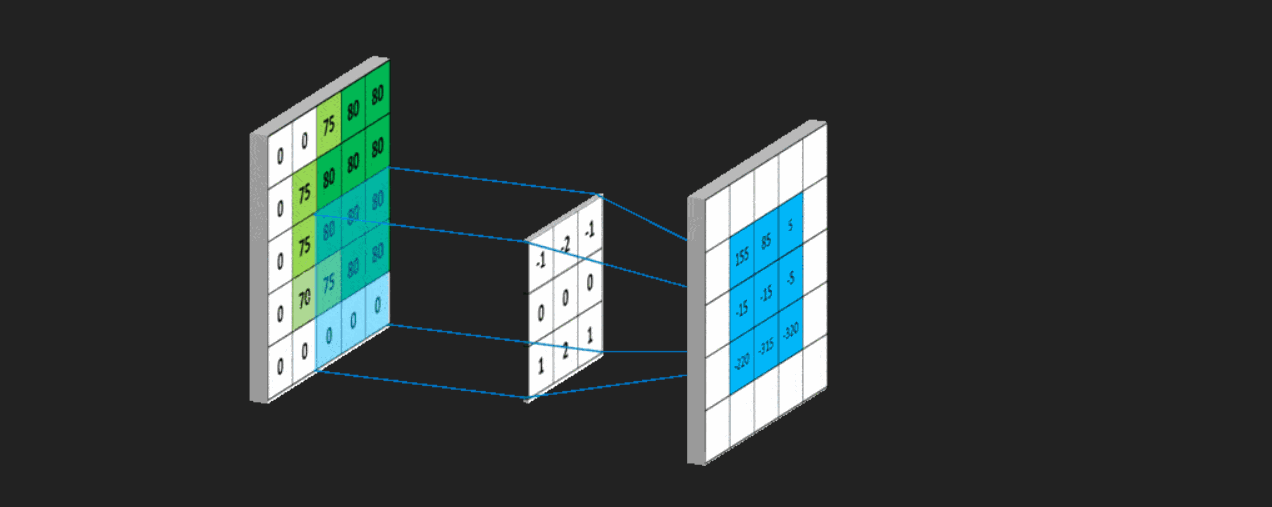
用一个模板和一幅图像进行卷积，对于图像上的一个点，让模板的原点和该点重合，然后模板上的点和图像上对应的点相乘，然后各点的积相加，就得到了该点的卷积值。对图像上的每个点都这样处理。由于大多数模板都是对称的，所以模板不旋转。卷积是一种积分运算，用来求两个曲线重叠区域面积。可以看作加权求和，可以用来消除噪声、特征增强。
把一个点的像素值用它周围的点的像素值的加权平均代替。 卷积是一种线性运算,图像处理中常见的mask运算都是卷积，广泛应用于图像滤波。 卷积关系最重要的一种情况，就是在信号与线性系统或数字信号处理中的卷积定理。利用该定理，可以将时间域或空间域中的卷积运算等价为频率域的相乘运算，从而利用FFT等快速算法，实现有效的计算，节省运算代价。
卷积核
这个核本质上是一个大小固定，由数值参数构成的数组，数组的标定点通常位于数组的中心。数组的大小被称为核支撑。单就技术而言，核支撑实际上仅仅由核数组的非零部分组成。 上图中不停移动的白色块变是卷积核！
卷积函数：cvFilter2D、filter2D()
cvFilter2D()
opencv中的c语言函数，参数如下：
src：输入图像. dst：输出图像. kernel：卷积核, 单通道浮点矩阵. 如果想要应用不同的核于不同的通道，先用 cvSplit 函数分解图像到单个色彩通道上，然后单独处理。 anchor：核的锚点表示一个被滤波的点在核内的位置。 锚点应该处于核内部。缺省值 (-1, -1) 表示锚点在核中心。 函数 cvFilter2D 对图像进行线性滤波，支持 In-place 操作。当核运算部分超出输入图像时，函数从最近邻的图像内部象素差值得到边界外面的象素值。
1void cvFilter2D( const CvArr* src, CvArr* dst,
2 const CvMat* kernel,
3 CvPoint anchor = cvPoint(-1,-1));
filter2D()
opencv中的c++函数，参数如下：
InputArray src: 输入图像 OutputArray dst: 输出图像，和输入图像具有相同的尺寸和通道数量 int ddepth: 目标图像深度，如果没写将生成与原图像深度相同的图像。原图像和目标图像支持的 当ddepth输入值为-1时，目标图像和原图像深度保持一致 InputArray kernel: 卷积核(或者是相关核), 一个单通道浮点型矩阵。如果想在图像不同的通道使用不同的kernel，可以先使用split()函数将图像通道事先分开 Point anchor: 内核的基准点(anchor)，其默认值为(-1, -1)说明位于kernel的中心位置。基准点即kernel中与进行处理的像素点重合的点 double delta: 在储存目标图像前可选的添加到像素的值，默认值为0 int borderType: 像素向外逼近的方法，默认值是BORDER_DEFAULT,即对全部边界进行计算。 该函数使用于任意线性滤波器的图像，支持就地操作。当其中心移动到图像外，函数可以根据指定的边界模式进行插值运算。函数实质上是计算kernel与图像的相关性而不是卷积!
1CV_EXPORTS_W void filter2D( InputArray src, OutputArray dst, int ddepth,
2 InputArray kernel, Point anchor=Point(-1,-1),
3 double delta=0, int borderType=BORDER_DEFAULT );
原理
对于图像的每一个像素点，计算它的邻域像素和滤波器矩阵的对应元素的乘积，然后加起来，作为该像素位置的值，这样就完成了滤波过程！
卷积与相关
对图像和滤波矩阵进行逐个元素相乘再求和的操作就相当于将一个二维的函数移动到另一个二维函数的所有位置，这个操作就叫卷积或者相关。卷积和相关的差别是，卷积需要先对滤波矩阵进行180的翻转，但如果矩阵是对称的，那么两者就没有什么差别了。 图像卷积操作的本质是矩阵卷积。某些特殊的卷积核会使图像产生特殊的效果：
图像处理
下面把均把相关性计算看成是卷积运算，从本质上来说其实就是卷积运算，相当于把矩阵旋转了180°所以看成是卷积！
边缘检测卷积核
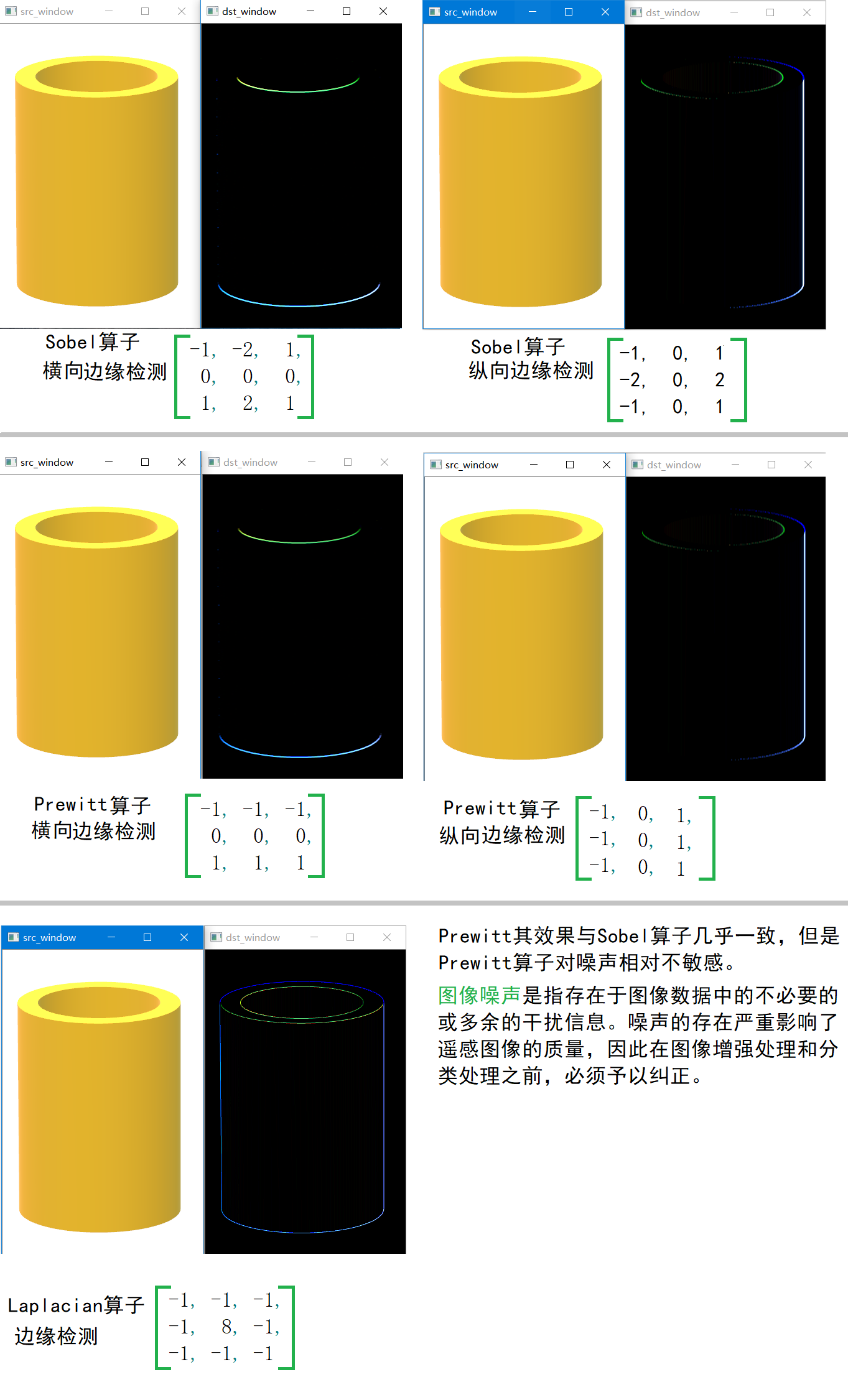
图像锐化卷积核
图像的锐化和边缘检测很像，首先找到边缘，然后把边缘加到原来的图像上面，这样就强化了图像的边缘，使图像看起来更加锐利了。这两者操作统一起来就是锐化滤波器了，也就是在边缘检测滤波器的基础上，再在中心的位置加1，这样滤波后的图像就会和原始的图像具有同样的亮度了，但是会更加锐利。
更加强调边缘的卷积核
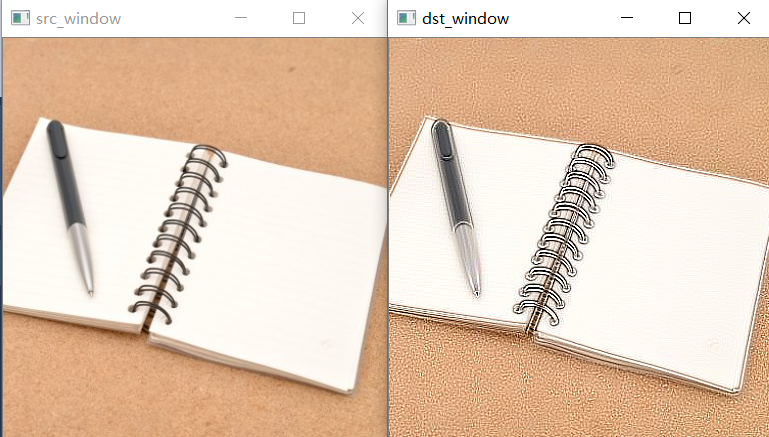
浮雕效果的卷积核
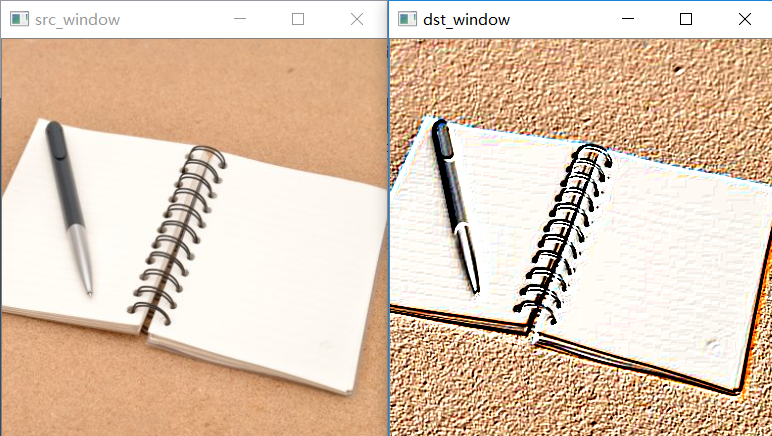
模糊图像的卷积核
Smooth/Blur 是图像处理中最简单和常用的操作之一，使用该操作的原因之一就为了给图像预处理时候减低噪声，使用Smooth/Blur操作其背后是数学的卷积计算
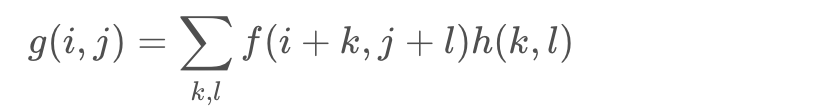
卷积过程：6x6上面是个3x3的窗口，从左向右，从上向下移动，黄色的每个像个像素点值之和取平均值赋给中心红色像素作为它卷积处理之后新的像素值。每次移动一个像素格。
归一化滤波（均值滤波）
$$ k=\frac{1}{\left(k_{\text {width }} * k_{\text {width }}\right)}\left[\begin{array}{ccccc} 1 & 1 & 1 & \ldots & 1 \\ 1 & 1 & 1 & \ldots & 1 \\ 1 & 1 & 1 & \ldots & 1 \\ 1 & 1 & 1 & \ldots & 1 \\ \ldots & \ldots & \ldots & \ldots & 1 \\ 1 & 1 & 1 & \ldots & 1 \end{array}\right] $$
高斯滤波
$$ G_{0}(x, y)=A e *\left(\frac{-\left(x-\mu_{X}\right)^{2}}{2 \sigma_{X}^{2}}+\frac{-\left(\mathrm{y}-\mu_{y}\right)^{2}}{2 \sigma_{y}^{2}}\right) $$
均值模糊
1blur(Mat src, Mat dst, Size(xradius, yradius), Point(-1,-1));
高斯模糊 $$ dst(x, y)=\sum_{0 \leq x<\text { ker nel.cols }} \text { kernel }(x, y) * \operatorname{src}\left(x+x^{1}-\text { anchor. } x, y+y^{1}-\text { anchor.y }\right) $$
1GaussianBlur(Mat src, Mat dst, Size(11, 11), sigmax, sigmay);
其中Size（x, y）, x, y 必须是正数而且是奇数
1#include <iostream>
2#include <opencv2\opencv.hpp>
3
4using namespace cv;
5using namespace std;
6
7int main(int argc, char *argv[]) {
8 Mat src = imread("C:\\Users\\Tim\\Desktop\\Image\\book.png");
9
10 namedWindow("src_window", CV_WINDOW_AUTOSIZE);
11 imshow("src_window", src);
12
13 Mat dst = Mat::zeros(src.size(), src.type());
14
15 //定义卷积核
16
17 //边缘检测
18 //Mat C = (Mat_<double>(3, 3) << -1, -2, -1, 0, 0, 0, 1, 2, 1); // Sobel算子 横向边缘检测
19 //Mat C = (Mat_<double>(3, 3) << -1, 0, 1, -2, 0, 2, -1, 0, 1); // Sobel算子 纵向边缘检测
20 //Mat C = (Mat_<double>(3, 3) << -1, -1, -1, 0, 0, 0, 1, 1, 1); // Prewitt算子 横向边缘检测
21 //Mat C = (Mat_<double>(3, 3) << -1, 0, 1, -1, 0, 1, -1, 0, 1); // Prewitt算子 纵向边缘检测
22 //Mat C = (Mat_<double>(3, 3) << -1, -1, -1, -1, 8, -1, -1, -1, -1); // Laplacian算子 边缘检测
23
24 //图像锐化
25 //Mat C = (Mat_<double>(3, 3) << -1, -1, -1, -1, 9, -1, -1, -1, -1);
26 //Mat C = (Mat_<double>(3, 3) << 1, 1, 1, 1, -7, 1, 1, 1, 1);//更加强调边缘的锐化
27
28 //浮雕
29 //Mat C = (Mat_<double>(3, 3) << -6, -3, 0, -3, 1, 3, 0, 3, 6);
30 filter2D(src, dst, src.depth(), C, Point(-1, -1));
31
32 namedWindow("dst_window", CV_WINDOW_AUTOSIZE);
33 imshow("dst_window", dst);
34
35 moveWindow("src_window", 1, 1);
36 moveWindow("dst_window", 1, 1);
37 waitKey(0);
38 return 0;
39}
1#include <iostream>
2#include <opencv2\opencv.hpp>
3
4using namespace cv;
5using namespace std;
6
7int main(int argc, char *argv[]){
8
9 //Mat src = imread("C:\\Users\\Tim\\Desktop\\Image\\a.jpg");
10 Mat src = imread("C:\\Users\\Tim\\Desktop\\test.png");
11 if (src.empty()){
12 cout << "load image filed..." << endl;
13 return -1;
14 }
15
16 namedWindow("src_window", CV_WINDOW_AUTOSIZE);
17 imshow("src_window", src);
18
19 namedWindow("dst_window", CV_WINDOW_AUTOSIZE);
20 Mat dst;
21 //3*3均值滤波模糊
22 blur(src, dst, Size(3, 3), Point(-1, -1));
23 //GaussianBlur(src, dst, Size(3, 3), 11, 11);//高斯滤波
24 imshow("dst_window", dst);
25 waitKey(0);
26 return 0;
27}
中值滤波
中值滤波对椒盐噪声有很好的抑制作用 椒盐噪声也称为脉冲噪声，是图像中经常见到的一种噪声，它是一种随机出现的白点或者黑点，可能是亮的区域有黑色像素或是在暗的区域有白色像素（或是两者皆有）。盐和胡椒噪声的成因可能是影像讯号受到突如其来的强烈干扰而产生、类比数位转换器或位元传输错误等。例如失效的感应器导致像素值为最小值，饱和的感应器导致像素值为最大值。
- 中值滤波器 中值滤波器（Median filtering） 如其名所隐含的，它将一个像素的值用该像素邻域中强度值的中间值来取代（计算中间值的过程中，也会将该像素的原始值包含），中值滤波器在处理盐和胡椒噪声上能提供绝佳的噪声降低效能。
- 伪中值滤波器 为了改进中值滤波器的计算速率，伪中值滤波器（Pseudo-median filtering） 以近似的方法算出中间值。
-
双边滤波
-
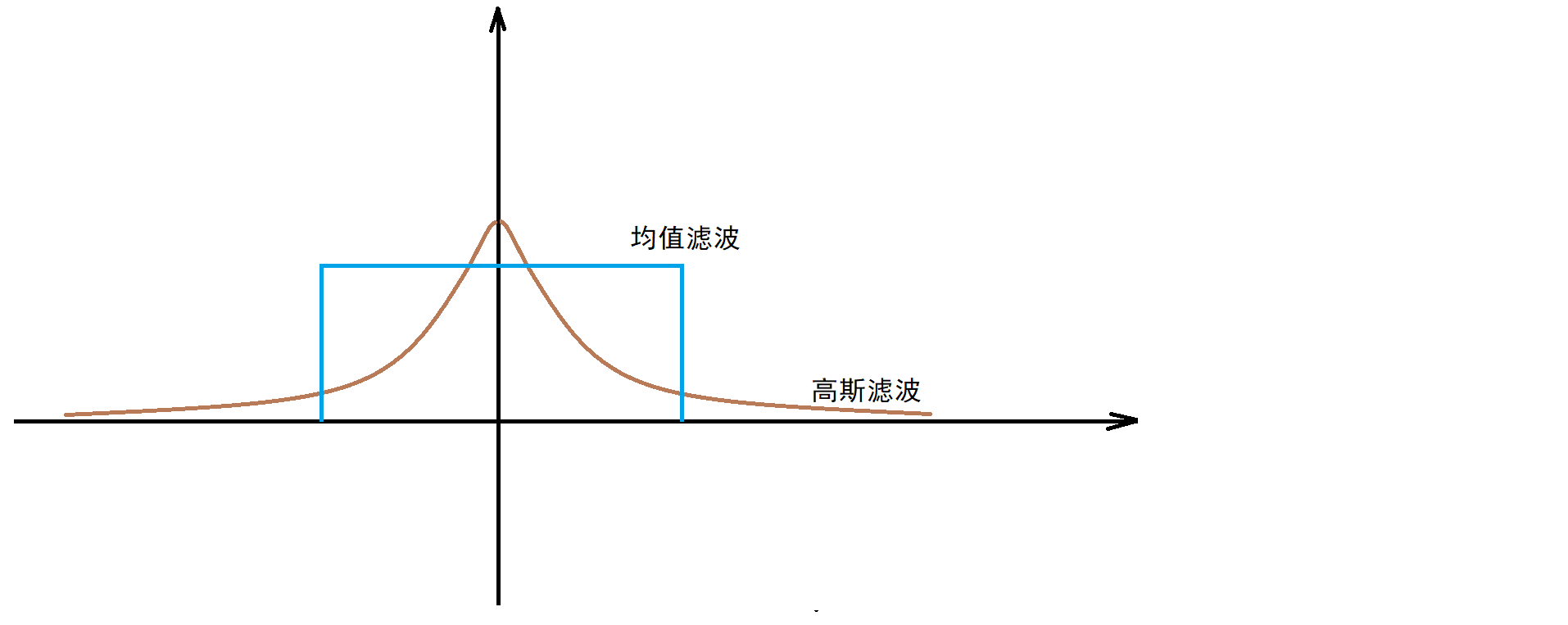
均值模糊无法克服边缘像素信息丢失缺陷。原因是均值滤波是基于平均权重
-
高斯模糊部分克服了该缺陷，但是无法完全避免，因为没有考虑像素值的不同
-
高斯双边模糊 – 是边缘保留的滤波方法，避免了边缘信息丢失，保留了图像轮廓不变
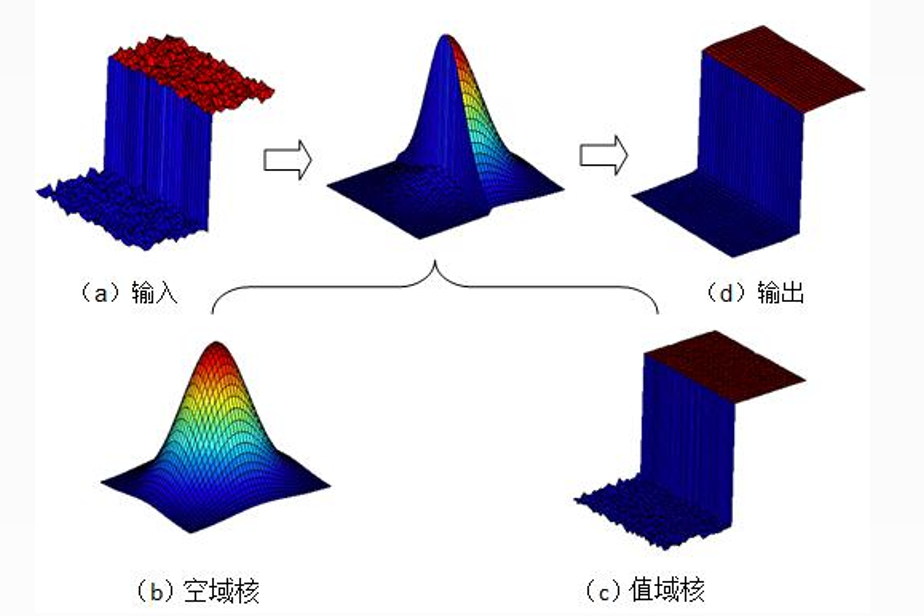
双边滤波就是在对像素进行卷积时，不单单用位置（定义域）信息，还要用到值域信息。你看看高斯卷积的模板，就能明白什么是位置信息。值域信息就是当前像素与邻域像素的差别，差别越大（也就是边界位置），权重越小，这个小权重施加到高斯模板上，就会让高斯权重变小，模糊变弱，也就起到了在边界处弱化高斯模糊的作用，双边滤波的保边作用就是这样实现的。而在平坦区域，值域与领域像素差别小，几乎为零（指数函数用到了），那么权重最大接近1，施加到高斯权重上几乎对高斯不起作用，也就是在平坦区实际执行的就是高斯滤波。 计算公式如下： $$ \mathrm{g}(i, j)=\frac{\sum_{k, l} f(k, l) \omega(i, j, k, l)}{\sum_{k, l} \omega(i, j, k, l)} $$
其中$w(i,j,k,l)$的计算方法如下: $$ \begin{array}{c} d(i, j, k, l)=\exp \left(-\frac{(i-k)^{2}+(j-l)^{2}}{2 \sigma_{d}^{2}}\right) \\ r(i, j, k, l)=\exp \left(-\frac{|f(i, j)-f(k-l)|^{2}}{2 \sigma_{r}^{2}}\right) \\ r(i, j, k, l)=\exp \left(-\frac{(i-k)^{2}+(j-l)^{2}}{2 \sigma_{d}^{2}}-\frac{|f(i, j)-f(k-l)|^{2}}{2 \sigma_{r}^{2}}\right) \end{array} $$
d函数是根据像素距离选择权重，距离越近权重越大，这一点和方框滤波，高斯滤波方式相同。而r函数则是根据像素的差异来分配权值。如果两个像素值越接近，即使相距较远，也比差异大而距离近的像素点权重大。正是r函数的作用，使得边缘，即相距近但差异大的像素点的特性得以保留!
模糊相关函数
中值模糊medianBlur（Mat src, Mat dest, ksize） 双边模糊bilateralFilter(src, dest, d=15, 150, 3); 5 –计算的半径，半径之内的像数都会被纳入计算，如果提供-1 则根据sigma space参数取值 50 – sigma color 决定多少差值之内的像素会被计算 3 – sigma space 如果d的值大于0则声明无效，否则根据它来计算d值 中值模糊的ksize大小必须是大于1而且必须是奇数。
1#include <iostream>
2#include <opencv2\opencv.hpp>
3
4using namespace cv;
5using namespace std;
6
7int main(int argc, char **argv)
8{
9
10 Mat src = imread("C:\\Users\\Tim\\Desktop\\Image\\notbeautify1.png");
11 //Mat src = imread("C:\\Users\\Tim\\Desktop\\Image\\AI.png");
12
13 Mat dst;
14 if (src.empty())
15 {
16 cout << "load image filed..." << endl;
17 return -1;
18 }
19
20 namedWindow("src_window", CV_WINDOW_AUTOSIZE);
21 imshow("src_window", src);
22
23
24 //中值滤波去掉椒盐噪声
25 //medianBlur(src, dst, 3);
26
27 //双边滤波
28 bilateralFilter(src, dst, 15, 100, 3);
29 namedWindow("medianBlur_dst", CV_WINDOW_AUTOSIZE);
30 imshow("medianBlur_dst", dst);
31
32
33 Mat gblur;
34 GaussianBlur(src, gblur, Size(15, 15), 3, 3);
35 namedWindow("HelloWorld",CV_WINDOW_AUTOSIZE);
36 namedWindow("bglur_dst", CV_WINDOW_AUTOSIZE);
37 imshow("bglur_dst", gblur);
38
39 //通过掩模提升对比度
40 Mat retImg;
41 Mat kernal = (Mat_<int>(3, 3) << 0, -1, 0, -1, 5, -1, 0, -1, 0);
42 filter2D(dst, retImg, dst.depth(), kernal, Point(-1, -1), 0);
43
44 namedWindow("retImg", CV_WINDOW_AUTOSIZE);
45 imshow("retImg", retImg);
46
47 waitKey(0);
48 return 0;
49}
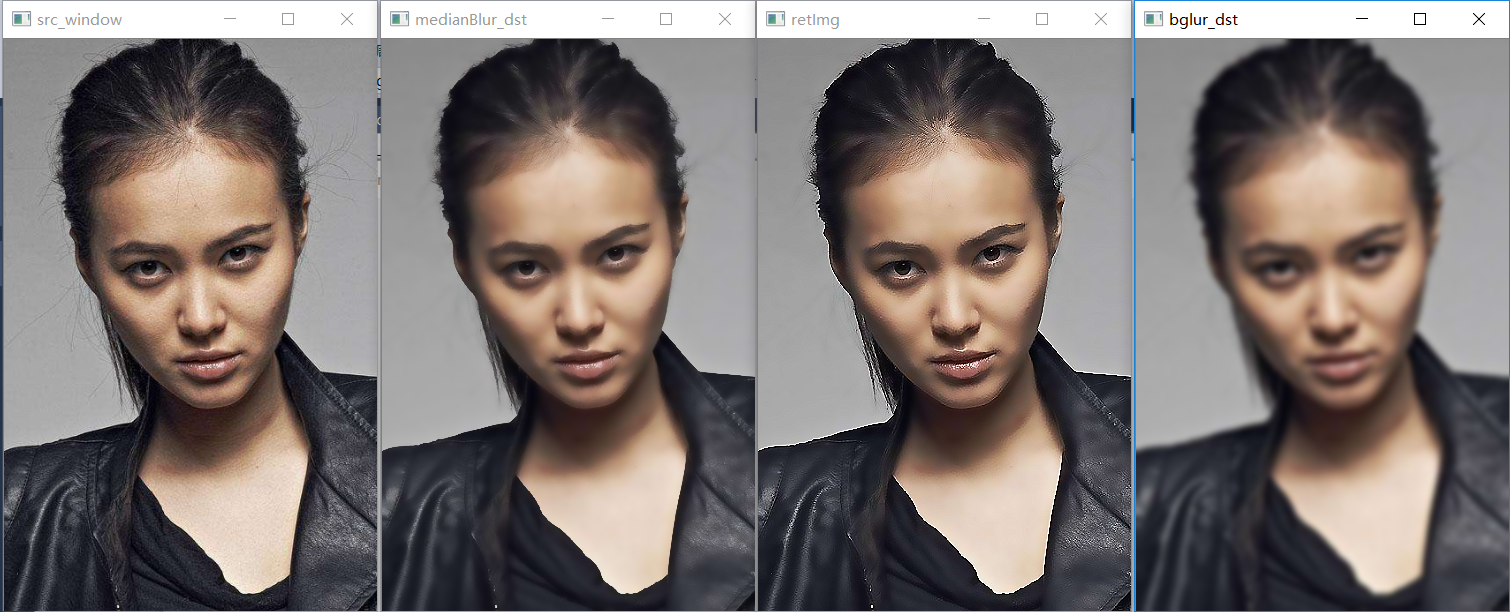
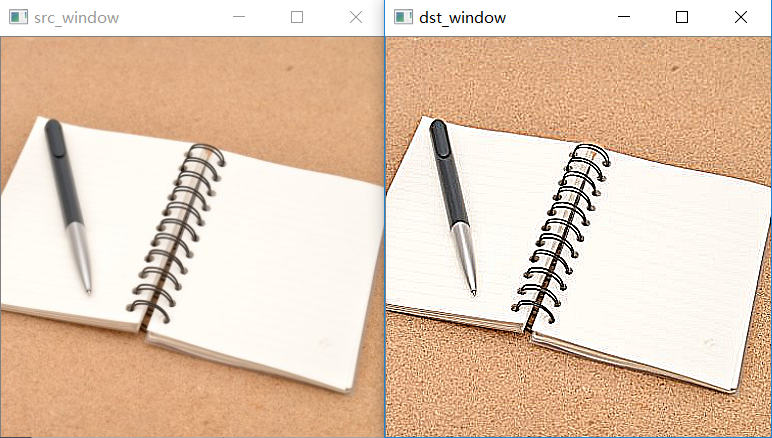
下面经过上述各种滤波器处理之后的效果：
