最近通过代码控制Canvas的旋转的时候， 用到了Quaternion表示旋转，这是一种四元数表示方法，Quaternion的内部属性eulerAngles即时旋转的欧拉角表示方式。本文记录一下四元数、欧拉角、旋转矩阵的概念，旋转矩阵的推导过程，以及他们之间的相互转换方式。

旋转矩阵

2D的旋转矩阵

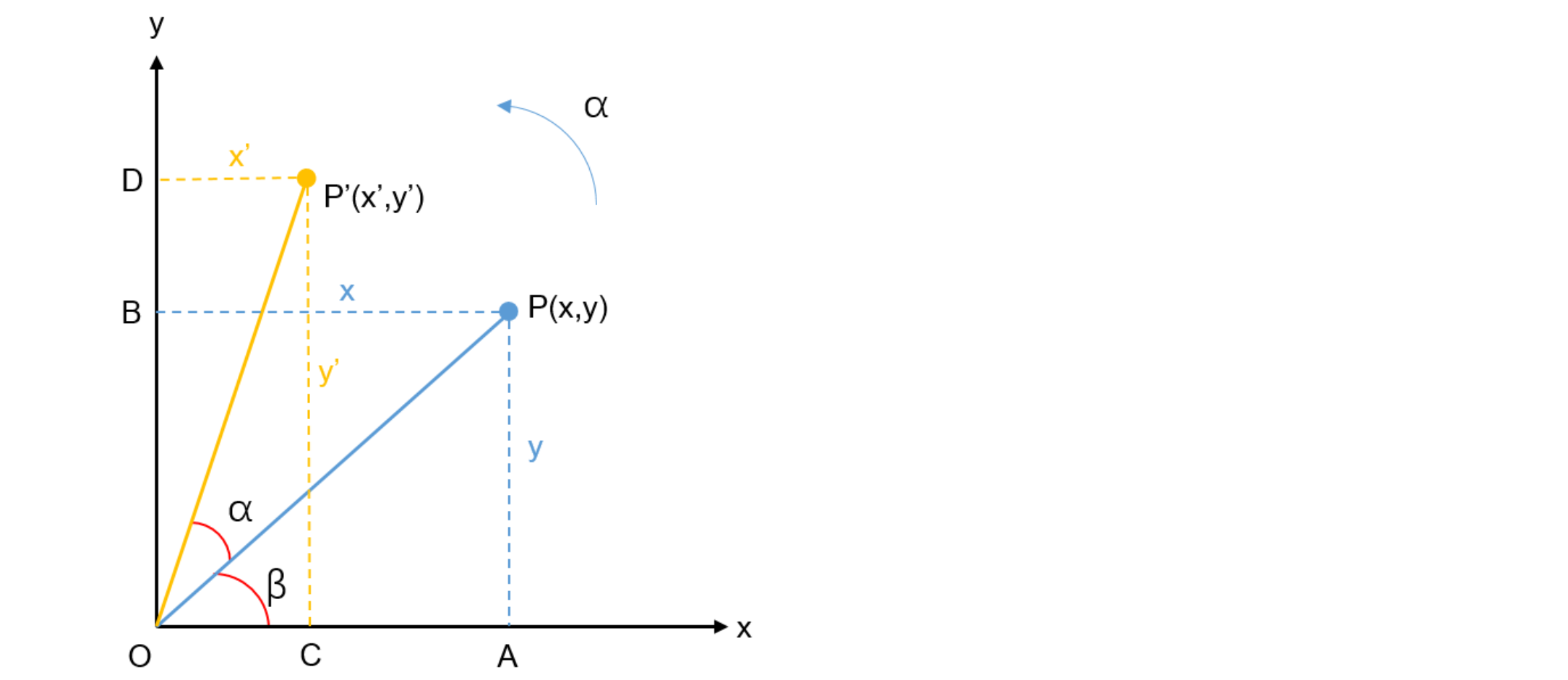
如图所示，2D空间中的旋转：假设点 P从 $(x, y)$ 旋转到 P' $(x', y')$，旋转角度是α，P 与 P' 点对应的X、Y轴上的点分别是 A B C D。另外这是一个旋转操作，所以 OP = OP' 设其长度为r。则 $r=\sqrt{x^{2}+y^{2}}$

对于三角形OPA有：

$$\begin{matrix} cos\beta=\frac{x}{r} \ sin\beta=\frac{y}{r} \end{matrix}$$

即可推导出：

$$\begin{matrix} x=rcos\beta \ y=rsin\beta \end{matrix}$$

对于$x'$ 、$y'$，根据上面已知条件，可以使用如下方式表示：

$$\begin{matrix} x^{'}=r\cdot cos(\alpha+\beta)\ =r\cdot (cos\alpha cos\beta-sin\alpha sin\beta)\ =cos\alpha cos\beta\cdot r-sin\alpha sin\beta \cdot r\ =cos\alpha \cdot x -sin\alpha \cdot y \end{matrix}$$

$$\begin{matrix} y^{'}=r\cdot sin(\alpha+\beta)\ =r\cdot (sin\alpha cos\beta+cos\alpha sin\beta)\ =sin\alpha cos\beta\cdot r+cos\alpha sin\beta \cdot r\ =sin\alpha \cdot x +cos\alpha \cdot y \end{matrix}$$

将上面的式子写成矩阵相乘的形式如下

$$\left[\begin{matrix} x^{'}\ y^{'} \end{matrix}\right]=\left[\begin{matrix} cos\alpha & -sin\alpha\ sin\alpha & cos\alpha \end{matrix}\right]\left[\begin{matrix} x\ y \end{matrix}\right]$$

这个公式便是二维平面内旋转前后的坐标关系的矩阵乘法表示形式。

3D的旋转矩阵

在推得上面2D旋转的公式之后，3D旋转公式就相对简单了。例如某个点绕Z轴旋转α角，也就是说旋转后的Z坐标是不变的，变化的只是x、y坐标。因此甚至可以基于2D公式，不用推导的写出下面这个式子，因为为了满足相等关系，必须补充系数矩阵元素:

$$\left[\begin{matrix} x^{'}\ y^{'}\ z \end{matrix}\right]=\left[\begin{matrix} cos\alpha & -sin\alpha & 0\ sin\alpha & cos\alpha & 0\ 0 & 0 & 1 \end{matrix}\right]\left[\begin{matrix} x\ y\ z \end{matrix}\right]$$

而这个式子中的系数矩阵可以记为如下形式：

$$R_{Z}(\alpha)=\left[\begin{matrix} cos\alpha & -sin\alpha & 0\ sin\alpha & cos\alpha & 0\ 0 & 0 & 1 \end{matrix}\right]$$

这里的R就是旋转矩阵。同时依据绕哪个轴旋转其坐标不变这个性质可以从形式上很快写出绕X、Y轴的旋转矩阵：

$$R_{X}(\alpha)=\left[\begin{matrix} 1 & 0 & 0\ 0 & cos\alpha & -sin\alpha\ 0 & sin\alpha & cos\alpha \end{matrix}\right]$$

$$R_{Y}(\alpha)=\left[\begin{matrix} cos\alpha & 0 & sin\alpha\ 0 & 1 & 0\ -sin\alpha & 0 & cos\alpha \end{matrix}\right]$$

欧拉角

没错，欧拉角之所以叫做欧拉角确实就是因为这是数学家欧拉提出来的！

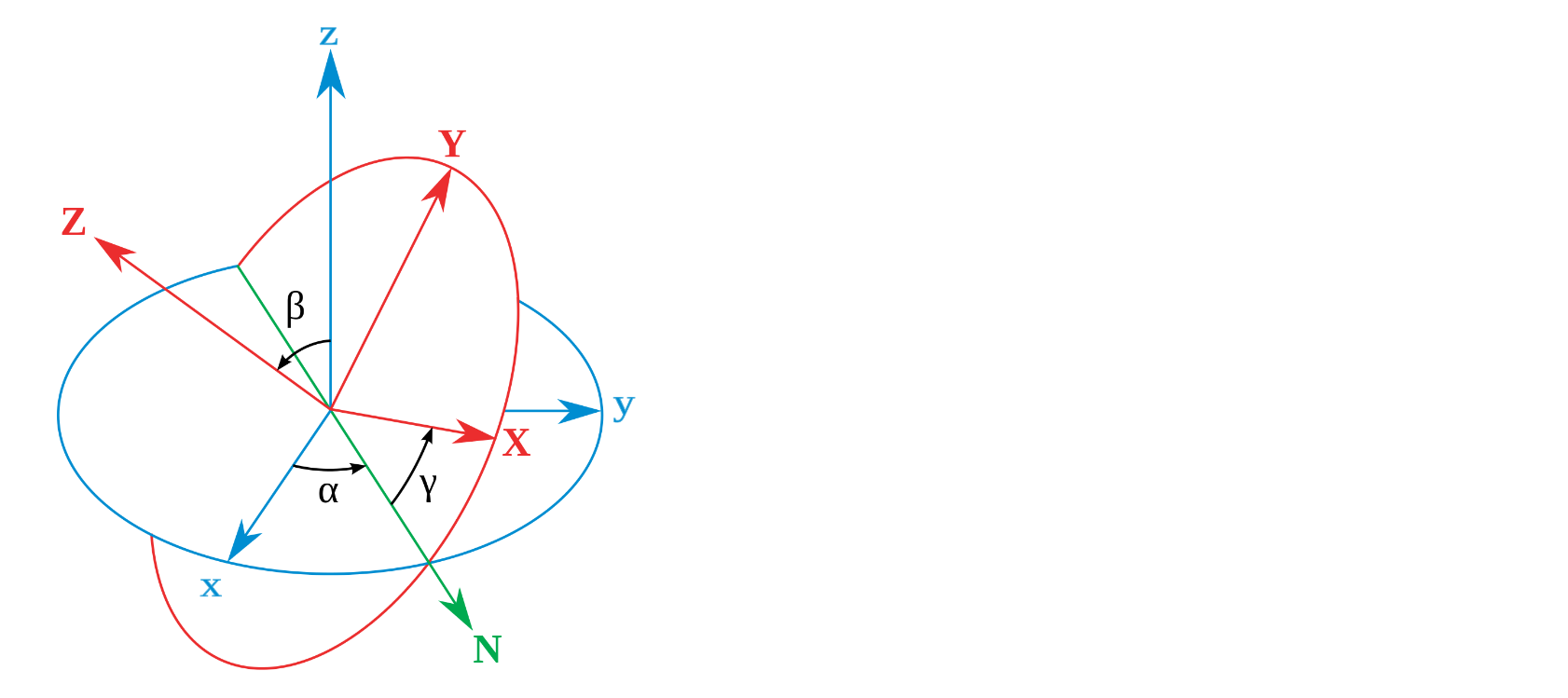
对于在三维空间里的一个参考系，任何坐标系的取向，都可以用三个欧拉角来表现。

对于夹角的顺序和标记，夹角的两个轴的指定，并没有任何常规。每当用到欧拉角时，我们必须明确的表示出夹角的顺序，指定其参考轴。 所以目前存在两种参考方式：

第一种是绕固定参考坐标轴（这里假设固定参考坐标轴是A）旋转：假设开始两个坐标系重合，先将 B 绕 A 的X轴旋转γ ，然后绕 A 的 Y 轴旋转 β，最后绕 A 的 Z 轴旋转α ，就能旋转到当前姿态。在整个过程中，坐标系 A 都没有发生变动，只是作为参考而已。

另一种姿态描述方式是绕自身坐标轴旋转：先将 B 绕自身的Z轴旋转α，然后绕 Y 轴旋转 β，最后绕 X 轴旋转 γ，就能旋转到当前姿态：

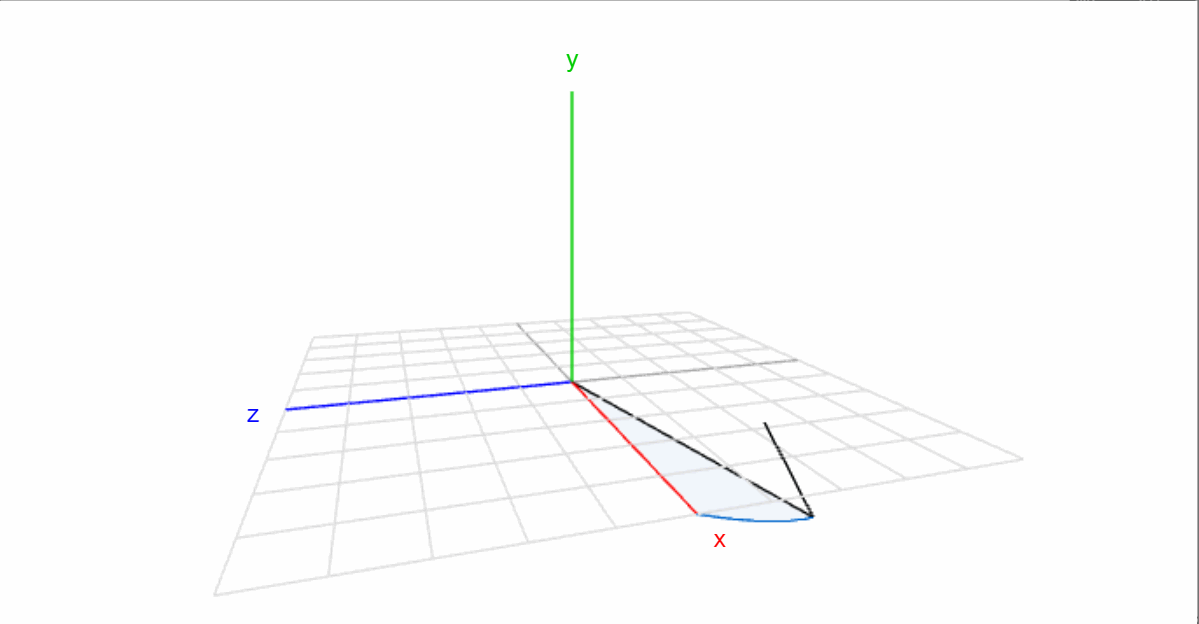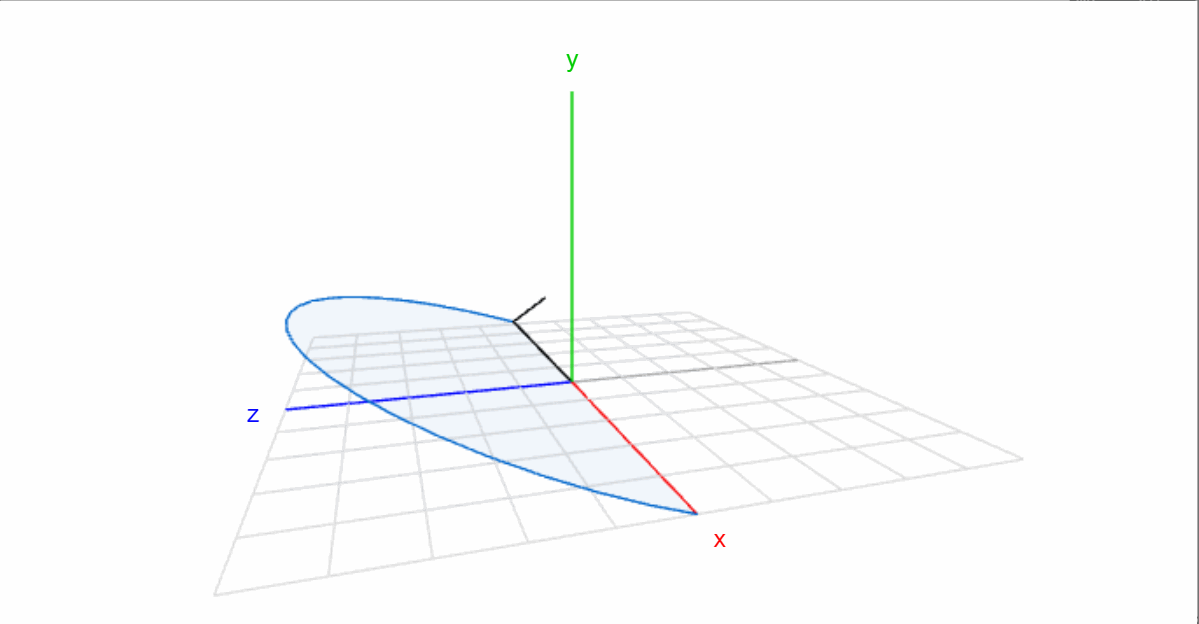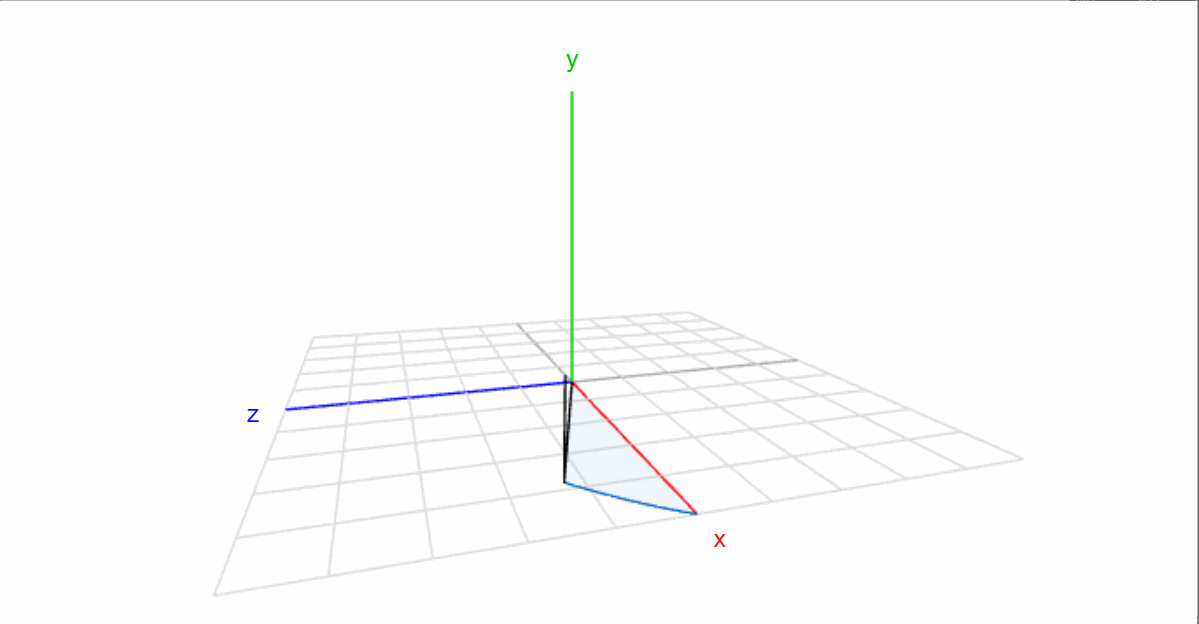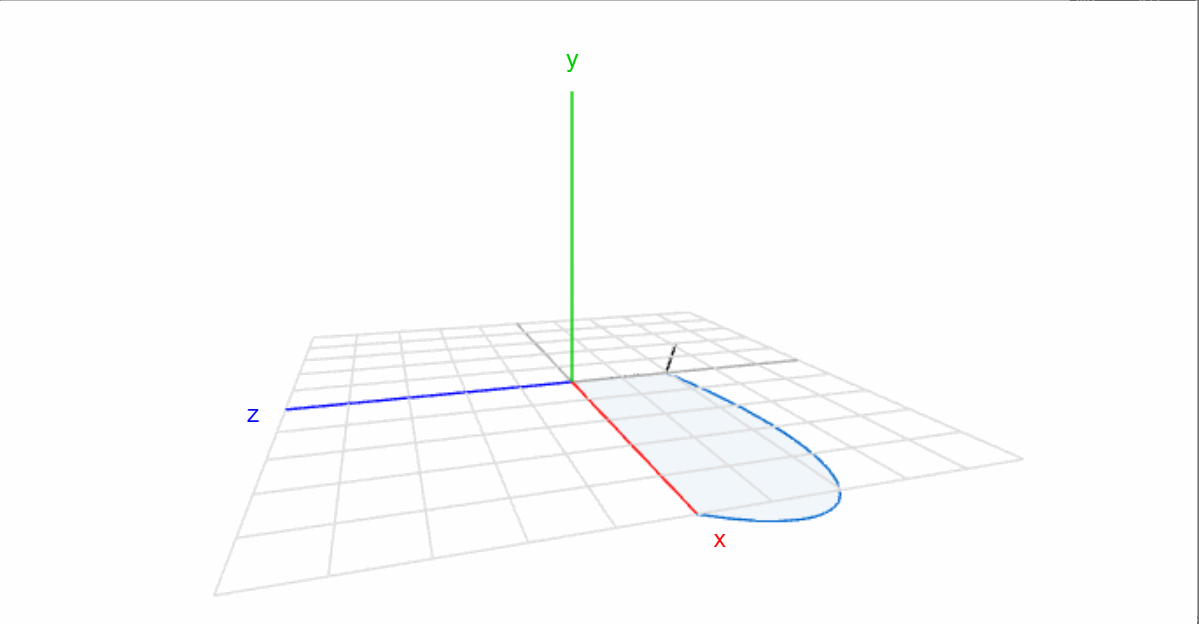
虽然两种旋转方式不同，但可以发现这两种描述方式得到的旋转矩阵是一样的，即绕固定坐标轴X-Y-Z旋转(γ,β,α)和绕自身坐标轴Z-Y-X旋转(α,β,γ)的最终结果一样，只是描述的方法有差别而已。

$$R = R_{Z}(\alpha)R_{Y}(\beta)R_{X}(\gamma)=\left[\begin{matrix} cos\alpha cos\beta & cos\alpha sin\beta sin\gamma - sin\alpha cos\gamma & cos\alpha sin\beta cos\gamma + sin\alpha sin\gamma\ sin\alpha cos\beta & cos\alpha cos\gamma + sin\alpha sin\beta sin\gamma & sin\alpha sin\beta cos\gamma - sin\gamma cos\alpha\ -sin\beta & cos\beta sin\gamma & cos\beta cos\gamma \end{matrix}\right]$$

欧拉角是不可传递的，旋转的顺序影响旋转的结果，不同的应用又可能使用不同的旋转顺序，旋转顺序无法统一，另外欧拉角存在万向节死锁（Gimbal Lock）问题，简单来说和陀螺仪的万向节死锁是一个道理， 是由于欧拉旋转定义本身造成的。这种围绕选旋转前固定轴的先Z、再X、再Y的旋转操作，与其最终所预期的三个轴向可以旋转的结果并非一定是一对一的映射。某些情况下是多对一的映射，造成一些旋转自由度的缺失，也就是死锁。

四元数

在计算机图形学中，四元数用于物体的旋转，是一种较为复杂，但是效率较高的旋转方式。对于一个物体的旋转，其实我们只需要知道四个值：一个旋转的向量 + 一个旋转的角度。而四元数就是这样的设计， 其中x, y, z 代表的是向量的三维坐标，w代表的是角度：

$$q=(x, y, z, w)$$

其实四元数本质上是一个超复数，一个四元数拥有一个实部和三个虚部，三个虚部之间满足如下关系：

$$\mathbf{q}=q_{0}+q_{1} i+q_{2} j+q_{3} k$$

$$ \left{\begin{array}{c} i^{2}=j^{2}=k^{2}=-1 \ i j=k, j i=-k \ j k=i, k j=-i \ k i=j, i k=-j \end{array}\right. $$

$q_{0}$ 对应 w，$q_{1}$、$q_{2}$、$q_{3}$ 分别对应 x y z，那么四元数如何表示旋转呢？如某次旋转是绕某一向量K=(Kx,Ky,Kz)进行了角度为 θ 的旋转，那么利用四元数就可以表示这个旋转：

$$ \begin{array}{c} x=K_{x} \sin \frac{\theta}{2} \ y=K_{y} \sin \frac{\theta}{2} \ z=K_{z} \sin \frac{\theta}{2} \ w=\cos \frac{\theta}{2} \ x^{2}+y^{2}+z^{2}+w^{2}=1 \end{array} $$

转换关系

欧拉角 -> 四元数

将Z-Y-X欧拉角（或RPY角：绕固定坐标系的X-Y-Z依次旋转α, β, γ角）转换为四元数：

$$ \mathbf{q}=\left(\begin{array}{l} q_{0} \ q_{1} \ q_{2} \ q_{3} \end{array}\right)=\left(\begin{array}{l} \cos \left(\frac{\alpha}{2}\right) \cos \left(\frac{\beta}{2}\right) \cos \left(\frac{\gamma}{2}\right)+\sin \left(\frac{\alpha}{2}\right) \sin \left(\frac{\beta}{2}\right) \sin \left(\frac{\gamma}{2}\right) \ \sin \left(\frac{\alpha}{2}\right) \cos \left(\frac{\beta}{2}\right) \cos \left(\frac{\gamma}{2}\right)-\cos \left(\frac{\alpha}{2}\right) \sin \left(\frac{\beta}{2}\right) \sin \left(\frac{\gamma}{2}\right) \ \cos \left(\frac{\alpha}{2}\right) \sin \left(\frac{\beta}{2}\right) \cos \left(\frac{\gamma}{2}\right)+\sin \left(\frac{\alpha}{2}\right) \cos \left(\frac{\beta}{2}\right) \sin \left(\frac{\gamma}{2}\right) \ \cos \left(\frac{\alpha}{2}\right) \cos \left(\frac{\beta}{2}\right) \sin \left(\frac{\gamma}{2}\right)-\sin \left(\frac{\alpha}{2}\right) \sin \left(\frac{\beta}{2}\right) \cos \left(\frac{\gamma}{2}\right) \end{array}\right) $$

 1struct Quaternion
 2{
 3    double w, x, y, z;
 4};
 5 
 6Quaternion ToQuaternion(double yaw, double pitch, double roll) // yaw (Z), pitch (Y), roll (X)
 7{
 8    // Abbreviations for the various angular functions
 9    double cy = cos(yaw * 0.5);
10    double sy = sin(yaw * 0.5);
11    double cp = cos(pitch * 0.5);
12    double sp = sin(pitch * 0.5);
13    double cr = cos(roll * 0.5);
14    double sr = sin(roll * 0.5);
15 
16    Quaternion q;
17    q.w = cy * cp * cr + sy * sp * sr;
18    q.x = cy * cp * sr - sy * sp * cr;
19    q.y = sy * cp * sr + cy * sp * cr;
20    q.z = sy * cp * cr - cy * sp * sr;
21 
22    return q;
23}

欧拉角 -> 旋转矩阵

将Z-Y-X欧拉角（或RPY角：绕固定坐标系的X-Y-Z依次旋转α, β, γ角）转换为矩阵：

$$ R=R_{Z}(\alpha) R_{Y}(\beta) R_{X}(\gamma)=\left(\begin{array}{ccc} \cos \alpha \cos \beta & \cos \alpha \sin \beta \sin \gamma-\sin \alpha \cos \gamma & \cos \alpha \sin \beta \cos \gamma+\sin \alpha \sin \gamma \ \sin \alpha \cos \beta & \cos \alpha \cos \gamma+\sin \alpha \sin \beta \sin \gamma & \sin \alpha \sin \beta \cos \gamma-\sin \gamma \cos \alpha \ -\sin \beta & \cos \beta \sin \gamma & \cos \beta \cos \gamma \end{array}\right) $$

四元数 -> 欧拉角

四元数 $\mathbf{q}=q_{0}+q_{1} i+q_{2} j+q_{3} k$ 到欧拉角的转换为：

$$ \begin{aligned} \alpha &=\arctan \left(\frac{2\left(q_{0} q_{1}+q_{2} q_{3}\right)}{1-2\left(q_{1}^{2}+q_{2}^{2}\right)}\right) \ \beta &=\arcsin \left(2\left(q_{0} q_{2}-q_{1} q_{3}\right)\right) \ \gamma &=\arctan \left(\frac{2\left(q_{0} q_{3}+q_{1} q_{2}\right)}{1-2\left(q_{2}^{2}+q_{3}^{2}\right)}\right) \end{aligned} $$

由于arctan和arcsin的取值范围在−π/2 - π/2之间，只有180°，而绕某个轴旋转时范围是360°，因此要使用atan2函数代替arctan函数。

$$ \begin{array}{l} \alpha=\operatorname{atan} 2\left(2\left(q_{0} q_{1}+q_{2} q_{3}\right), 1-2\left(q_{1}^{2}+q_{2}^{2}\right)\right) \ \beta=\arcsin \left(2\left(q_{0} q_{2}-q_{1} q_{3}\right)\right) \ \gamma=\operatorname{atan} 2\left(2\left(q_{0} q_{3}+q_{1} q_{2}\right), 1-2\left(q_{2}^{2}+q_{3}^{2}\right)\right) \end{array} $$

 1#define _USE_MATH_DEFINES
 2#include <cmath>
 3 
 4struct Quaternion {
 5    double w, x, y, z;
 6};
 7 
 8struct EulerAngles {
 9    double roll, pitch, yaw;
10};
11 
12EulerAngles ToEulerAngles(Quaternion q) {
13    EulerAngles angles;
14 
15    // roll (x-axis rotation)
16    double sinr_cosp = 2 * (q.w * q.x + q.y * q.z);
17    double cosr_cosp = 1 - 2 * (q.x * q.x + q.y * q.y);
18    angles.roll = std::atan2(sinr_cosp, cosr_cosp);
19 
20    // pitch (y-axis rotation)
21    double sinp = 2 * (q.w * q.y - q.z * q.x);
22    if (std::abs(sinp) >= 1)
23        angles.pitch = std::copysign(M_PI / 2, sinp);
24    else
25        angles.pitch = std::asin(sinp);
26 
27    // yaw (z-axis rotation)
28    double siny_cosp = 2 * (q.w * q.z + q.x * q.y);
29    double cosy_cosp = 1 - 2 * (q.y * q.y + q.z * q.z);
30    angles.yaw = std::atan2(siny_cosp, cosy_cosp);
31 
32    return angles;
33}

四元数 ->旋转矩阵

四元数 $\mathbf{q}=q_{0}+q_{1} i+q_{2} j+q_{3} k$ 到欧拉角的转换为：

$$ R=\left(\begin{array}{lll} 1-2\left(q_{2}^{2}+q_{3}^{2}\right) & 2\left(q_{1} q_{2}-q_{0} q_{3}\right) & 2\left(q_{1} q_{3}+q_{0} q_{2}\right) \ 2\left(q_{1} q_{2}+q_{0} q_{3}\right) & 1-2\left(q_{1}^{2}+q_{3}^{2}\right) & 2\left(q_{2} q_{3}-q_{0} q_{1}\right) \ 2\left(q_{1} q_{3}-q_{0} q_{2}\right) & 2\left(q_{2} q_{3}+q_{0} q_{1}\right) & 1-2\left(q_{1}^{2}+q_{2}^{2}\right) \end{array}\right) $$

旋转矩阵 -> 欧拉角

假设旋转矩阵为，要注意的是，旋转顺序必须要是Z、Y、X。

$$ R=\left(\begin{array}{lll} r_{11} & r_{12} & r_{13} \ r_{21} & r_{22} & r_{23} \ r_{31} & r_{32} & r_{33} \end{array}\right) $$

可求出各轴的旋转角为：

$$ \begin{array}{c} \theta_{Z}=\operatorname{atan} 2\left(r_{21}, r_{11}\right) \ \theta_{Y}=\operatorname{atan} 2\left(-r_{31}, \sqrt{r_{31}^{2}+r_{33}^{2}}\right) \ \theta_{X}=\operatorname{atan} 2\left(r_{32}, r_{33}\right) \end{array} $$

旋转矩阵 -> 四元数

假设旋转矩阵为，要注意的是，旋转顺序必须要是Z、Y、X。

$$ R=\left(\begin{array}{lll} r_{11} & r_{12} & r_{13} \ r_{21} & r_{22} & r_{23} \ r_{31} & r_{32} & r_{33} \end{array}\right) $$

其对应的四元数为：

$$ \left{\begin{matrix} q_{0}=\frac{\sqrt{tr(R)+1}}{2}\ q_{1}=\frac{r_{23}-r_{32}}{4q_{0}}\ q_{2}=\frac{r_{31}-r_{13}}{4q_{0}}\ q_{3}=\frac{r_{12}-r_{21}}{4q_{0}} \end{matrix}\right. $$

其中tr(R)表示R矩阵的迹，也即矩阵R的主对角线（从左上方至右下方的对角线）上各个元素的总和。

工程实践

直接去改变Transform的欧拉角显然是不合适的，其结果几乎是不可预测的。但是某些情况下，却是可以预期的，就是你仅仅在一个轴向进动，其它两个轴向保持为0，此时有效，并且直接修改欧拉角的代码效率应该是比较高的，或者想要设置绕X轴的欧拉角设置为0时，可以直接修改欧拉角：

1-- 原始欧拉角
2local eulerV3 = canvas.transform.rotation.eulerAngles
3-- 构造新欧拉角
4canvas.transform.rotation = Quaternion.Euler(0, eulerV3,y, eulerV3.z)

参考资料

https://zh.m.wikipedia.org/zh/欧拉角

https://www.zhihu.com/question/47736315

https://zhuanlan.zhihu.com/p/45404840