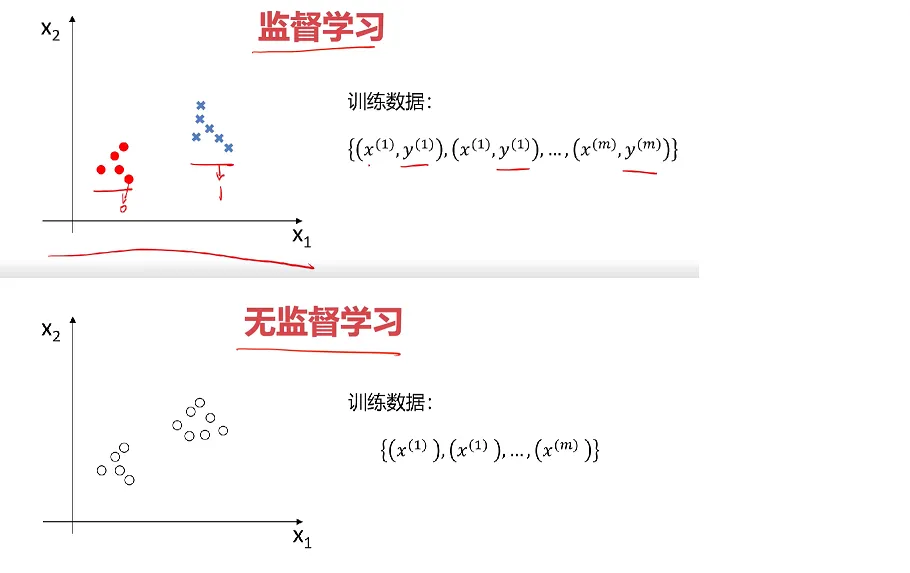
监督式学习：发现数据属性和类别属性之间的关联。并通过利用这些模式用来预测未知数据实例的类别属性。

无监督学习：机器学习的一种方法，没有给定事先标记过的训练示例自动对输入的数据进行分类或分群。

非监督式学习中研究最多、应用最广的是聚类算法（Clustering）。常见的无监督学习应用在聚类分析、关联规则、维度缩减等。聚类算法是机器学习的一种，属于非监督式学习，没有给定事先标记过的训练示例，自动对输入的数据进行分类或分群，所以称之为聚类。

聚类算法的优点：

1、算法不受监督信息(偏见)的约束，可能考虑到新的信息

2、不需要标签数据，极大程度扩大数据样本

无监督式学习与监督式学习区别

聚类分析概念

聚类分析又称为群分析，根据对象某些属性的相似度，将其自动化分为不同的类别。

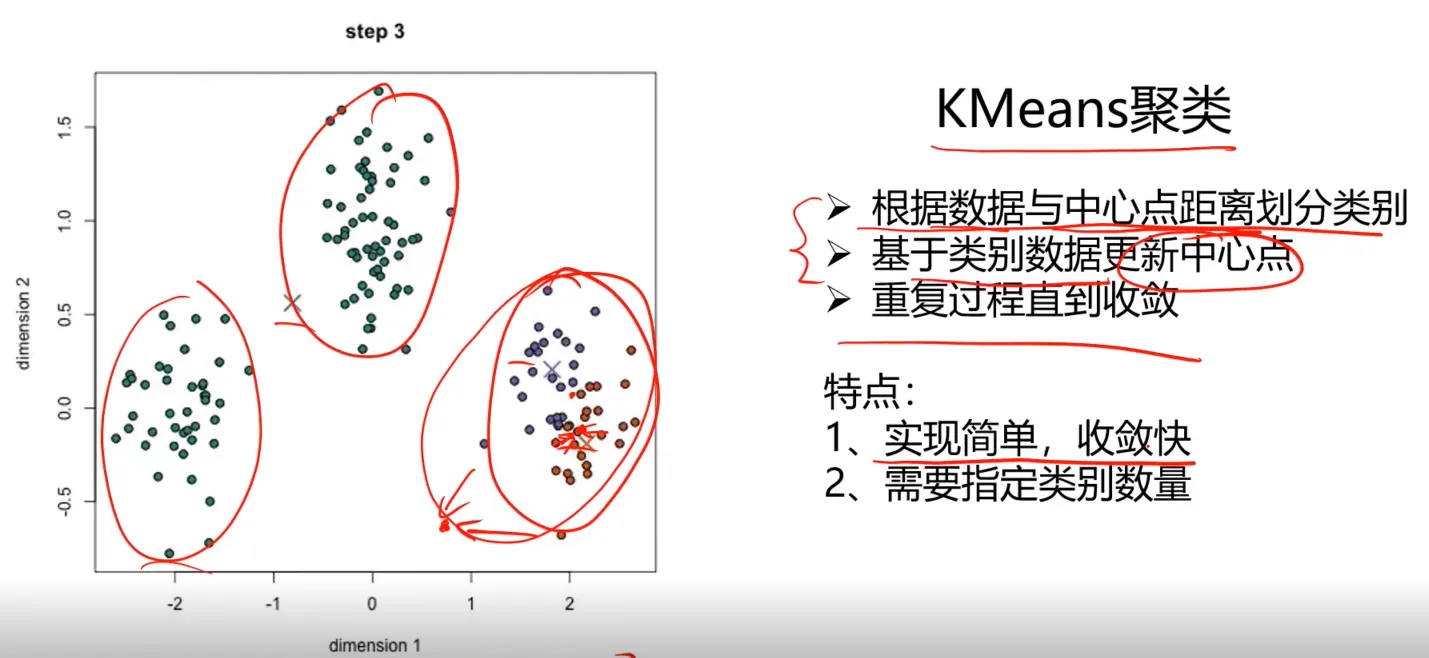
1、KMeans聚类（K均值聚类）

根据数据与中心点距离划分类别

基于类别数据更新中心点

重复过程直到收敛

可以参考下面的动图：

K-均值聚类公式

K-均值算法: 以空间中个点为中心进行聚类，对最靠近他们的对象归类，是聚类算法中最为基础但也最为重要的算法。公式如下：

数据点与各簇中心点距离：$dist(x_i,u_j^t)$

根据距离归类：$x_i\in u_{nearest}^t$

中心点更新：$u_j^{t+1}=\frac{1}{k}\sum_{x_i\in s_j}(x_i)$

其中，$s_j$ 为 t时刻第j个区域簇；k是指包含在$s_j$ 范围内点的个数；$x_i$ 是指包含在包含在$s_j$ 范围内的点 $u_j^{t}$ 表示 t 状态下第i区域的中心。

K-均值算法的算法流程

1、选择聚类的个数k

2、确定聚类中心

3、根据点到聚类中心聚类确定各个点所属类别

4、根据各个类别数据更新聚类中心

5、重复以上步骤直到收敛(中心点不再变化)

:::info{title=“K-均值算法优缺点”} K-均值算法优点: 1、原理简单，实现容易，收敛速度快 2、参数少，方便使用

K-均值算法缺点： 1、必须设置族的数量 2、随机选择初始聚类中心，结果可能缺乏一致性 :::

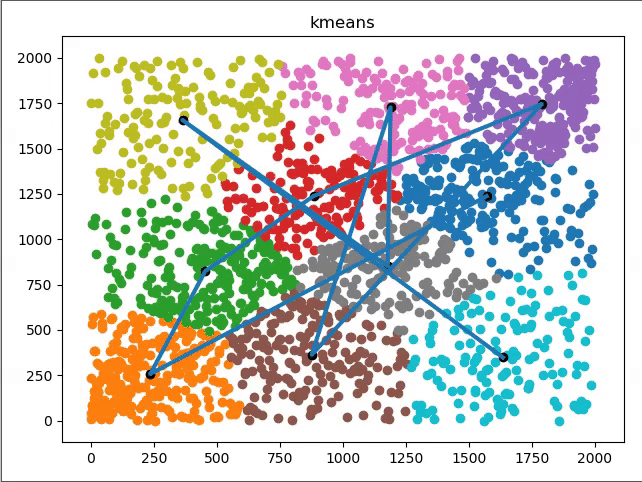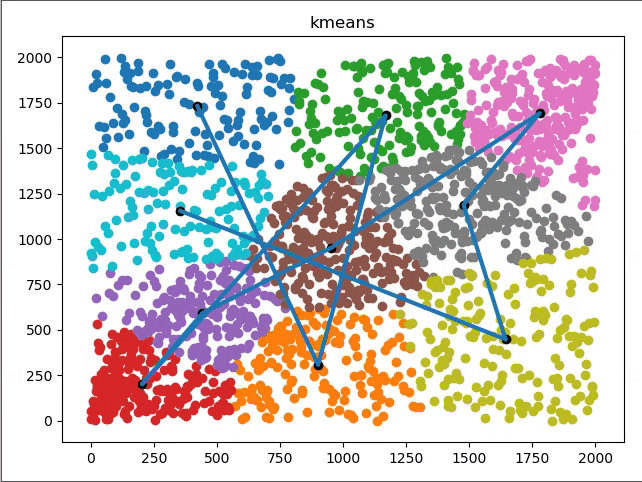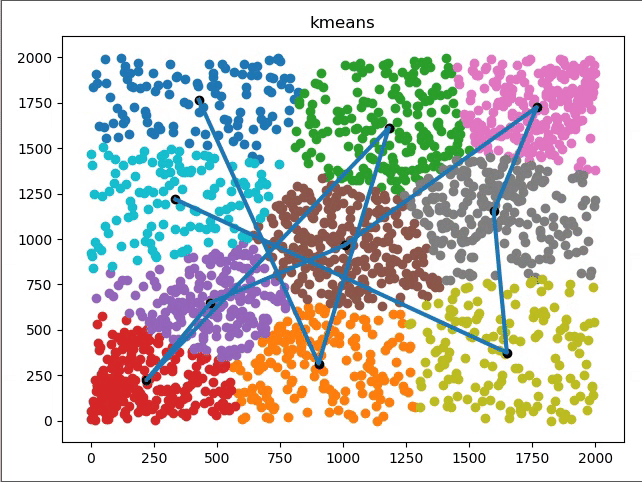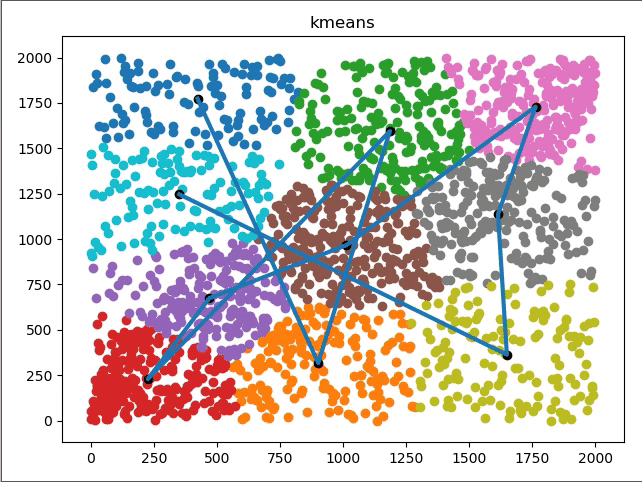
看看具体聚类过程图形化表示:

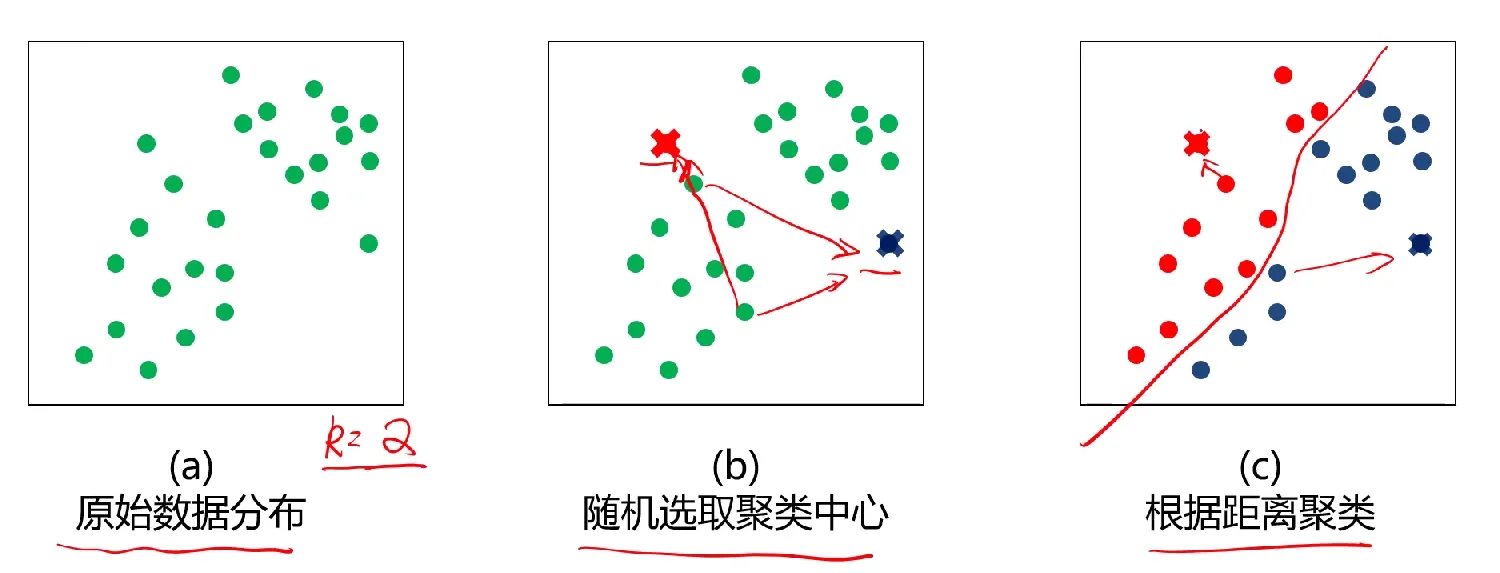
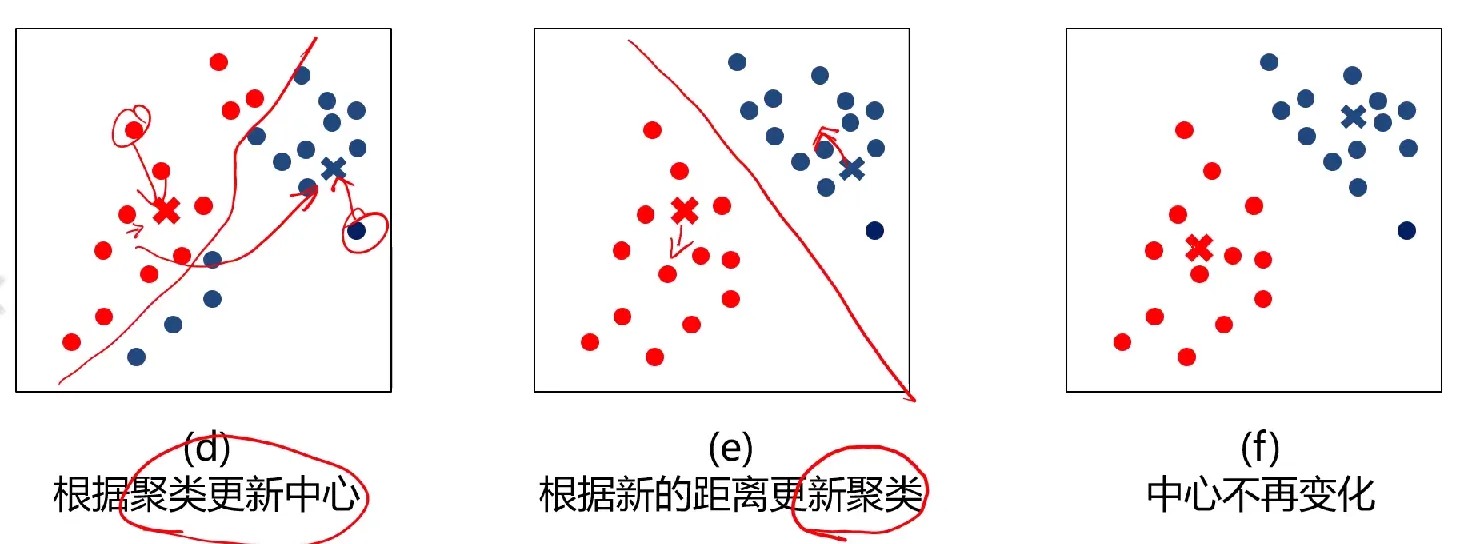
K-Means VS KNN

这里顺便说下KNN算法与K-Means的不同：

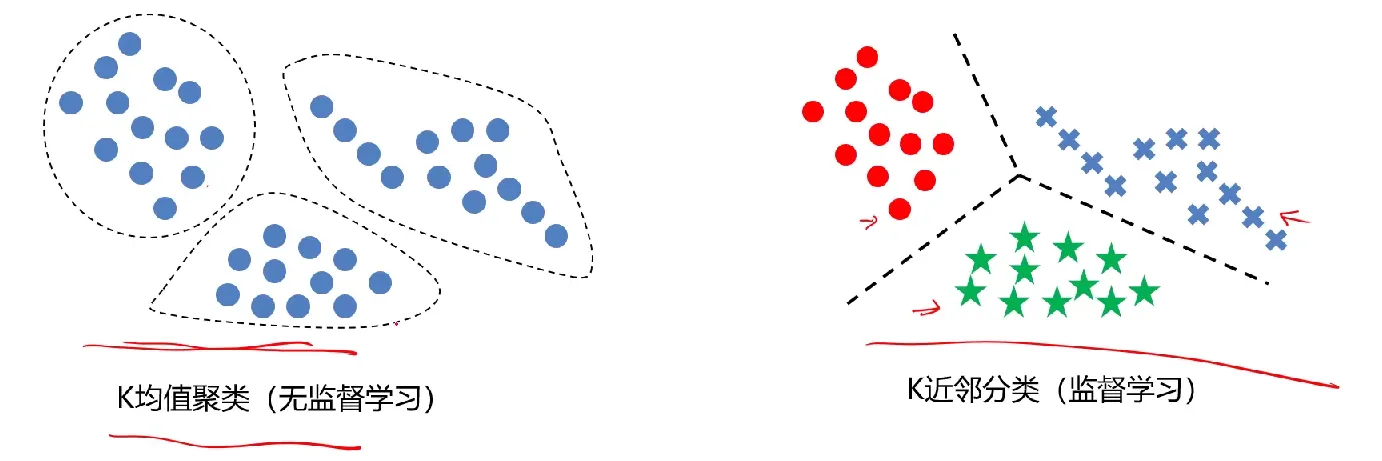KNN是给定一个训练数据集，对新的输入实例，在训练数据集中找到与该实例最邻近的K个实例(也就是上面所说的K个邻居）这K个实例的多数属于某个类，则把该输入实例分类到这个类中。应该算得上是最简单的机器学习算法之一了。

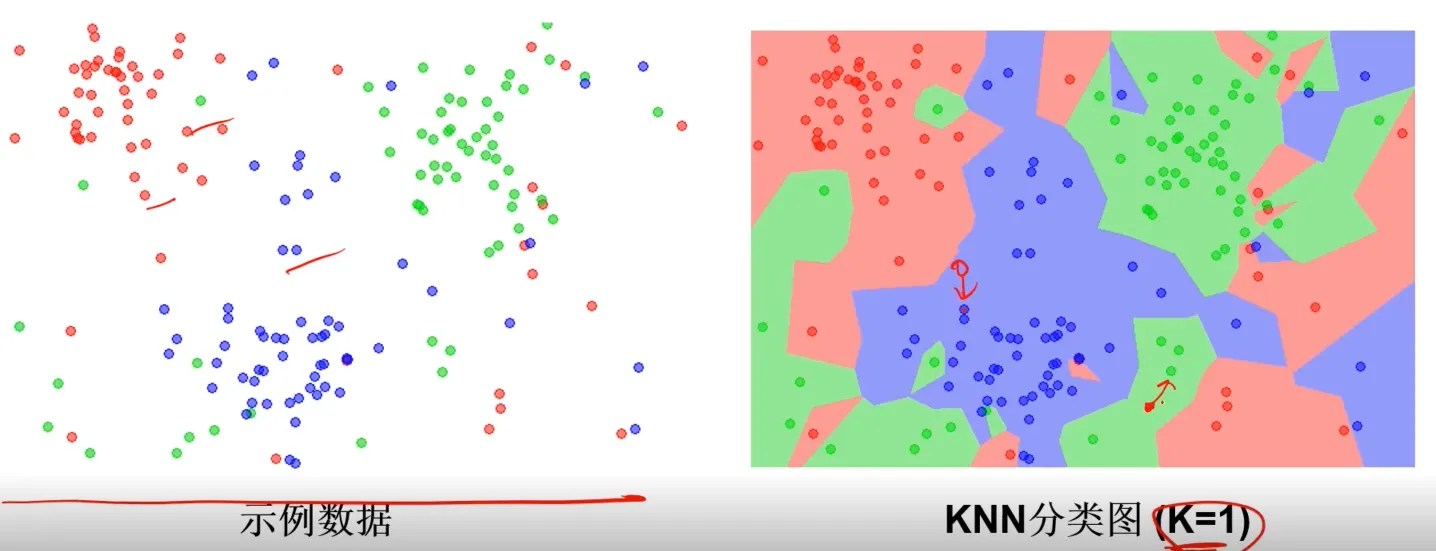
举例：K=3，绿色圆点的最近的3个邻居是2个红色小三角形和1个蓝色小正方形，判定绿色的待分类点属于红色的三角形一类；如果K=5，绿色圆点的最近的5个邻居是2个红色三角形和3个蓝色的正方形，判定绿色的待分类点属于蓝色的正方形一类。

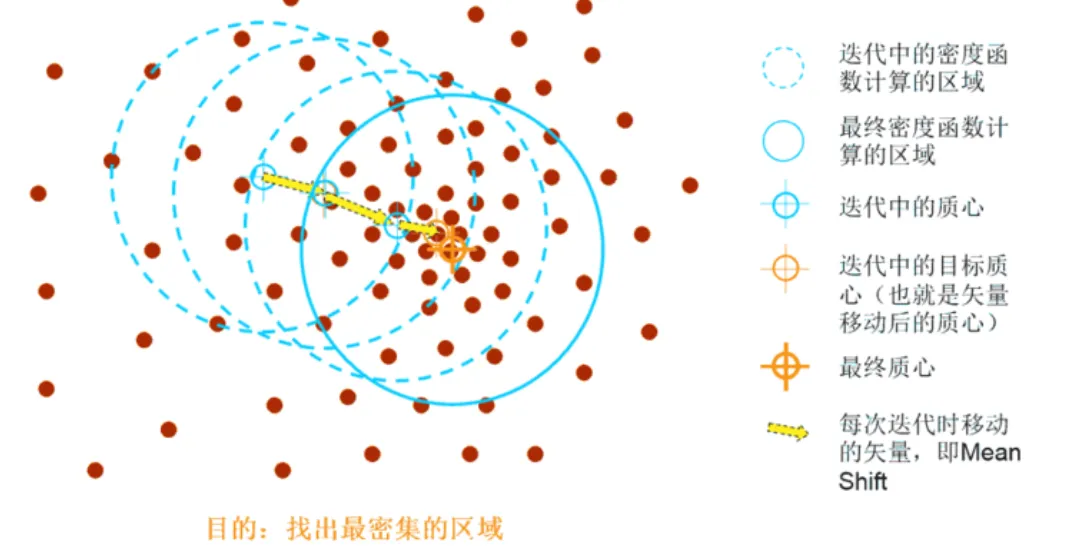
2、Mesn-shift 均值漂移聚类

均值漂移算法:一种基于密度梯度上升的聚类算法(沿着密度上升方向寻找聚类中心点)

Mesn-shift公式定义

均值漂移：$M(x)=\begin{aligned}\frac{1}{k}\sum_{x_i\in s_h}(u-x_i)\end{aligned}$\

中心点更新： $u^{t+1}=M^t+u^t$ 其中，$s_h$ 是以u为中心点，半径为 h 的高位球区域；k 是指包含在 $s_h$ 范围内点的个数；$x_i$ 是指包含在包含在$s_h$ 范围内的点 $M^{t}$ 表示 t 状态求得的漂移均值，$u^t$ 为t状态下的中心。

Mesn-shift算法流程

1、随机选择未分类点作为中心点

2、找出离中心点距离在带宽之内的点，记做集合S

3、计算从中心点到集合S中每个元素的偏移向量M

4、中心点以向量M移动

5、重复步骤2-4，直到收敛

6、重复1-5直到所有的点都被归类

7、取访问频率最大的那个类，作为当前点集的所属类

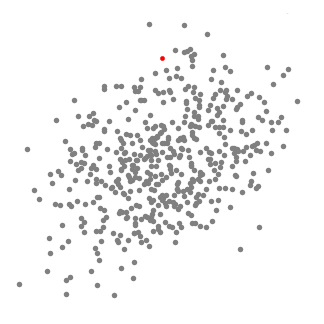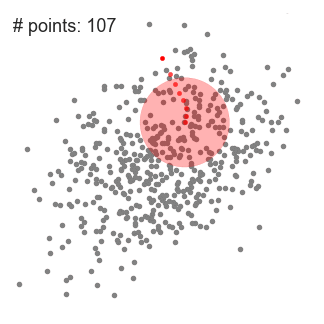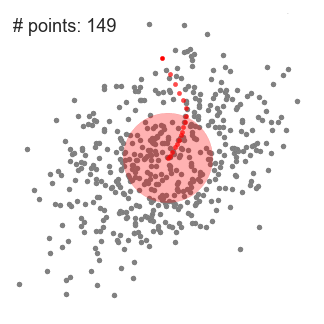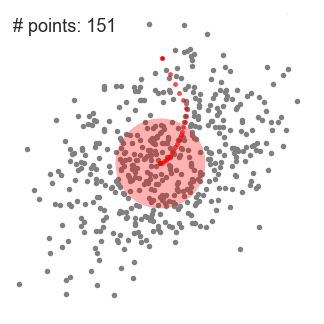
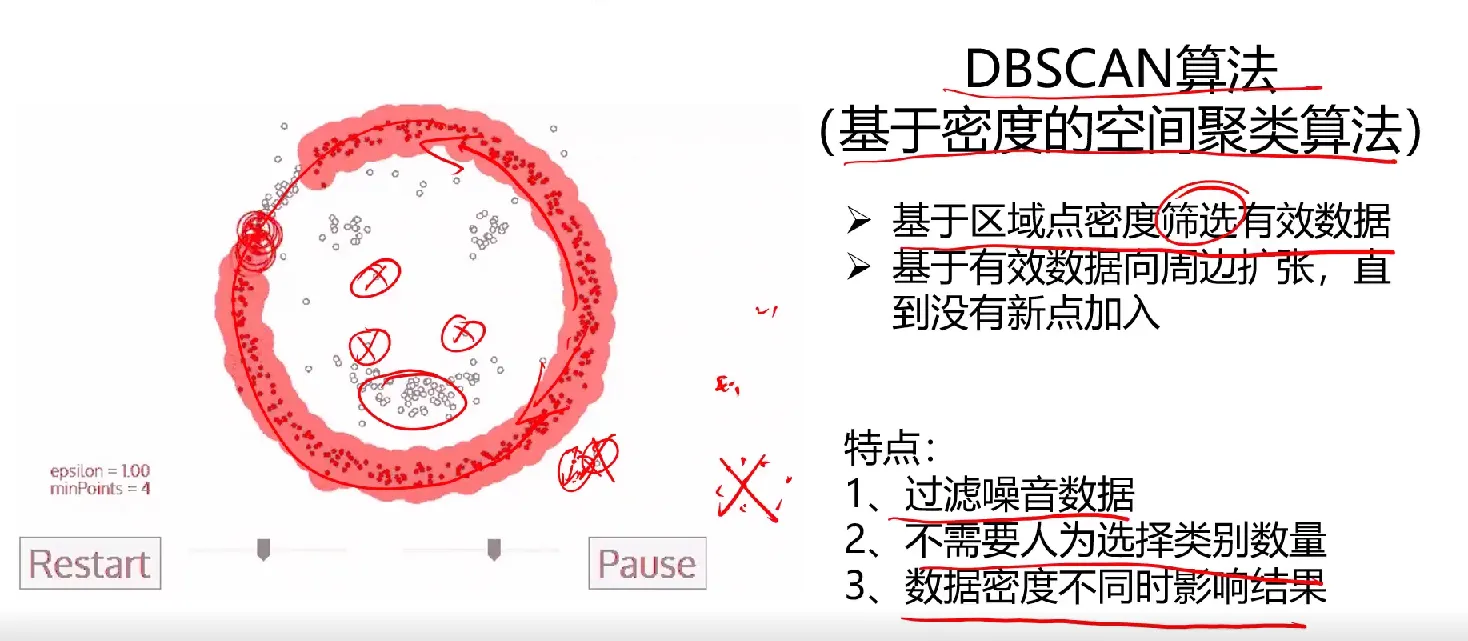
3、DBSCAN算法

思考题

问题：KMeans、KNN、Mean-shift算法分别有什么特点，在数据划分任务中，他们分别是如何执行的?

他们算法之间的根本区别是，K-means、Mean-shift本质上是无监督学习，而KNN是监督学习；K-means是聚类算法，KNN是分类（或回归）算法。

从直观感觉上，K-means比较吃经验，不管是类别数目的确定，还是初始中心点的确定都会影响聚类的结果，Mean-shift也是同理，数据半径的选择很重要。K-means与Mean-shift核心区别就是一个依靠欧式距离寻找中心点，一个依靠给定范围通过密度计算得到中心点。

三种算法都包含给定一个点，在数据集中查找离它最近的点的过程。只不过对于无监督学习的K-means、Mean-shift算法，需要不断迭代找到最优中心点，而KNN是给定了中心点直接硬算看谁占比大就归谁。