对垃圾邮件进行检测分类是机器学习中的经典案例，如何对垃圾邮件进行检测呢？首先需要人为标注样本邮件为垃圾/正常，然后计算机获取匹配的样本邮件及其标签，学习其特征，后面计算机针对新的邮件，自动识别其类型。用于帮助判断是否为垃圾邮件的属性，比如正文包含：现金、领取、红包、优惠、新品推广、季末促销、优惠套餐、折扣优惠、积分优惠等等。对于分类问题还比如图像分类、数字识别、考试通过预测……

常见分类方法

下面是一些常见的分类方法：

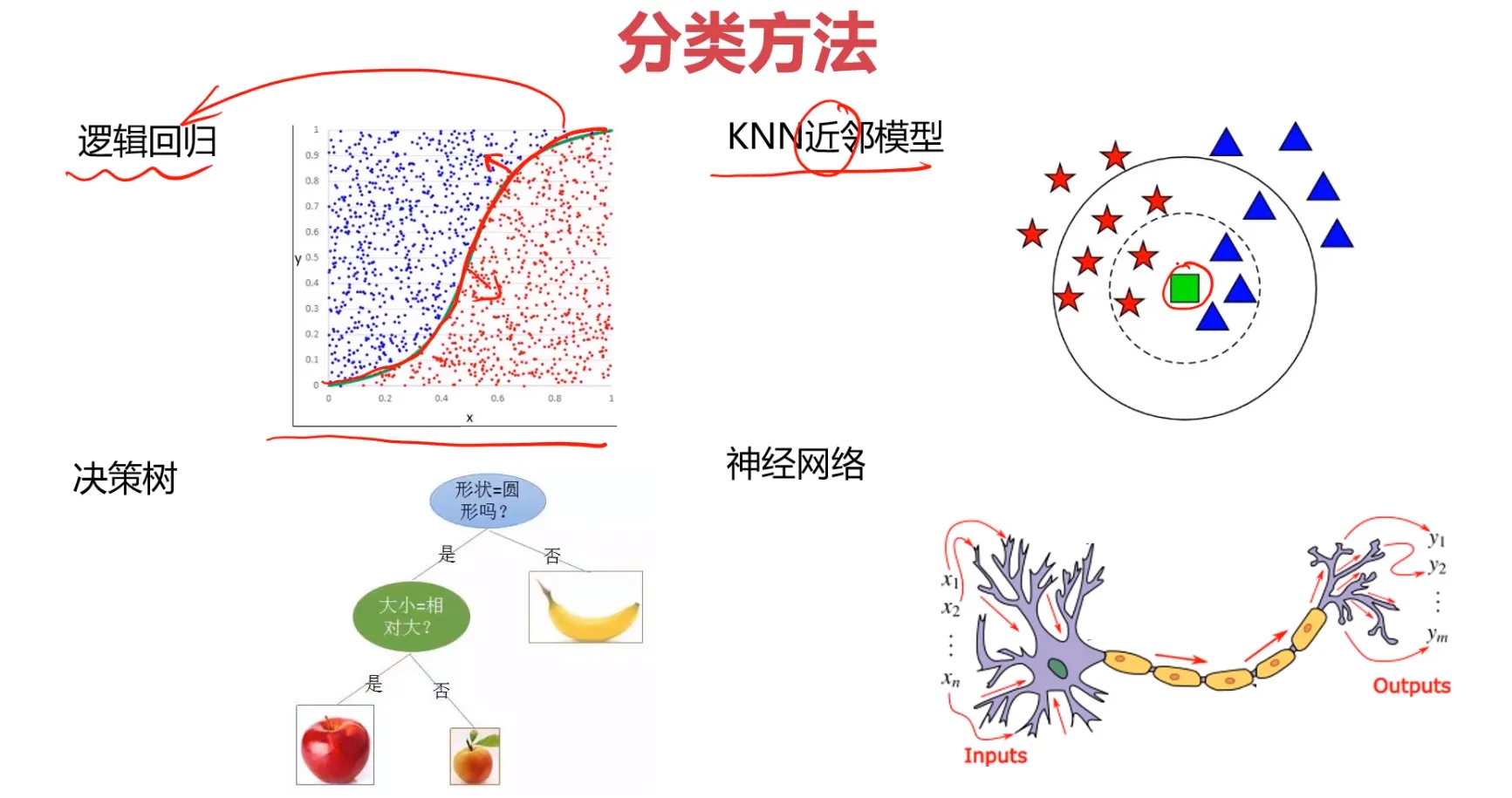
1、逻辑回归虽然被称为回归，但其实际上是分类模型，并常用于二分类。逻辑回归的本质是：假设数据服从这个分布，然后使用极大似然估计做参数的估计。其实就是一个被逻辑方程归一化后的线性回归，仅此而已。

2、KNN是通过测量不同特征值之间的距离进行分类。思路是：如果一个样本在特征空间中的k个最邻近的样本中的大多数属于某一个类别，则该样本也划分为这个类别。

3、决策树也是一种基本的分类方法，也可以用于回归。从形式上，决策树就是一棵按照各个特征建立的树形结构，叶节点表示对于的类别，特征选择的顺序不同，得到的树的形状也不同。

4、神经网络，是一种应用类似于大脑神经突触联接的结构，进行信息处理的数学模型。在这种模型中，大量的节点或称神经元之间相互联接构成网络，即神经网络，以达到处理信息的目的。

分类任务与回归任务的区别

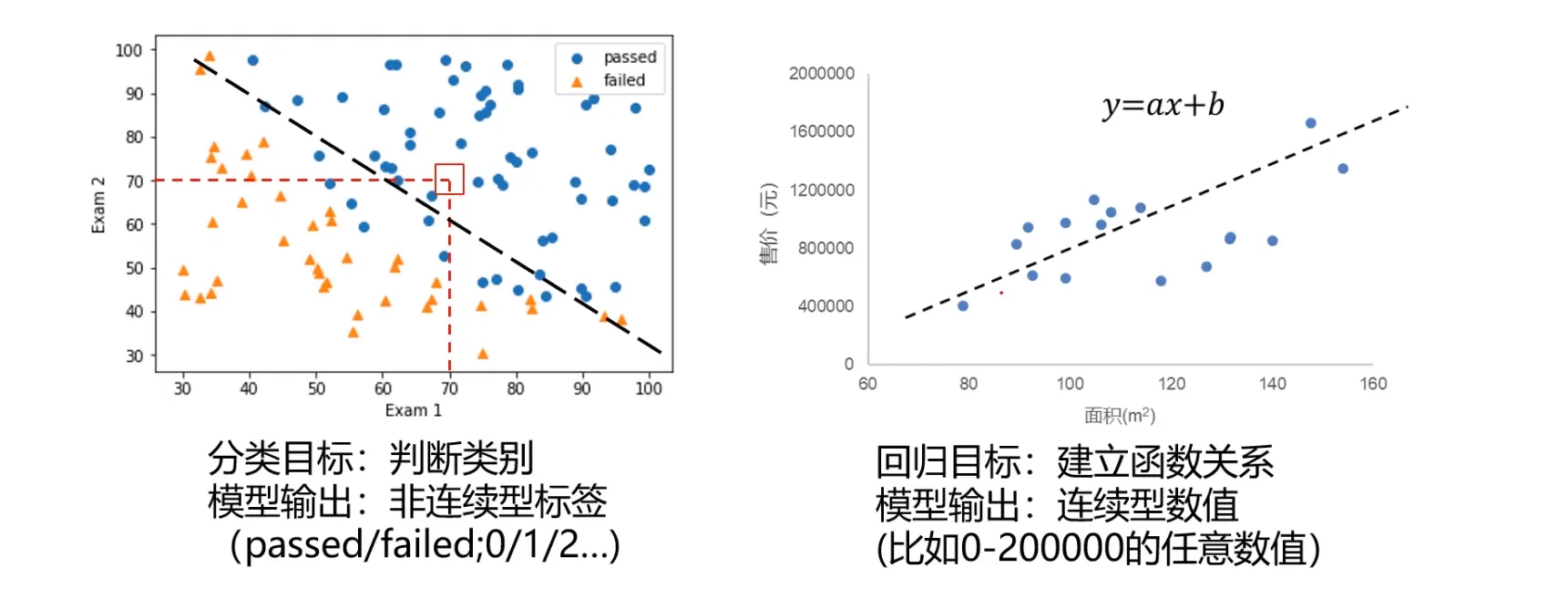
逻辑回归示例

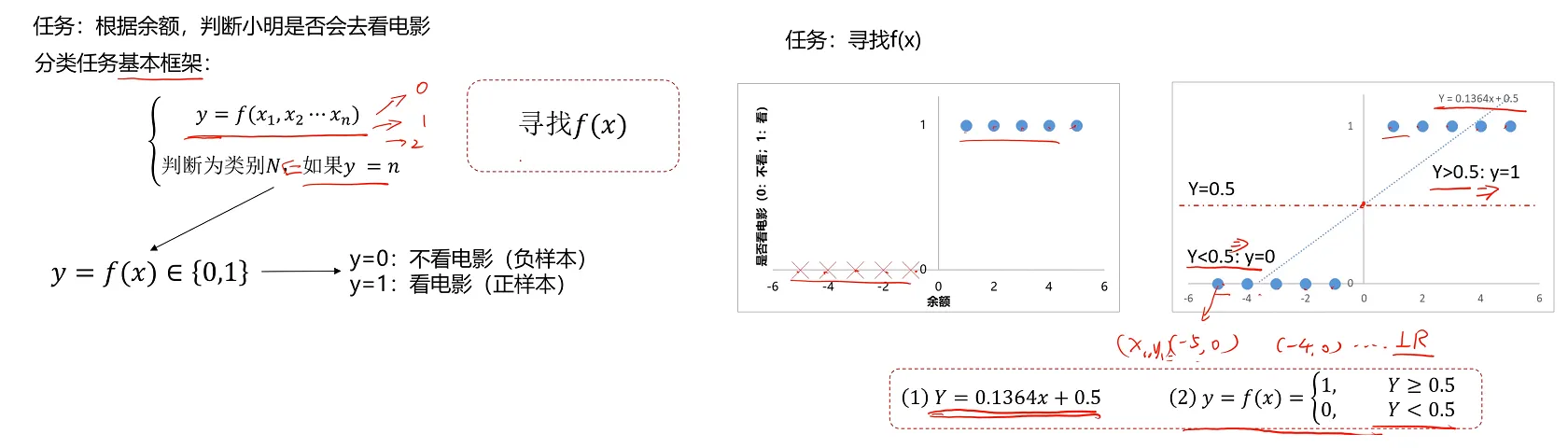
以是否看电影为例（如果运用线性回归模型）

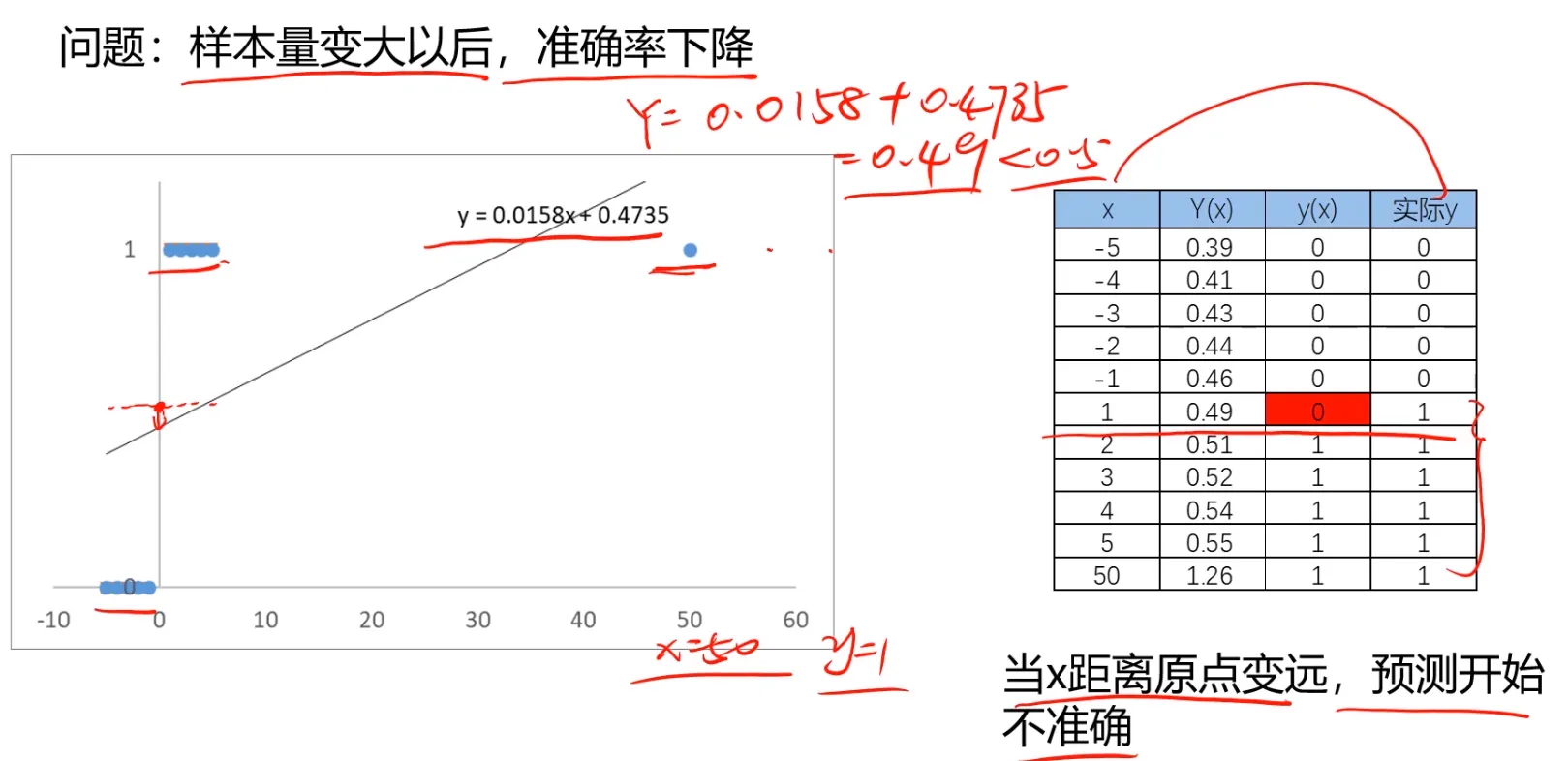
但是呢，如果运用线性回归模型，是存在局限性的：样本量变大之后，准确率会下降，即离散的点会导致回归曲线偏离： 如果由线性回归模型换成逻辑回归模型：

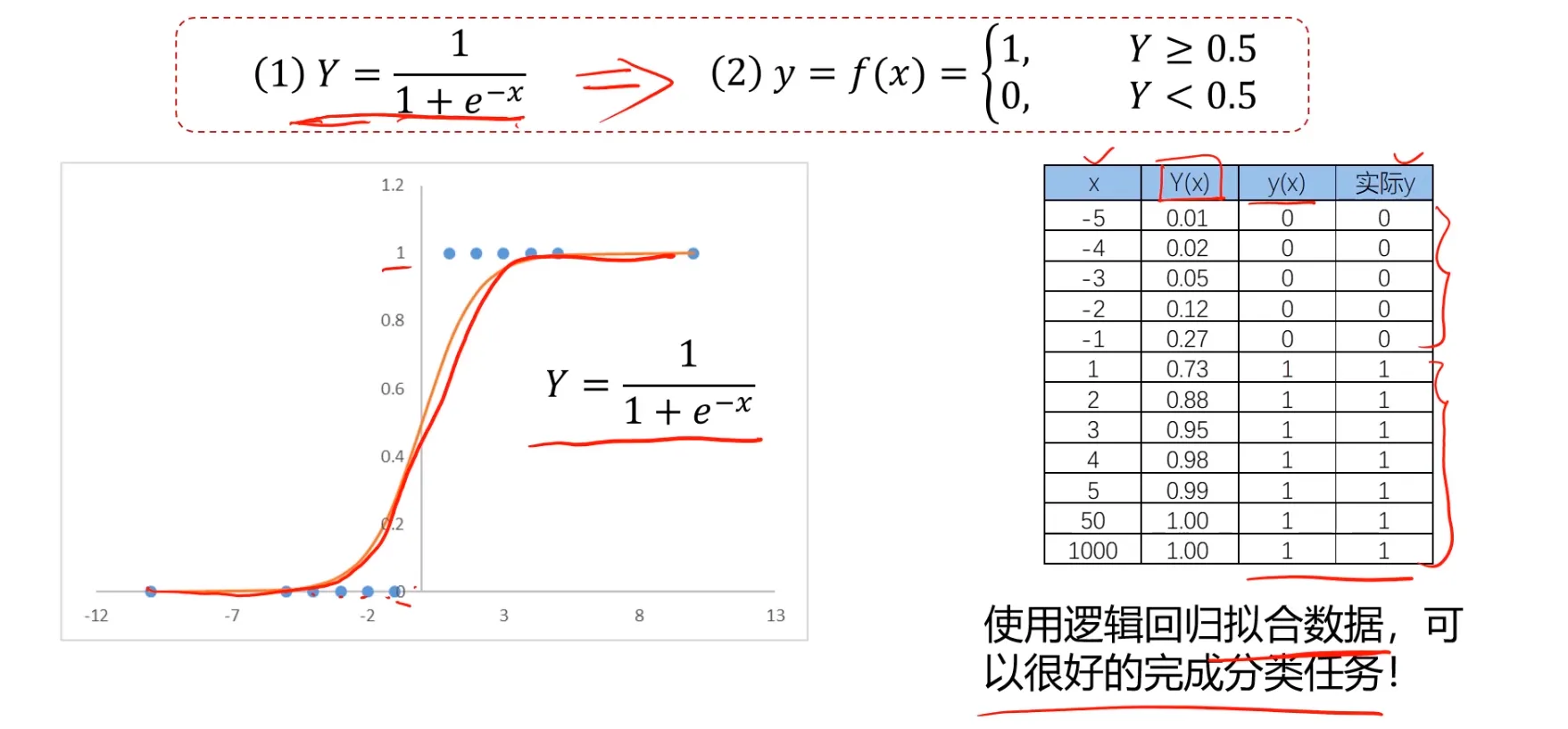逻辑回归是一种用于解决分类问题的模型，根据数据特征或属性，计算其归属于某一类别的概率P(x)，根据概率数值判断其所属类别。主要应用场景：二分类问题

数学表达式（sigmoid方程）： $$ \begin{gathered} P(x)=\frac{1}{1+e^{-x}} \ y=\begin{cases}1,\quad&P(x)\geq0.5\ 0,\quad&P(x)<0.5\end{cases} \end{gathered} $$

其中 y 为类别结果，P为概率分布函数，x为特征值。

当有两个x时，分类任务变得更为复杂，（线性）三角形和圆形是类别结果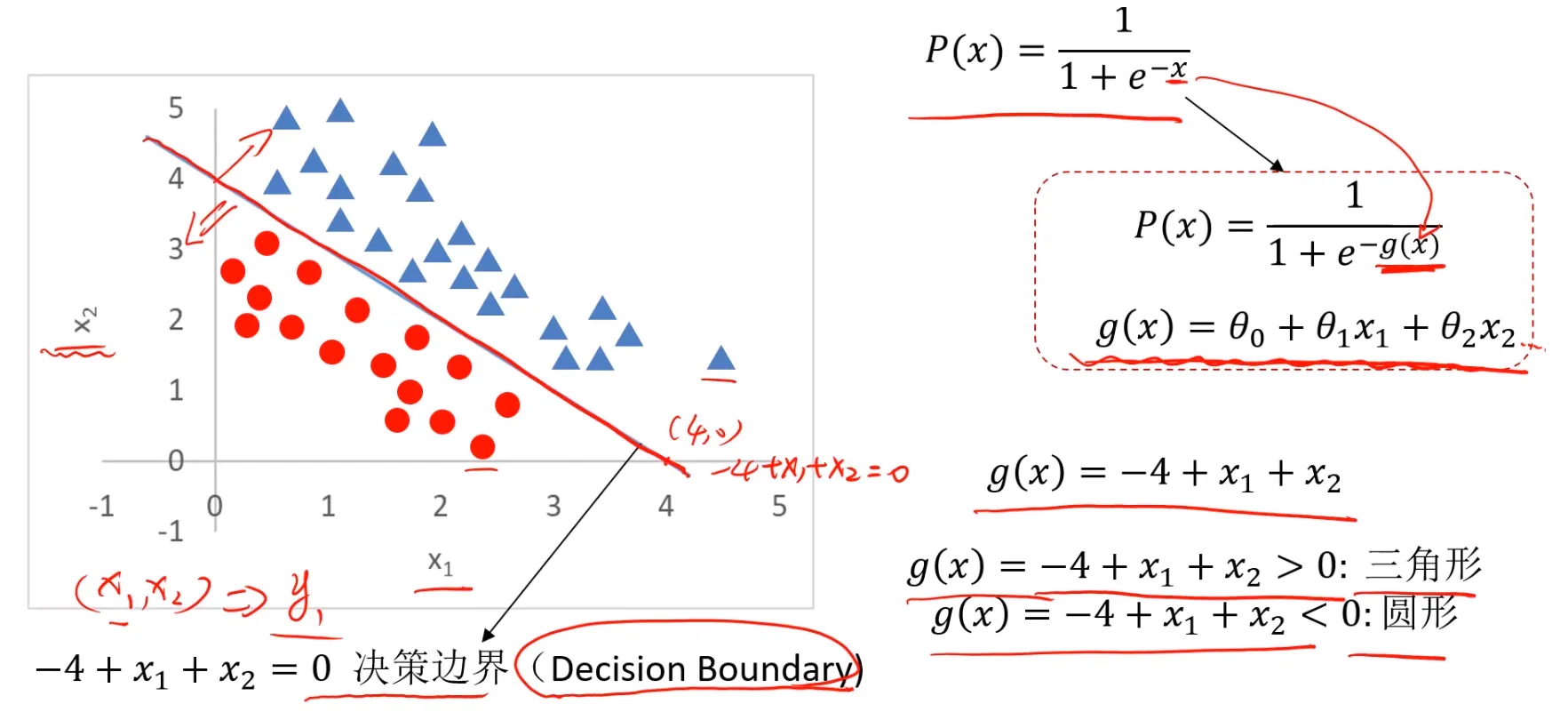： 非线性情况：

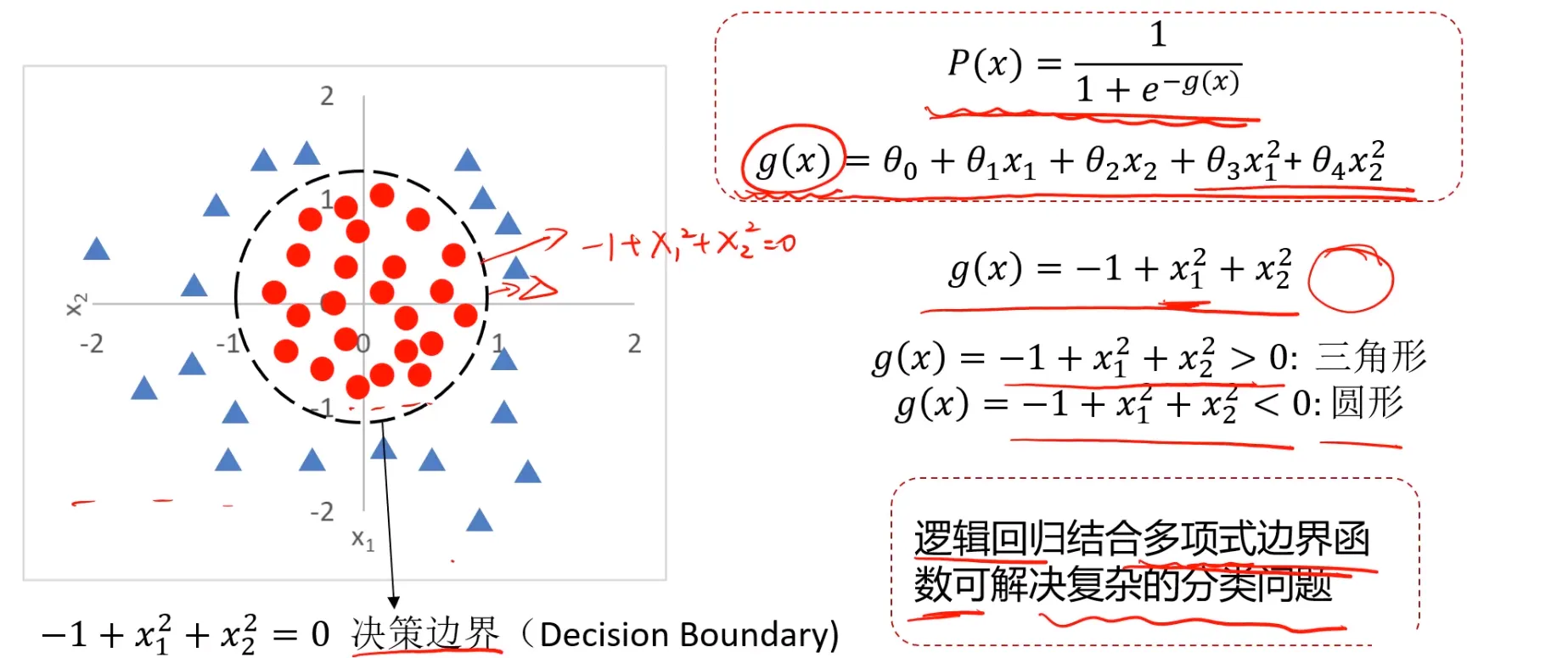
逻辑回归问题求解

$$ \begin{aligned} &P(x)=\frac{1}{1+e^{-g(x)}} \ & \ &g(x)=\theta_0+\theta_1x_1+\cdots \end{aligned} $$ 逻辑回归求解则是根据训练样本，寻找类别边界以及 $θ_0,θ_1,θ_2$ 可以回顾下线性回归中的求解方式，那就是可以使用损失函数，我们期望损失函数最小化：

$$ J=\frac{1}{2m}\sum_{i=1}^m(y_i'-y_i)^2 $$

但是在分类问题中，标签与预测结果都是离散点（0和1），使用该损失函数无法寻找极小值点 即我们在预测当中，当 $y=0$ 时，希望预测结果 $y'→0$ ;如果预测出来 $y'→1$，那么J会非常大，以此来惩罚，所以也是一种损失函数，通过J的大小变化告诉计算机预测是否准确：

$$ \begin{gathered} J_i=\begin{cases}-\log\left(P(x_i)\right),ify_i=1\ -\log\left(1-P(x_i)\right),{ify_i=0}\end{cases} \ & \ J=\frac{1}{m}\sum_{i=1}^{m}J_i=-\frac{1}{m}\left[\sum_{i=1}^{m}\big(y_i\log\big(P(x_i)\big)+(1-y_i)\log\big(1-P(x_i)\big)\big)\right] \end{gathered} $$

损失函数画出来大概就是如下所示：

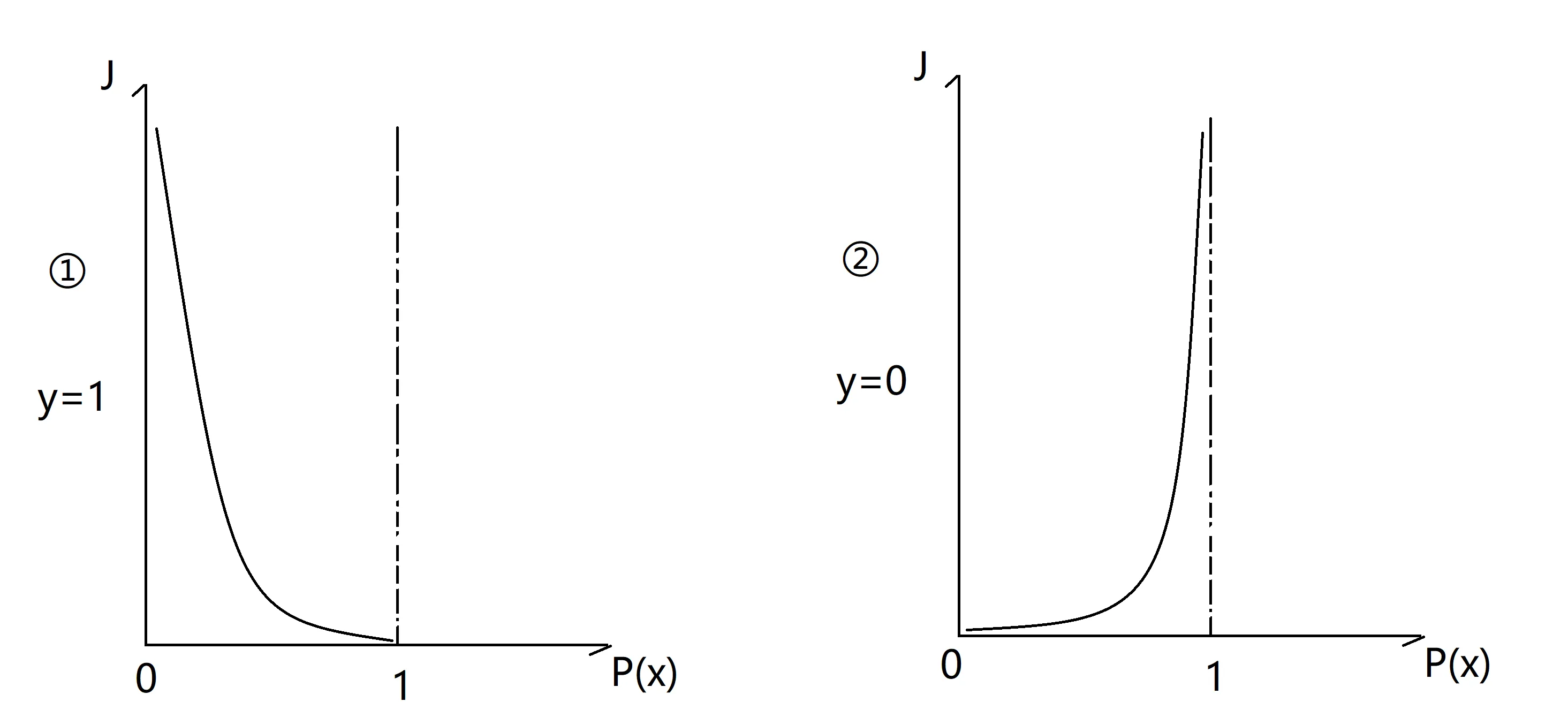
• $y=0$ 即当一个样本为负样本时，若 $P_x$ 的结果接近1（即预测为正样本），那么 $-\log(1-h_{\theta}(x))$ 的值很大，那么得到的惩罚就大。

• $y=1$ 当一个样本为正样本时，若 $P_x$ 的结果接近0（即预测为负样本），那么 $-\log(h_{\theta}(x))$ 的值很大，那么得到的惩罚就大。