多因子线性回归

发表于： 2023-06-11 分类于：机器学习与AI

字数： 511 阅读：≈ 3分钟

什么是回归分析？(Regression Analysis) 回归分析是一种统计方法，用于显示两个或更多变量之间的关系。该方法检验因变量与自变量之间的关系，常用图形表示。通常情况下，自变量随因变量而变化，并且通过回归分析确定出哪些因素对该变化最重要。

回归问题

函数表达式： $$ y=f(x_1,x_2\cdots x_n) $$

其实，回归问题可以如下分类：

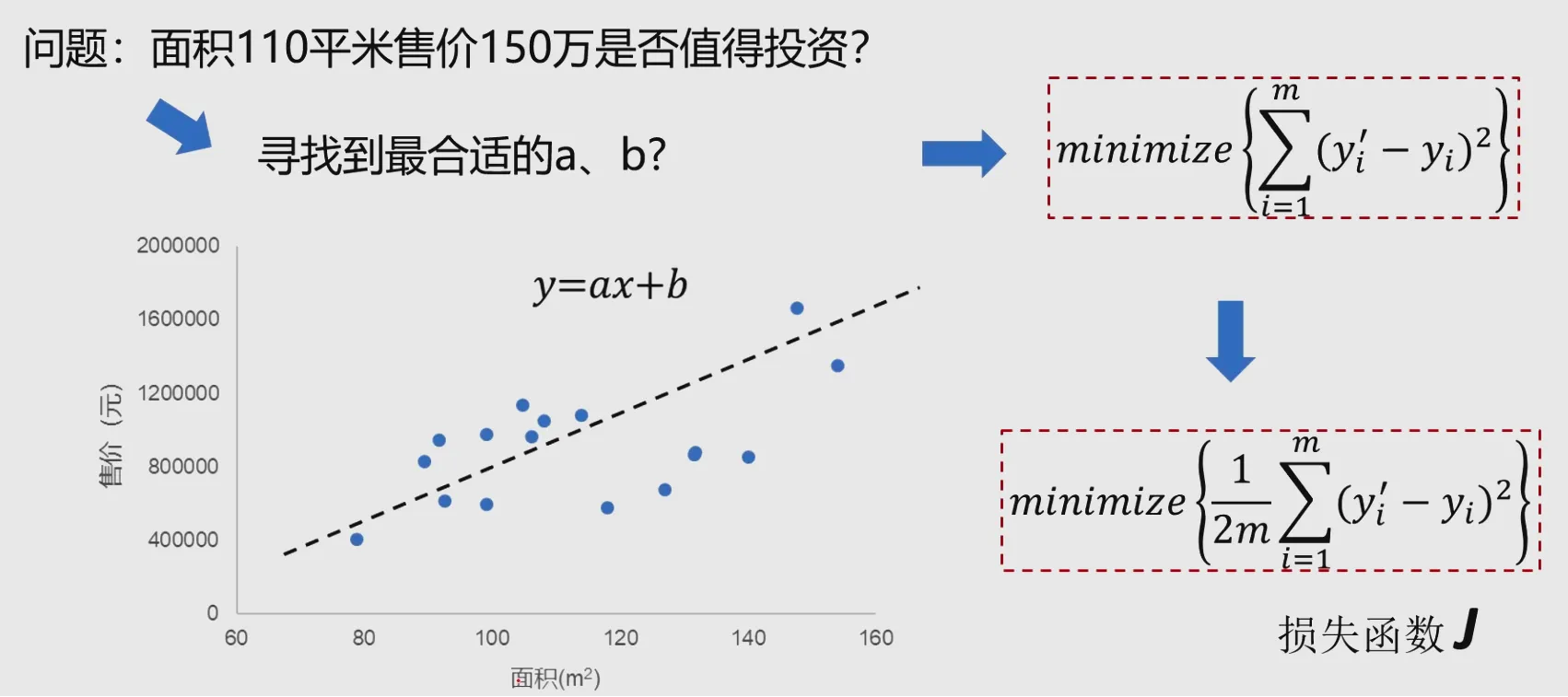
之所以称之为线性回归是因为变量与因变量之前是线性关系，比如 $$ y = ax+b $$

对于一组数据集，我们希望找到上面这个函数，这个函数会尽可能的拟合数据集，我们希望这个函数在X上每一个取值的函数值$X_i$与Y上每一个对应的$y_i$的平方差尽可能小。则平方损失函数如下： $$ loss(w,b)=\frac{1}{N}\sum_{i=0}^N(wx_i+b-y_i)^2 $$

梯度下降法：寻找极小值的一种方法。通过向函数上当前点对应梯度（或者是近似梯度）的反方向的规定步长距离点进行迭代搜索，直到在极小点收敛。 $$ J = f(p) $$ 具体求解方法： $$ p_{i+1}=p_i-\alpha\frac{\partial}{\partial p_i}f(p_i) $$

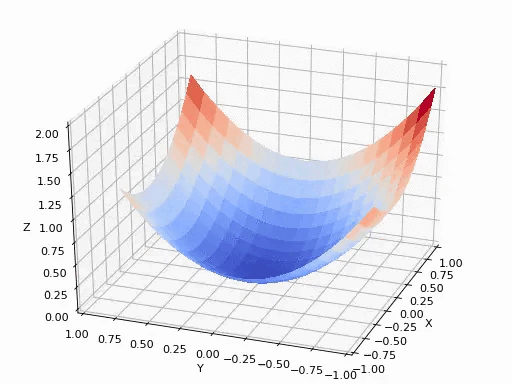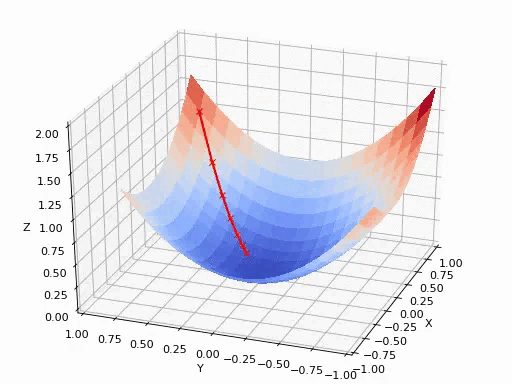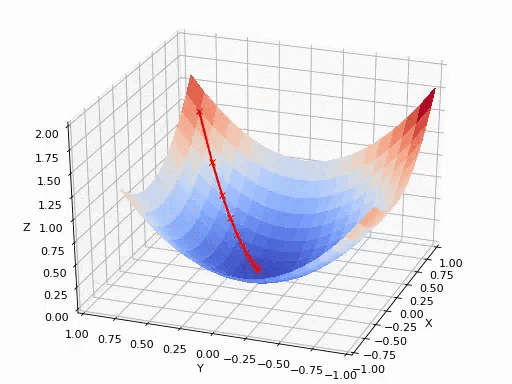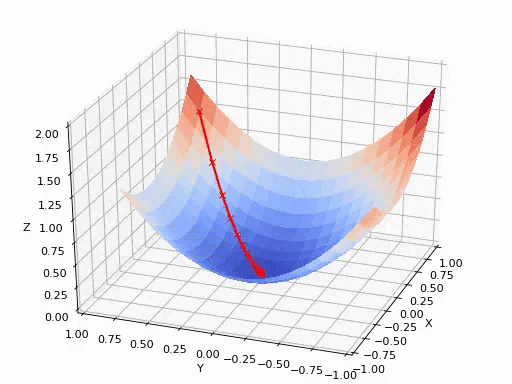
可以参考后面的《如何通俗理解梯度下降法》，在此不再赘述。

一元线性回归实战

基于usa_housing_price.csv数据，建立线性回归模型，预测合理房价:

1、以面积为输入变量，建立单因子模型，评估模型表现，可视化线性回归预测结果

2、以income、house age、numbers of rooms、population、area为输入变量，建立多因子模型，评估模型表现

3、预测Income=65000，House Age=5，Number of Rooms=5，Population=30000,size=200的合理房价

import pandas as pd
import numpy as np
data = pd.read_csv('usa_housing_price.csv')
data.head()
# print(type(data), data.shape)

数据如下：

	Avg. Area Income	Avg. Area House Age	Avg. Area Number of Rooms	Area Population	size
0	79545.45857	5.317139	7.009188	23086.80050	188.214212
1	79248.64245	4.997100	6.730821	40173.07217	160.042526
2	61287.06718	5.134110	8.512727	36882.15940	227.273545
3	63345.24005	3.811764	5.586729	34310.24283	164.816630
4	59982.19723	5.959445	7.839388	26354.10947	161.966659
...	...	...	...	...	...
4995	60567.94414	3.169638	6.137356	22837.36103	161.641403
4996	78491.27543	4.000865	6.576763	25616.11549	159.164596
4997	63390.68689	3.749409	4.805081	33266.14549	139.491785
4998	68001.33124	5.465612	7.130144	42625.62016	184.845371
4999	65510.58180	5.007695	6.792336	46501.28380	148.589423

5000 rows × 5 columns

# visualize data
# 先以面积作为输入变量
from matplotlib import pyplot as plt
fig = plt.figure(figsize=(10,10))

# 子图位置限定
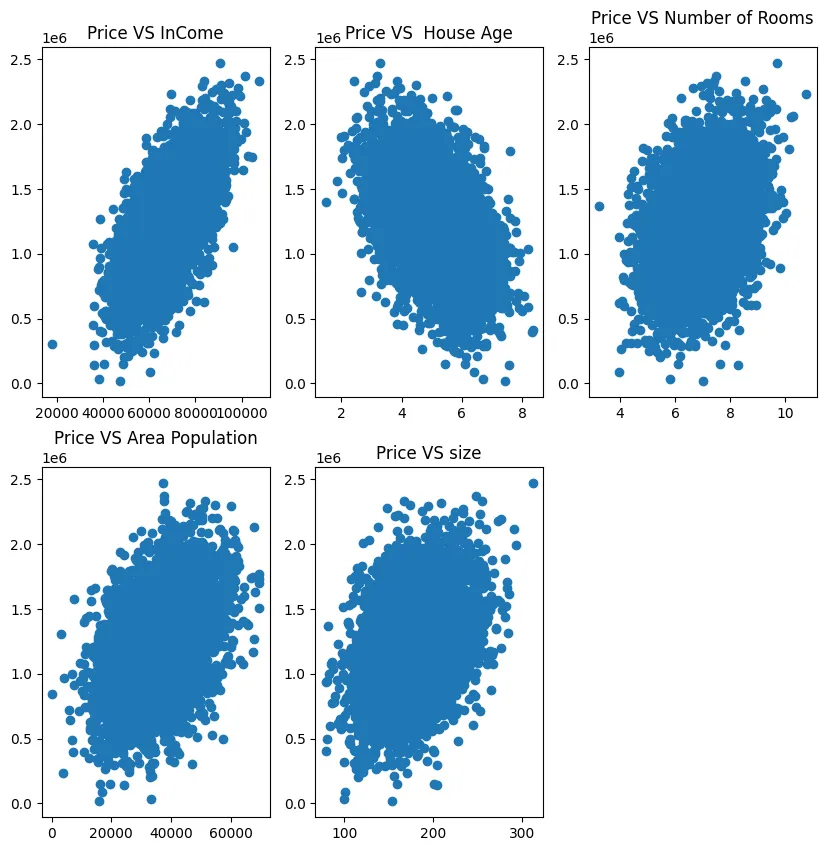
fig1 = plt.subplot(231)
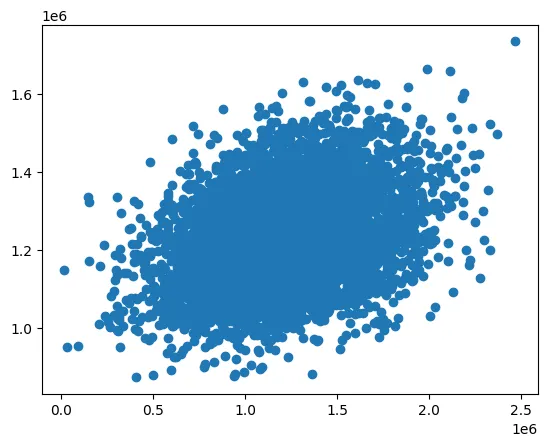
plt.scatter(data.loc[:, 'Avg. Area Income'], data.loc[:, 'Price'])
plt.title('Price VS InCome')

fig2 = plt.subplot(232)
plt.scatter(data.loc[:, 'Avg. Area House Age'], data.loc[:, 'Price'])
plt.title('Price VS  House Age')

fig3 = plt.subplot(233)
plt.scatter(data.loc[:, 'Avg. Area Number of Rooms'], data.loc[:, 'Price'])
plt.title('Price VS Number of Rooms')

fig3 = plt.subplot(234)
plt.scatter(data.loc[:, 'Area Population'], data.loc[:, 'Price'])
plt.title('Price VS Area Population')

fig3 = plt.subplot(235)
plt.scatter(data.loc[:, 'size'], data.loc[:, 'Price'])
plt.title('Price VS size')

plt.show()

# define x and y
X = data.loc[:, 'size']
y = data.loc[:, 'Price']
# X.head()
y.head()

0    1.059034e+06
1    1.505891e+06
2    1.058988e+06
3    1.260617e+06
4    6.309435e+05
Name: Price, dtype: float64

X = np.array(X).reshape(-1,1)
print(X.shape)

(5000, 1)

# set up the linear regression model
from sklearn.linear_model import LinearRegression

LR1 = LinearRegression()

# 训练模型 train model
LR1.fit(X,y)

LinearRegression()

# 单因子预测 calc size vs price
y_predict1 = LR1.predict(X)
print(y_predict1)

[1276881.85636623 1173363.58767144 1420407.32457443 ... 1097848.86467426
 1264502.88144558 1131278.58816273]

from sklearn.metrics import mean_squared_error, r2_score

MSE_1 = mean_squared_error(y, y_predict1)
R2_1 = r2_score(y, y_predict1)
print(MSE_1, R2_1)

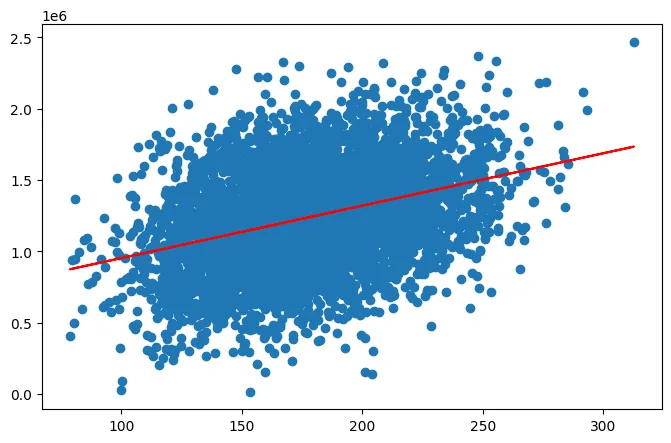
通过预测出来的 y_predict 的值来评估线性回归模型的表现，其中主要是通过 MSE 以及 R2_1 来作为判别的标准( MSE 的值越小越好，R2_1 的值越接近1越好)：

108771672553.62639 0.1275031240418235

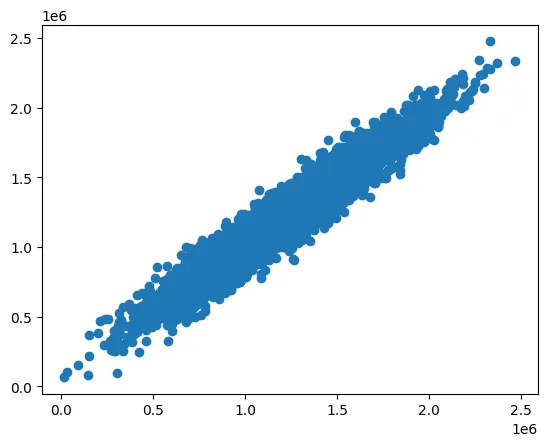
plt.figure(figsize=(8,5))
plt.scatter(X, y)
plt.plot(X,y_predict1, 'r')
plt.show()

多因子回归

以income、house age、numbers of rooms、population、area为输入变量，建立多因子模型，评估模型表现

#define X_multi
X_multi = data.drop(['Price'], axis=1)
X_multi

	Avg. Area Income	Avg. Area House Age	Avg. Area Number of Rooms	Area Population	size
0	79545.45857	5.317139	7.009188	23086.80050	188.214212
1	79248.64245	4.997100	6.730821	40173.07217	160.042526
2	61287.06718	5.134110	8.512727	36882.15940	227.273545
3	63345.24005	3.811764	5.586729	34310.24283	164.816630
4	59982.19723	5.959445	7.839388	26354.10947	161.966659
...	...	...	...	...	...
4995	60567.94414	3.169638	6.137356	22837.36103	161.641403
4996	78491.27543	4.000865	6.576763	25616.11549	159.164596
4997	63390.68689	3.749409	4.805081	33266.14549	139.491785
4998	68001.33124	5.465612	7.130144	42625.62016	184.845371
4999	65510.58180	5.007695	6.792336	46501.28380	148.589423

5000 rows × 5 columns

Tim's Note

多因子线性回归

回归问题

一元线性回归实战

多因子回归

Reference