索引堆的实现与优化
在之前文章中记述了堆的实现(插入方式建堆、heapify方式建堆以及堆排序) 《 堆的实现及其应用 》 。今天来看看索引堆是个什么东西,对于我们所关心的这个数组而言,数组中的元素位置发生了改变。正是因为这些元素的位置发生了改变,我们才能将其构建为最大堆。 如果元素十分复杂的话,比如像每个位置上存的是一篇上万字的文章。那么交换它们之间的位置将产生大量的时间消耗。并且由于数组元素的位置在构建成堆之后发生了改变,那么我们就很难索引到它,很难去改变它。可以在每一个元素上再加上一个属性来表示原来的位置可以解决,但是这样的话,必须将这个数组遍历一下才能解决。针对以上问题,我们就需要引入索引堆(Index Heap)的概念。
索引堆基本实现
对于索引堆来说,我们将数据和索引这两部分分开存储。真正表征堆的这个数组是由索引这个数组构建成的。
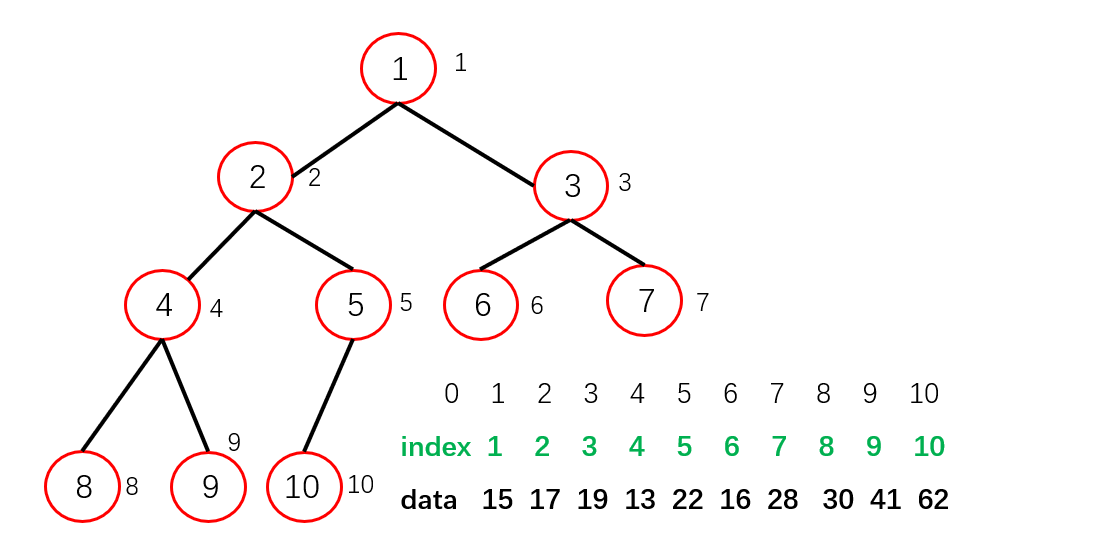
而在构建堆(以最大索引堆为例)的时候,比较的是data中的值(即原来数组中对应索引所存的值),构建成堆的却是index域。而构建完之后,data域并没有发生改变,位置改变的是index域。
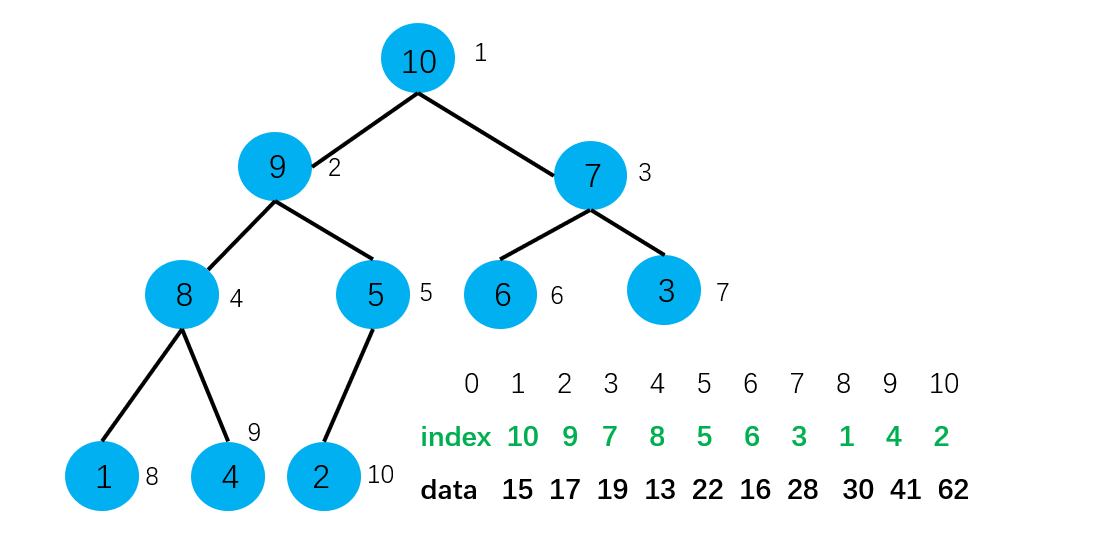
那么现在这个最大堆该怎么解读呢?例如,堆顶元素为Index=10代表的就是索引为10的data域的值,即62。这时我们来看,构建堆的过程就是简单地索引之间的交换,索引就是简单的int型。效率很高。
现在如果我们想对这个数组进行一些改变,比如我们想将索引为7的元素值改为100,那我们需要做的就是将索引7所对应data域的28改为100。时间复杂度为O(1)。当然改完之后,我们还需要进行一些操作来维持最大堆的性质。不过调整的过程改变的依旧是index域的内容。
package imooc.heap;
public class MaxIndexHeap {
protected int[] data;
protected int[] indexes;
//堆里有多少元素
protected int count;
//堆的容量
protected int capacity;
//因为0号位置不使用,所以capacity + 1
public MaxIndexHeap(int capacity) {
data = new int[capacity + 1];
indexes = new int[capacity + 1];
count = 0;
this.capacity = capacity;
}
public MaxIndexHeap(int[] arr){
data = new int[arr.length + 1];
capacity = arr.length + 1;
for (int i = 0; i < arr.length; i++) {
data[i + 1] = arr[i];
}
count = arr.length;
//从第一个不是叶子节点的位置开始
for (int i = count / 2; i >= 1; i--) {
shiftDown(i);
}
}
//获取现存元素个数
public int size(){
return count;
}
//判断是否为空
public boolean isEmpty(){
return count == 0;
}
//插入数据(传入的i对于用户而言,是从0开始索引的)
public void insert(int i, int item){
assert i + 1 >= 1;
i++; //i += 1
//判断容量知否超出
if(count + 1 >= capacity){
//开始扩容
resize();
}
//先存储到末尾
data[i] = item;
indexes[count + 1] = i;
count++;
//开始向上调堆
shiftUp(count);
}
//取出数据的索引
public int extractIndexMax(){
if(count == 0) throw new RuntimeException("Heap is null");
int ret = indexes[1] - 1;
swapIndexes(1, count);
count--;
//开始向下调堆
shiftDown(1);
return ret;
}
//根据索引获得元素
public int getItemByIndex(int index){
return data[index];
}
//根据索引修改某个元素
public void changeItem(int index, int newValue){
index++;
data[index] = newValue;
//找到indexes[j] = index; j表示data[index]在堆中的位置
//找到shiftUp(j),再shiftDown(j)
for (int j = 1; j <= count; j++) {
if(indexes[j] == index){
shiftUp(j);
shiftDown(j);
return;
}
}
}
//向下调堆
private void shiftDown(int k) {
while (2 * k <= count){
int j = 2 * k;
if(j + 1 <= count && data[indexes[j+1]] > data[indexes[j]]){
j++;
}
if(data[indexes[k]] >= data[indexes[j]]){
break;
}
swapIndexes(k, j);
k = j;
}
}
//向上调堆
private void shiftUp(int k) {
while(k > 1 && data[indexes[k / 2]] < data[indexes[k]]){
swapIndexes(k/2, k);
k /= 2;
}
}
//交换对应两个位置的值(这是其实是交换索引的位置)
private void swapIndexes(int i, int j){
int tmp = indexes[i];
indexes[i] = indexes[j];
indexes[j] = tmp;
}
//扩充容量
private void resize() {
int[] newData = new int[capacity * 2];
System.arraycopy(data, 0, newData, 0, count);
data = newData;
capacity *= 2;
int[] newIndexes = new int[capacity * 2];
System.arraycopy(indexes, 0, newIndexes, 0, count);
indexes = newIndexes;
}
}
索引堆的优化:反向查找
如何优化呢? 反向查找:再建立一个数组,这个数组的下标和原始数据数组的下标的意思是一样的,就是索引的意思。而数组中存储的元素则是索引在索引堆数组中的位置。
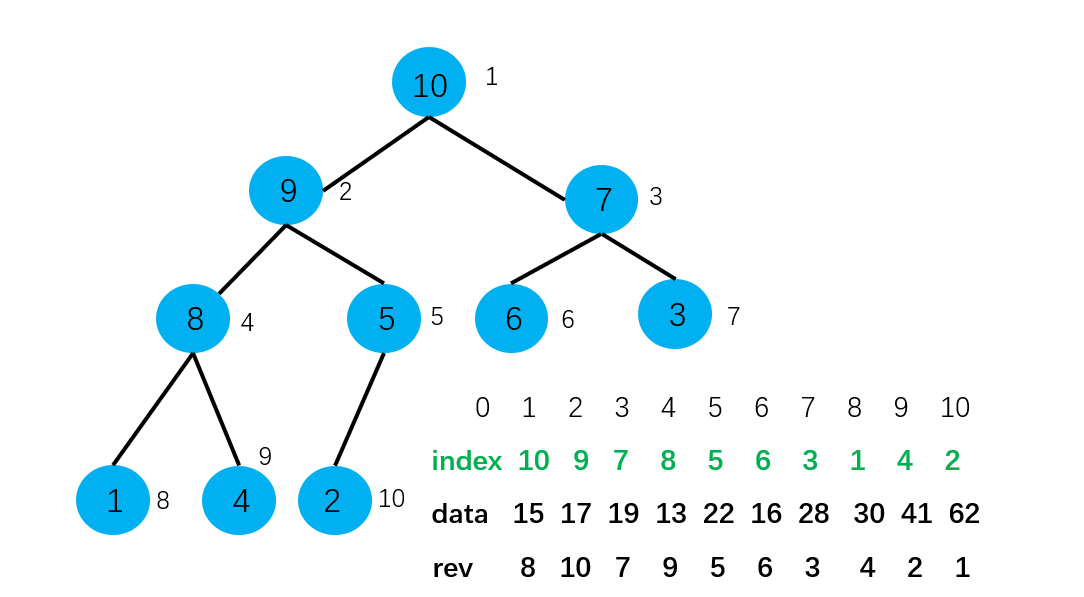
对反向查找表的维护就是,将索引堆中的值取出来(值就是索引值),这个值就是方向查找表的下标,那这个下标应该对应的元素就是索引堆中的位置。

public class MaxIndexHeapOptimize {
protected int[] data;
protected int[] indexes;
protected int[] reverse;
//堆里有多少元素
protected int count;
//堆的容量
protected int capacity;
//因为0号位置不使用,所以capacity + 1
public MaxIndexHeapOptimize(int capacity) {
data = new int[capacity + 1];
indexes = new int[capacity + 1];
reverse = new int[capacity + 1];
count = 0;
for (int i = 0; i <= capacity ; i++) {
reverse[i] = 0;
}
this.capacity = capacity;
}
public MaxIndexHeapOptimize(int[] arr){
data = new int[arr.length + 1];
capacity = arr.length + 1;
for (int i = 0; i < arr.length; i++) {
data[i + 1] = arr[i];
}
count = arr.length;
//从第一个不是叶子节点的位置开始
for (int i = count / 2; i >= 1; i--) {
shiftDown(i);
}
}
//获取现存元素个数
public int size(){
return count;
}
//判断是否为空
public boolean isEmpty(){
return count == 0;
}
//插入数据(传入的i对于用户而言,是从0开始索引的)
public void insert(int i, int item){
assert i + 1 >= 1;
i++; //i += 1
//判断容量知否超出
if(count + 1 >= capacity){
//开始扩容
resize();
}
//先存储到末尾
data[i] = item;
indexes[count + 1] = i;
reverse[i] = count + 1;
count++;
//开始向上调堆
shiftUp(count);
}
//取出数据的索引
public int extractIndexMax(){
if(count == 0) throw new RuntimeException("Heap is null");
int ret = indexes[1] - 1;
swapIndexes(1, count);
reverse[indexes[1]] = 1;
reverse[indexes[count]] = 0;
count--;
//开始向下调堆
shiftDown(1);
return ret;
}
//取出数据的索引
public int extractMax(){
if(count == 0) throw new RuntimeException("Heap is null");
int ret = data[indexes[1]];
swapIndexes(1, count);
reverse[indexes[1]] = 1;
reverse[indexes[count]] = 0;
count--;
//开始向下调堆
shiftDown(1);
return ret;
}
//根据索引获得元素
public int getItemByIndex(int index){
if(contain(index)){
throw new RuntimeException("This index is not in heap!");
}
return data[index];
}
//根据索引修改某个元素
public void changeItemOld(int index, int newValue){
index++;
data[index] = newValue;
//找到indexes[j] = index; j表示data[index]在堆中的位置
//找到shiftUp(j),再shiftDown(j)
for (int j = 1; j <= count; j++) {
if(indexes[j] == index){
shiftUp(j);
shiftDown(j);
return;
}
}
}
//根据索引修改某个元素
public void changeItem(int index, int newValue){
if(contain(index)){
throw new RuntimeException("This index is not in heap!");
}
index++;
data[index] = newValue;
//找到indexes[j] = index; j表示data[index]在堆中的位置
int j = reverse[index]; //O(1)的时间复杂度
shiftUp(j);
shiftDown(j);
}
private boolean contain(int index) {
if(!(index + 1 >= 0 && index + 1 <= capacity)){
throw new RuntimeException("This index is illegal");
}
return reverse[index + 1] == 0;
}
//向下调堆
private void shiftDown(int k) {
while (2 * k <= count){
int j = 2 * k;
if(j + 1 <= count && data[indexes[j+1]] > data[indexes[j]]){
j++;
}
if(data[indexes[k]] >= data[indexes[j]]){
break;
}
swapIndexes(k, j);
reverse[indexes[k]] = k;
reverse[indexes[j]] = j;
k = j;
}
}
//向上调堆
private void shiftUp(int k) {
while(k > 1 && data[indexes[k / 2]] < data[indexes[k]]){
swapIndexes(k/2, k);
reverse[indexes[k/2]] = k/2;
reverse[indexes[k]] = k;
k /= 2;
}
}
//交换对应两个位置的值(这是其实是交换索引的位置)
private void swapIndexes(int i, int j){
int tmp = indexes[i];
indexes[i] = indexes[j];
indexes[j] = tmp;
}
//扩充容量
private void resize() {
int[] newData = new int[capacity * 2];
System.arraycopy(data, 0, newData, 0, count);
data = newData;
capacity *= 2;
int[] newIndexes = new int[capacity * 2];
System.arraycopy(indexes, 0, newIndexes, 0, count);
indexes = newIndexes;
}
}
其他和堆相关的问题
1、使用堆来实现优先队列
动态选择优先级最高的任务执行
2、实现多路归并排序
将整个数组分成n个子数组,子数组排完序之后,将每个子数组中最小的元素取出,放到一个最小堆里面,每次从最小堆里取出最小值放到归并结束的数组中,被取走的元素属于哪个子数组,就从哪个子数组中再取出一个补充到最小堆里面,如此循环,直到所有子数组归并到一个数组中。