堆的实现及其应用
本篇文章记述的是堆排序,这个名字看起来好像又要介绍一个排序算法,但是排序算法是次要的,主要的是一个数据结构——堆。堆排序问题就是堆这种数据结构所衍生出来的一个应用,我们先了解一下优先队列的概念。普通的队列就是满足先进先出、后进后出的一个结构。那么优先级队列呢?出队顺序和入队顺序无关,和优先级相关,这就比如在医院看病,肯定是急诊病人优先看病。
优先级队列的应用
在操作系统中就会用到优先级队列,操作系统要同时执行多个任务,实际上操作系统是将CPU的执行周期划分为时间片,在每个时间片里只能执行一个任务,那么执行哪个任务呢?那就需要根据任务的优先级动态地选择优先级最高的任务来执行。
如何实现一个优先级队列呢?方法有很多,但是用堆来实现是最直接、最高效的。这是因为,堆和优先级队列非常相似。一个堆就可以看作一个优先级队列。很多时候,它们只是概念上的区分而已。往优先级队列中插入一个元素,就相当于往堆中插入一个元素;从优先级队列中取出优先级最高的元素,就相当于取出堆顶元素。 优先级队列的应用场景非常多。赫夫曼编码、图的最短路径、最小生成树算法很多数据结构和算法都要依赖于优先级队列。
堆的定义及其特点
堆是一种特殊的树。我们现在就来看看,什么样的树才是堆。我罗列了两点要求,只要满足这两点,它就是一个堆。
- 堆是一个完全二叉树;
- 堆中每一个节点的值都必须大于等于(或小于等于)其子树中每个节点的值。
第一点,堆必须是一个完全二叉树。完全二叉树要求,除了最后一层,其他层的节点个数都是满的,最后一层的节点都靠左排列。
第二点,堆中的每个节点的值必须大于等于(或者小于等于)其子树中每个节点的值。实际上,我们还可以换一种说法,堆中每个节点的值都大于等于(或者小于等于)其左右子节点的值。这两种表述是等价的。
对于每个节点的值都大于等于子树中每个节点值的堆,我们叫作“大堆”。对于每个节点的值都小于等于子树中每个节点值的堆,我们叫作“小堆”。
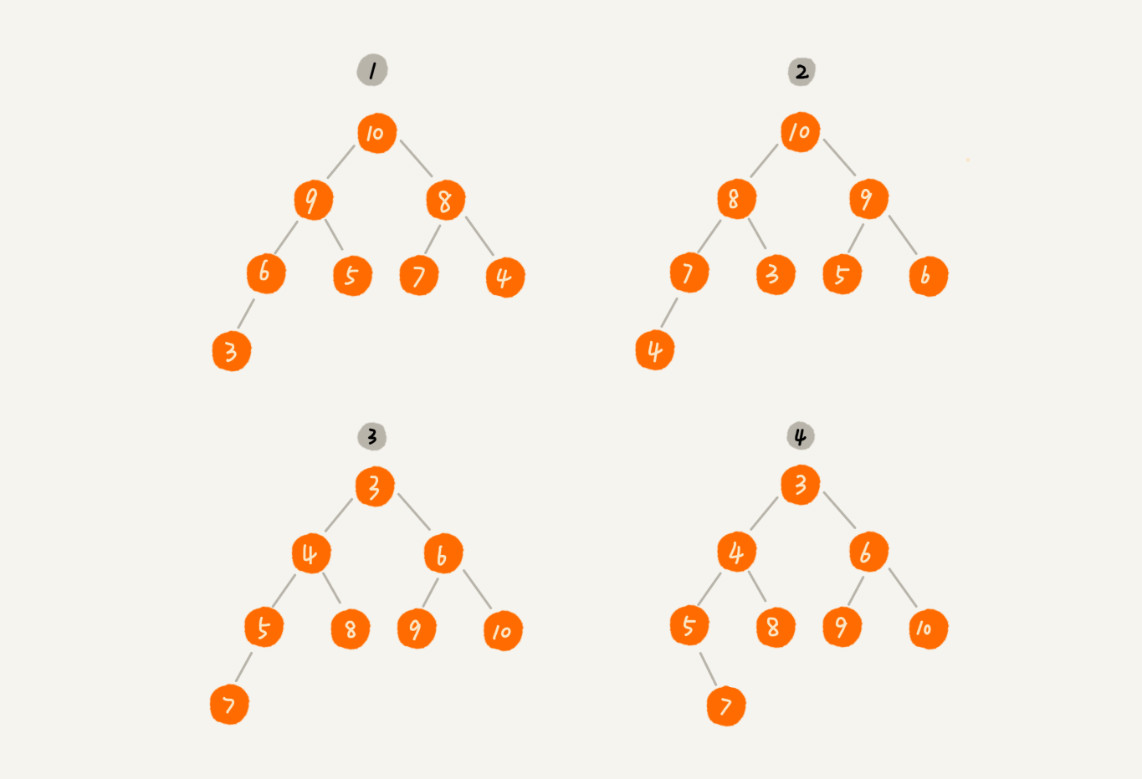
对于上图,1和2都是大堆;3是个小堆,而4不是堆。
完全二叉树比较适合用数组来存储。用数组来存储完全二叉树是非常节省存储空间的。因为我们不需要存储左右子节点的指针,单纯地通过数组的下标,就可以找到一个节点的左右子节点和父节点。 如下图所示:
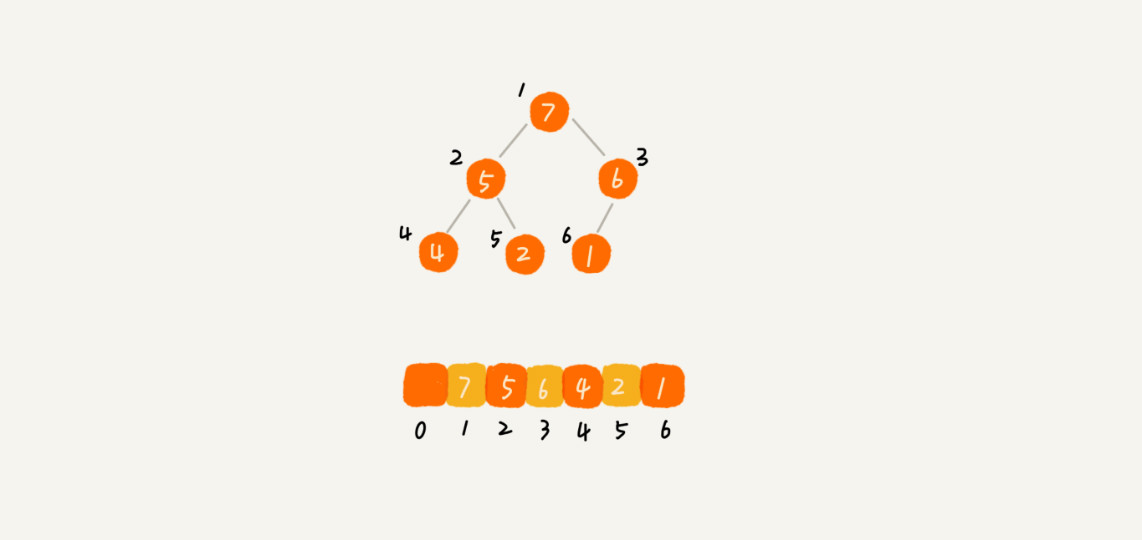
我们不难发现,这样的结构蕴含的规律是:左孩子在数组中的坐标是父节点的二倍,而右孩子在数组中的坐标是父节点的二倍加一。但是数组的索引却是从0开始的,堆的一个经典的实现就是数组0号位置空着,则parent (i) = i / 2(这里的除法是计算机除法,即取整),left child (i) = 2 * i,right child (i) = 2 * i +1。
堆的具体代码实现
根据上述的堆这种数据结构的,我们可以先实现下面的基础框架代码:
public class MaxHeap {
private int[] data;
//堆里有多少元素
private int count;
//因为0号位置不使用,所以capacity + 1
public MaxHeap(int capacity) {
data = new int[capacity + 1];
count = 0;
}
public int size(){
return count;
}
public boolean isEmpty(){
return count == 0;
}
}
接下来需要关注的焦点是如何向上调堆,我们在向堆中添加新的元素的时候,其实是向数组的末尾添加了一个新的元素,但是往堆中插入一个元素后,我们需要继续满足堆的两个特性。如果我们把新插入的元素直接放到堆的最后,是不是不符合堆的特性了? 于是我们就需要进行调整,让其重新满足堆的特性,这个过程叫做堆化:
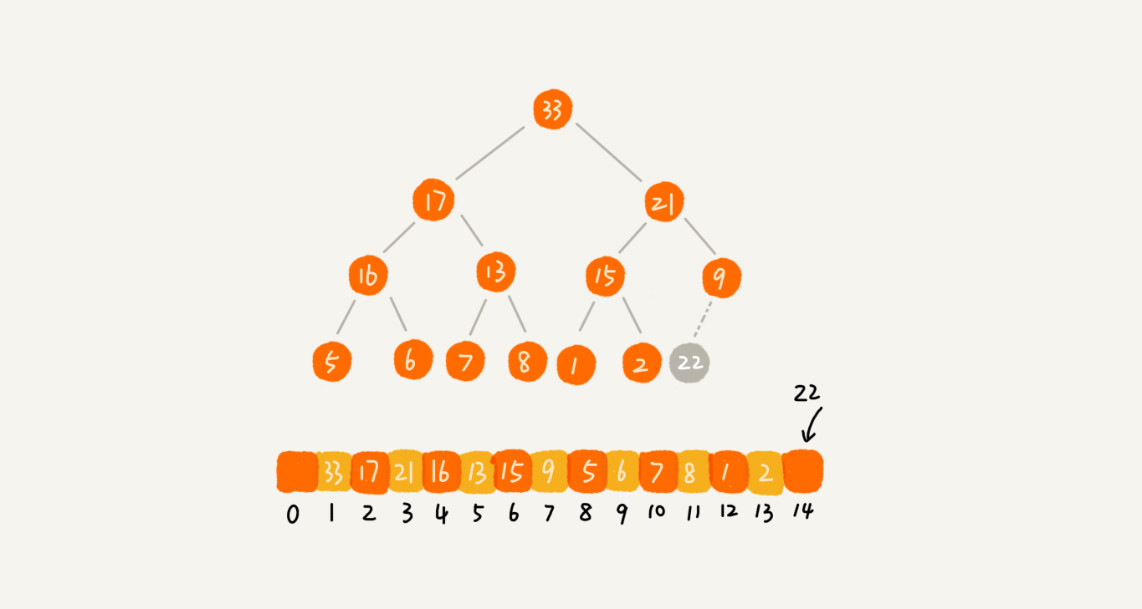
堆的调整方式有两种:向上调堆和向下调堆!在这里我们可以先看看向上调堆。
向上调堆(插入元素)
其实向上调堆的过程比较简单,那就是逐步和自己的父节点进行比较,如果不满足规则就交换即可,如下图:
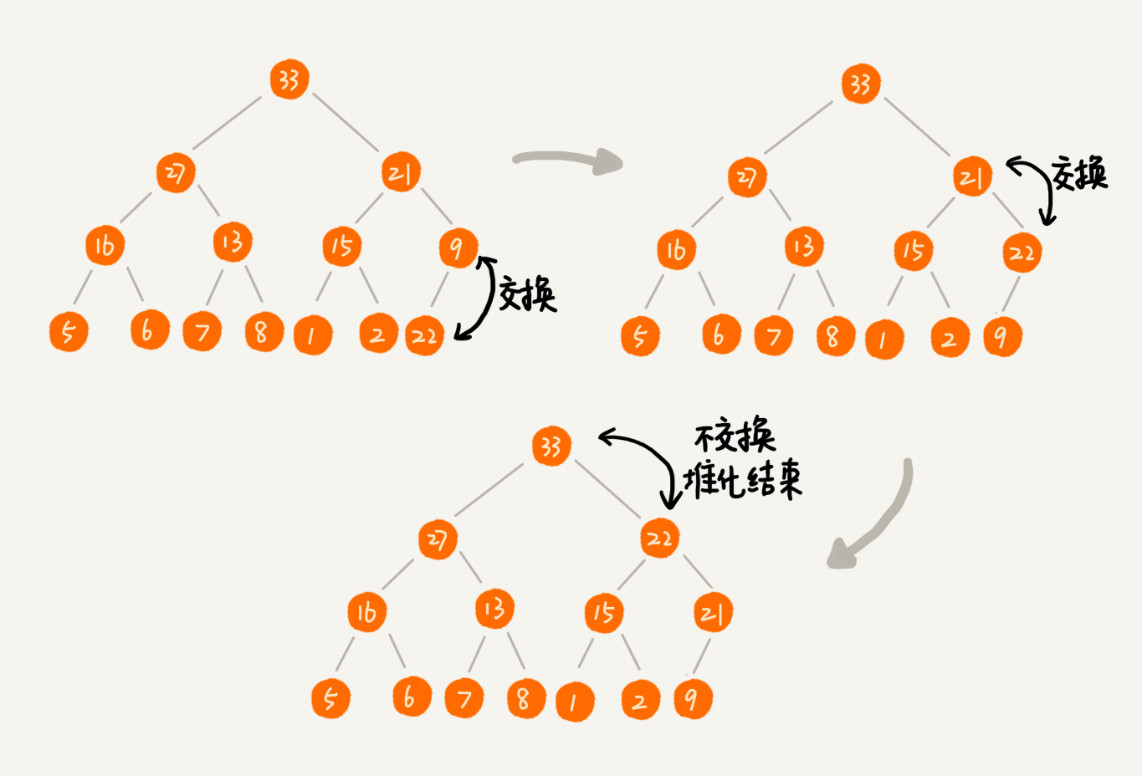
public class MaxHeap {
protected int[] data;
//堆里有多少元素
protected int count;
//堆的容量
protected int capacity;
//因为0号位置不使用,所以capacity + 1
public MaxHeap(int capacity) {
data = new int[capacity + 1];
count = 0;
this.capacity = capacity;
}
//获取现存元素个数
public int size(){
return count;
}
//判断是否为空
public boolean isEmpty(){
return count == 0;
}
//插入数据
public void insert(int item){
//判断容量知否超出
if(count + 1 >= capacity){
//开始扩容
resize();
}
//先存储到末尾
data[count + 1] = item;
count++;
//开始调堆
shiftUp(count);
}
//向上调堆
private void shiftUp(int k) {
while(k > 1 && data[k / 2] < data[k]){
swap(k/2, k);
k /= 2;
}
}
//交换对应两个位置的值
private void swap(int i, int j){
int tmp = data[i];
data[i] = data[j];
data[j] = tmp;
}
//扩充容量
private void resize() {
int[] newData = new int[capacity * 2];
System.arraycopy(data, 0, newData, 0, count);
data = newData;
capacity *= 2;
}
}
上面就是这个堆的实现,而且这个堆拥有扩容的功能。为了在控制台打印方便观察,实现一个打印堆的功能(数字太多控制台容易乱掉,所以限定在100个元素之内):
public class PrintableMaxHeap extends MaxHeap {
public PrintableMaxHeap(int capacity){
super(capacity);
}
// 以树状打印整个堆结构
public void treePrint(){
if( size() >= 100 ){
System.out.println("This print function can only work for less than 100 integer");
return;
}
System.out.println("The max heap size is: " + size());
System.out.println("Data in the max heap: ");
for( int i = 1 ; i <= size() ; i ++ ){
// 我们的print函数要求堆中的所有整数在[0, 100)的范围内
assert data[i] >= 0 && data[i] < 100;
System.out.print(data[i] + " ");
}
System.out.println();
System.out.println();
int n = size();
int maxLevel = 0;
int numberPerLevel = 1;
while( n > 0 ){
maxLevel += 1;
n -= numberPerLevel;
numberPerLevel *= 2;
}
int maxLevelNumber = (int)Math.pow(2, maxLevel-1);
int curTreeMaxLevelNumber = maxLevelNumber;
int index = 1;
for( int level = 0 ; level < maxLevel ; level ++ ){
String line1 = new String(new char[maxLevelNumber*3-1]).replace('\0', ' ');
int curLevelNumber = Math.min(count-(int)Math.pow(2,level)+1,(int)Math.pow(2,level));
boolean isLeft = true;
for( int indexCurLevel = 0 ; indexCurLevel < curLevelNumber ; index ++ , indexCurLevel ++ ){
line1 = putNumberInLine(data[index] , line1 , indexCurLevel , curTreeMaxLevelNumber*3-1 , isLeft );
isLeft = !isLeft;
}
System.out.println(line1);
if( level == maxLevel - 1 )
break;
String line2 = new String(new char[maxLevelNumber*3-1]).replace('\0', ' ');
for( int indexCurLevel = 0 ; indexCurLevel < curLevelNumber ; indexCurLevel ++ )
line2 = putBranchInLine( line2 , indexCurLevel , curTreeMaxLevelNumber*3-1 );
System.out.println(line2);
curTreeMaxLevelNumber /= 2;
}
}
private String putNumberInLine( Integer num, String line, int indexCurLevel, int curTreeWidth, boolean isLeft){
int subTreeWidth = (curTreeWidth - 1) / 2;
int offset = indexCurLevel * (curTreeWidth+1) + subTreeWidth;
assert offset + 1 < line.length();
if( num >= 10 )
line = line.substring(0, offset+0) + num.toString()
+ line.substring(offset+2);
else{
if( isLeft)
line = line.substring(0, offset+0) + num.toString()
+ line.substring(offset+1);
else
line = line.substring(0, offset+1) + num.toString()
+ line.substring(offset+2);
}
return line;
}
private String putBranchInLine( String line, int indexCurLevel, int curTreeWidth){
int subTreeWidth = (curTreeWidth - 1) / 2;
int subSubTreeWidth = (subTreeWidth - 1) / 2;
int offsetLeft = indexCurLevel * (curTreeWidth+1) + subSubTreeWidth;
assert offsetLeft + 1 < line.length();
int offsetRight = indexCurLevel * (curTreeWidth+1) + subTreeWidth + 1 + subSubTreeWidth;
assert offsetRight < line.length();
line = line.substring(0, offsetLeft+1) + "/" + line.substring(offsetLeft+2);
line = line.substring(0, offsetRight) + "\\" + line.substring(offsetRight+1);
return line;
}
}
接下来测试一下是否成功:
public class MaxHeapTest {
public static void main(String[] args) {
PrintableMaxHeap maxHeap = new PrintableMaxHeap(10);
for (int i = 0; i < 15; i++) {
maxHeap.insert((int)(Math.random() * 100));
}
maxHeap.treePrint();
}
}
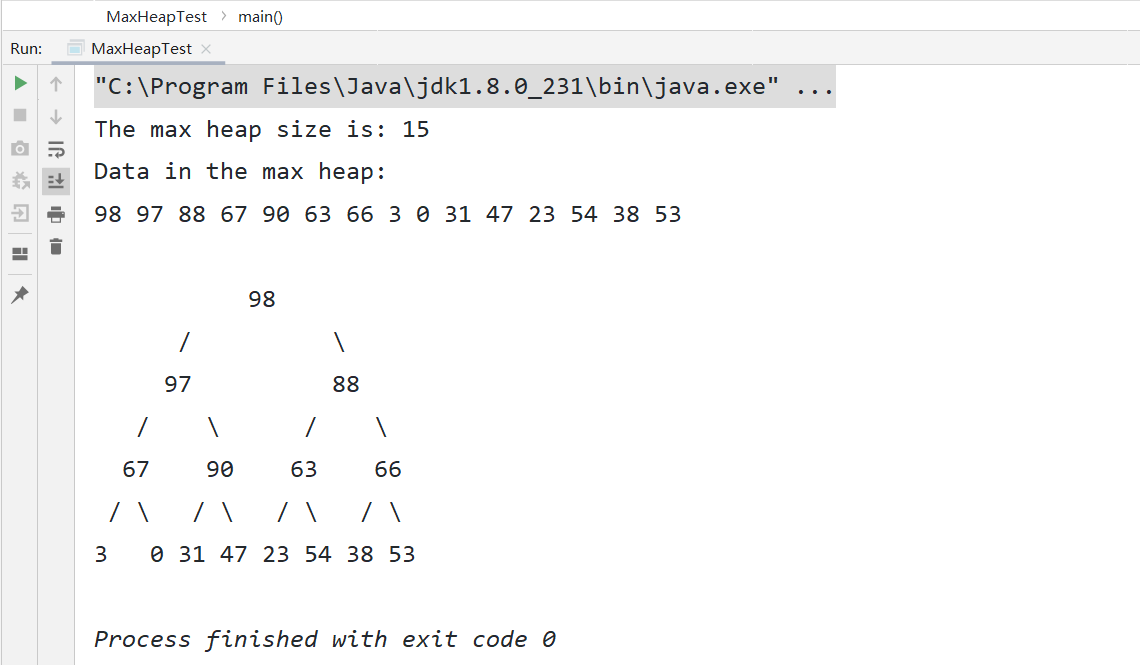
可以看出,我们不断插入数据的时候其实就是不断调堆的过程。
向下调堆(取出元素)
取出堆顶元素,任然需要维持堆的特性,所以我们只把最后一个节点放到堆顶,然后利用同样的父子节点对比方法。对于不满足父子节点大小关系的,互换两个节点,并且重复进行这个过程,直到父子节点之间满足大小关系为止。这就是从上往下的堆化方法,也叫做向下调堆。
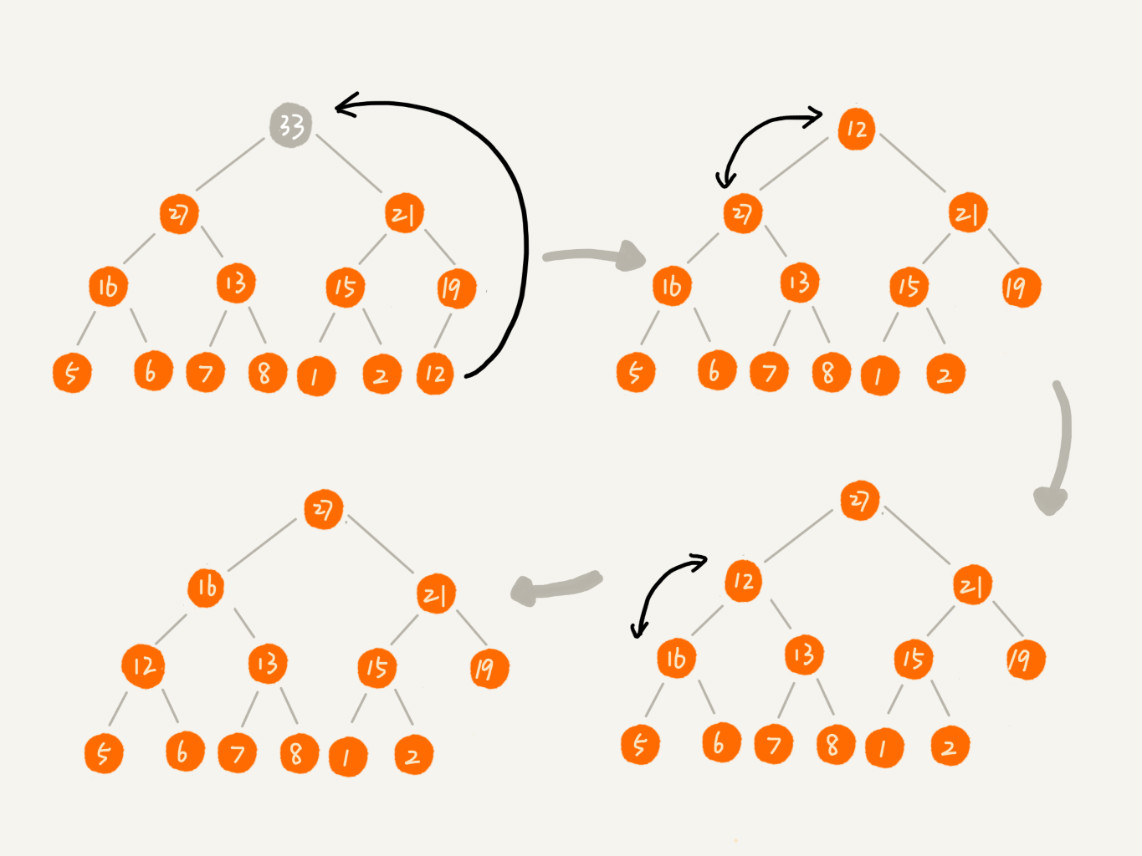
所以整个堆的代码如下:
public class MaxHeap {
protected int[] data;
//堆里有多少元素
protected int count;
//堆的容量
protected int capacity;
//因为0号位置不使用,所以capacity + 1
public MaxHeap(int capacity) {
data = new int[capacity + 1];
count = 0;
this.capacity = capacity;
}
//获取现存元素个数
public int size(){
return count;
}
//判断是否为空
public boolean isEmpty(){
return count == 0;
}
//插入数据
public void insert(int item){
//判断容量知否超出
if(count + 1 >= capacity){
//开始扩容
resize();
}
//先存储到末尾
data[count + 1] = item;
count++;
//开始向上调堆
shiftUp(count);
}
//向上调堆
private void shiftUp(int k) {
while(k > 1 && data[k / 2] < data[k]){
swap(k/2, k);
k /= 2;
}
}
//取出数据
public int extractMax(){
if(count == 0) throw new RuntimeException("Heap is null");
int ret = data[1];
swap(1, count);
count--;
//开始向下调堆
shiftDown(1);
return ret;
}
//向下调堆
private void shiftDown(int k) {
while (2 * k <= count){
int j = 2 * k; //在此轮循环中,data[k]和data[j]交换位置
if(j + 1 <= count && data[j+1] > data[j]){
j++;
}
if(data[k] >= data[j]){
break;
}
swap(k, j);
k = j;
}
}
//交换对应两个位置的值
private void swap(int i, int j){
int tmp = data[i];
data[i] = data[j];
data[j] = tmp;
}
//扩充容量
private void resize() {
int[] newData = new int[capacity * 2];
System.arraycopy(data, 0, newData, 0, count);
data = newData;
capacity *= 2;
}
}
一个包含n个节点的完全二叉树,树的高度不会超过logn。堆化的过程是顺着节点所在路径比较交换的,所以堆化的时间复杂度跟树的高度成正比,也就是O(logn)。插入数据和删除堆顶元素的主要逻辑就是堆化,所以往堆中插入一个元素和删除堆顶元素的时间复杂度都是O(logn)。
堆排序与heapify建堆
我们通过堆的插入操作把数组中的元素逐个插入到堆中,然后逐个取出堆顶元素防区数组中(如果是大堆从后往前放置即可)。堆排序不是稳定的排序算法,因为在排序的过程,存在将堆的最后一个节点跟堆顶节点互换的操作,所以就有可能改变值相同数据的原始相对顺序。
public class HeapSort {
public static void heapSort(int[] arr){
MaxHeap maxHeap = new MaxHeap(arr.length);
for (int i = 0; i < arr.length; i++) {
maxHeap.insert(arr[i]);
}
for (int i = arr.length - 1; i >= 0; i--) {
arr[i] = maxHeap.extractMax();
}
}
}
我们进行排序的时候,首先得把数组中的元素逐个插入到堆中,这种建堆思路的处理过程是从前往后处理数组数据,并且每个数据插入堆中时,都是从下往上堆化。但是有没有一种无需插入操作,直接把数组变成堆的方法呢?其实是有的:
因为叶子节点往下堆化只能自己跟自己比较,所以我们直接从第一个非叶子节点开始,依次堆化就行了。 非叶子节点其实很容易找出来,元素个数除以二即是第一个非叶子节点,如下图9个元素,4号即是第一个非叶子节点:
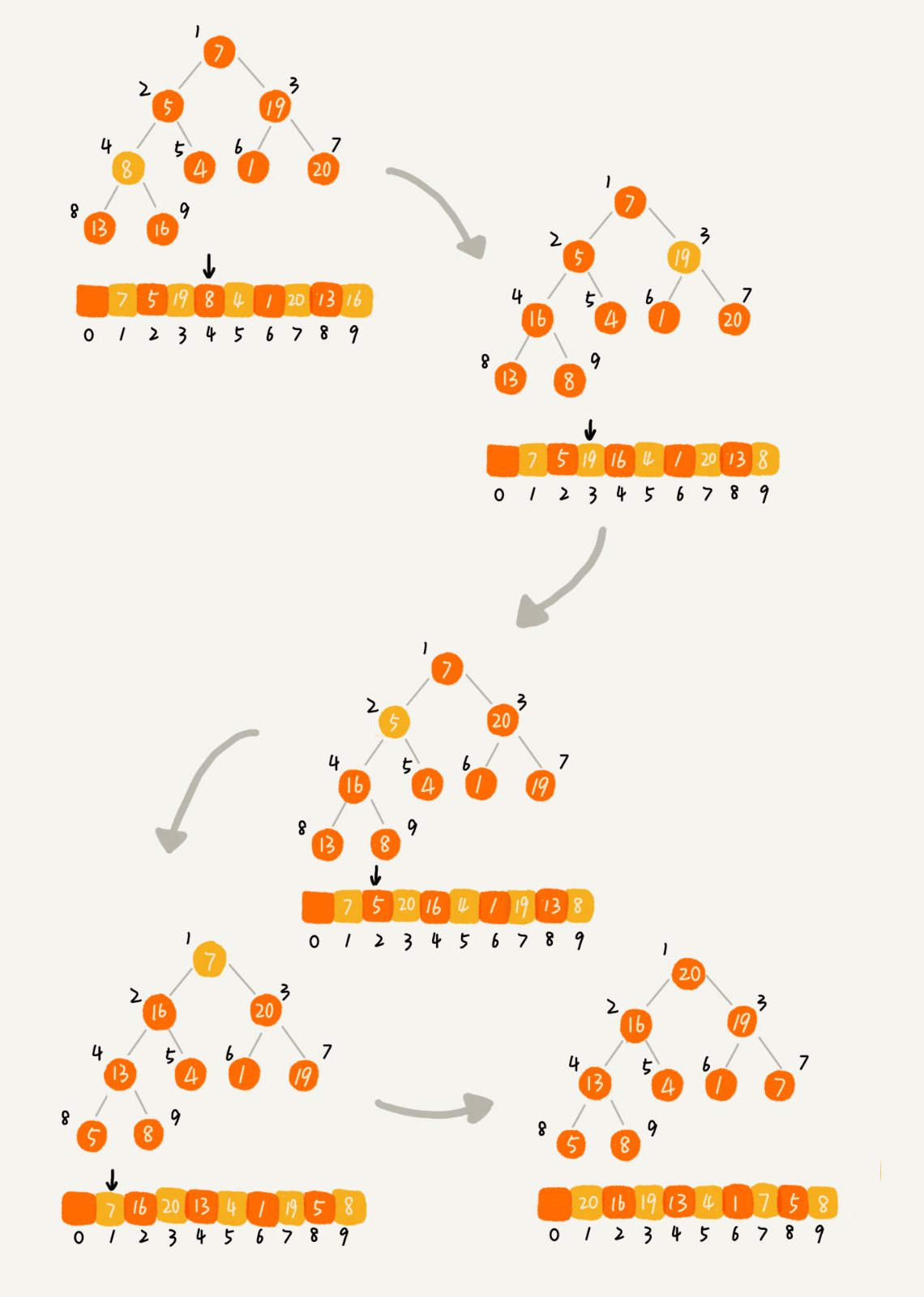
所以我们需要加入这样一个构造方法:
public class MaxHeap {
...
public MaxHeap(int[] arr){
data = new int[arr.length + 1];
capacity = arr.length + 1;
for (int i = 0; i < arr.length; i++) {
data[i + 1] = arr[i];
}
count = arr.length;
//从第一个不是叶子节点的位置开始
for (int i = count / 2; i >= 1; i--) {
shiftDown(i);
}
}
...
}
将n个元素逐个插入到堆中,这个操作的时间复杂度是O(nlogn),而heapify建堆的时间复杂度为O(n)。
原地堆排序
其实堆排序完全可以变成一个原地排序算法,直接在数组上进行。因为堆的经典实现就是从1号位置开始,但是我们现在要实现的是原地排序的算法,规律完全相同,只是规律的表达式稍微有所不同。因为在上面的堆排序算法中,都需要先将数组中的元素放到堆中,然后再把堆中的元素取出来。整个程序中又额外的开辟了n个空间,事实上我们通过上面的理论方法,完全可以使一个数组在原地完成堆排序,而不需要任何的额外空间:
我们可以应用之前讲到的堆化(heapify)是我们的数组构建成一个最大堆。在这个最大堆中第一个元素就是这个数组的最大值:

最后一个非叶子节点的索引:(count - 2)/ 2、
parent(i) = (i - 1) / 2、left child (i) = 2 * i +1、right child (i) = 2 * i +2
public class HeapSort {
public static void heapSort_03(int[] arr){
//heapify
for (int i = (arr.length - 1)/2; i >= 0; i--) {
shiftDown(arr, arr.length, i);
}
for (int i = arr.length - 1; i > 0; i--) {
swap(arr, 0, i);
shiftDown(arr, i, 0);
}
}
private static void shiftDown(int[] arr, int length, int k) {
while (2 * k + 1 < length){
int j = 2 * k + 1;
if(j + 1 < length && arr[j+1] > arr[j]){
j++;
}
if(arr[k] >= arr[j]){
break;
}
swap(arr, k, j);
k = j;
}
}
private static void swap(int[] arr, int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
}