快速排序及其优化
快速排序(Quick Sort)被称为20世纪对世界影响最大的算法之一,现在我们来看快速排序算法,习惯性把它简称为快排,快排利用的也是分治思想。乍看起来,它有点像归并排序,但是思路其实完全不一样。现在,我们先来看下快排的核心思想,最后将讲述快速排序的两个优化方案,其实还有一种三路快排的优化方案也是可以的,但是本片文章重点在于快速排序的原理和实现,所以三路快排的优化方案不会出现在这篇文章里,以后再详细记录一下。
快速排序(QuickSort)原理
快排的思想是这样的:如果要排序数组中下标从 p到 r之间的一组数据,我们选择p到r之间的任意一个数据作为pivot(分区点),我们遍历p到r之间的数据,将小于pivot的放到左边,将大于pivot的放到右边,将pivot放到中间。经过这一步骤之后,数组p到r之间的数据就被分成了三个部分,前面p到q-1之间都是小于pivot的,中间是pivot,后面的q+1到r之间是大于pivot的。
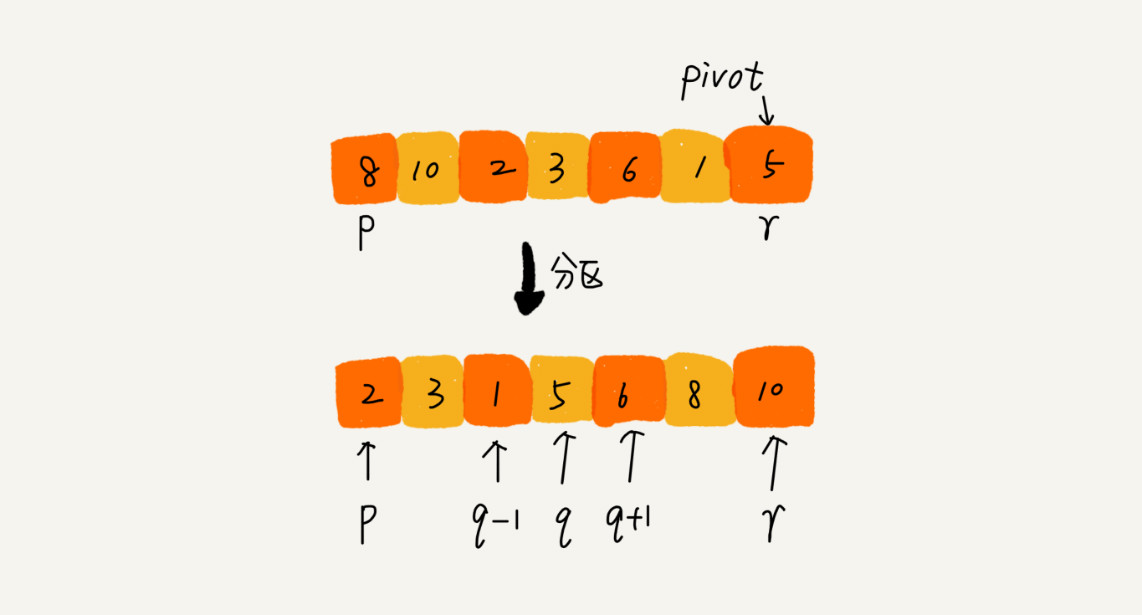
根据分治、递归的处理思想,我们可以用递归排序下标从p到q-1之间的数据和下标从q+1到r之间的数据,直到区间缩小为 1,就说明所有的数据都有序了。
public static void quickSort(int[] arr){
quickSortChild(arr, 0, arr.length - 1);
}
//对arr[start... end]部分进行快速排序
private static void quickSortChild(int[] arr, int start, int end){
if(start >= end) return;
int p = partition(arr, start, end);
quickSortChild(arr, start, p - 1);
quickSortChild(arr, p + 1, end);
}
/**
* 将arr[start...end]部分进行partition操作
* 返回p,使得arr[start...p-1] < arr[p]; arr[p+1...end] > arr[p]
*/
private static int partition(int[] arr, int start, int end) {
int v = arr[start]; //取第一个元素作为基准值
//arr[start+1...j] < v; arr[j+1...i) > v
int j = start;
int tmp;
for (int i = start + 1; i <= end ; i++) {
if(arr[i] < v){
tmp = arr[j + 1];
arr[j + 1] = arr[i];
arr[i] = tmp;
j++;
}
}
tmp = arr[start];
arr[start] = arr[j];
arr[j] = tmp;
return j;
}
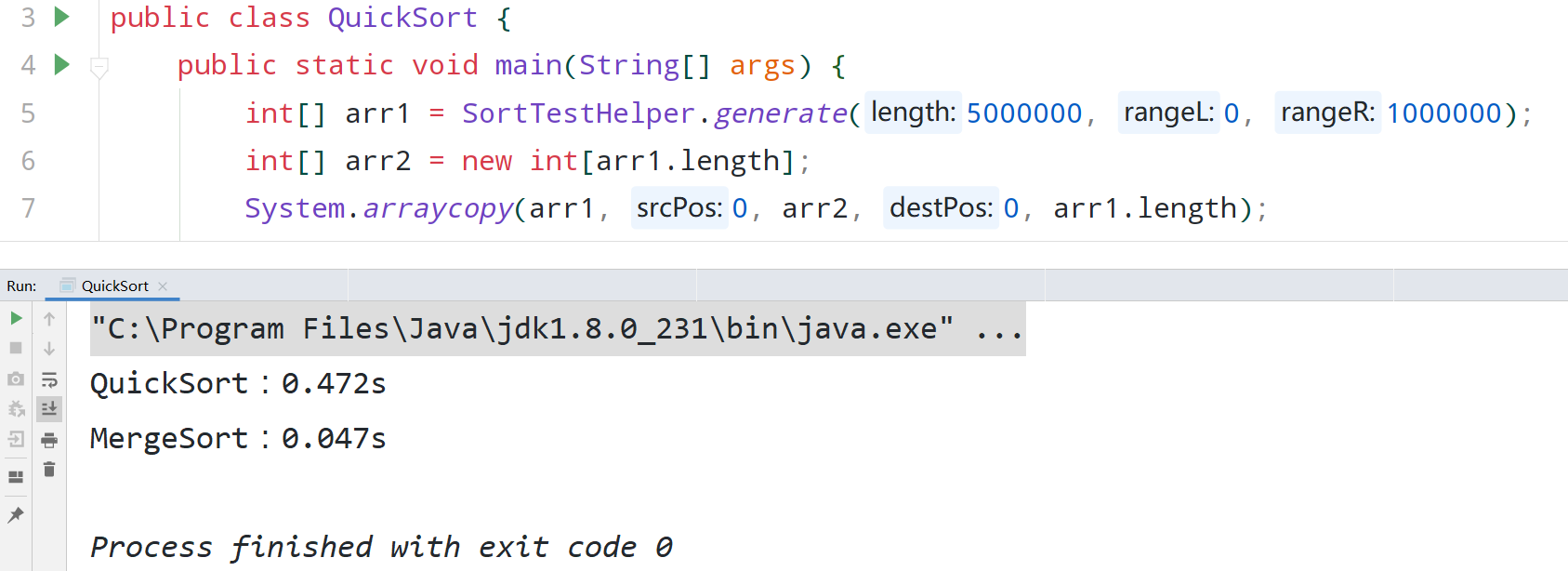
现在测试一下快速排序和归并排序的效率,排500万个完全随机数快排比归并排序快10倍左右:
快速排序核心 partition
我们重点需要关注的是partition函数,我们知道快排无非就是找个基准点,然后把小于基准点的放在左边,大于基准点的放在右边,partition过程就是需要进行如下操作的过程:

关键是如何把小的元素放前面,大的放后面呢?
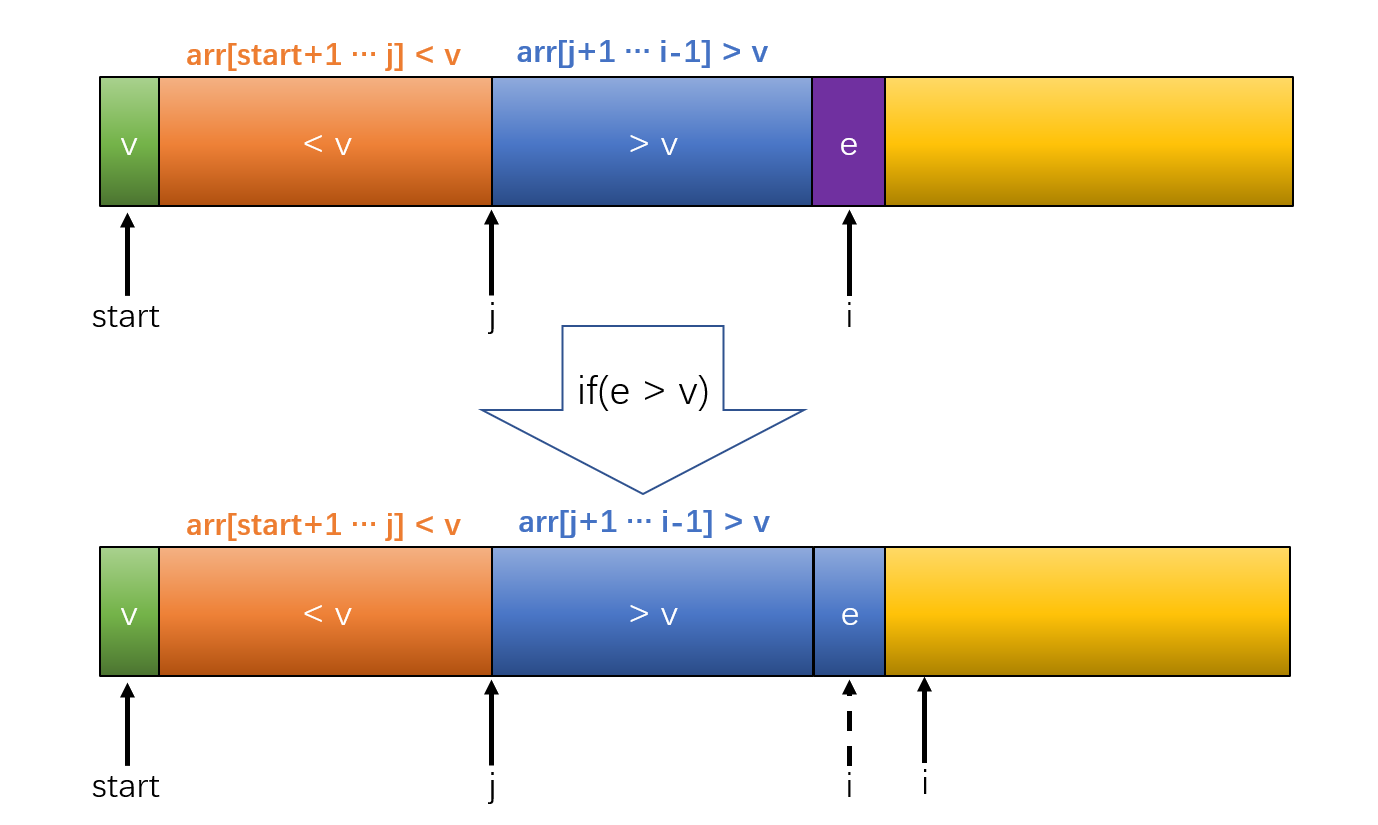
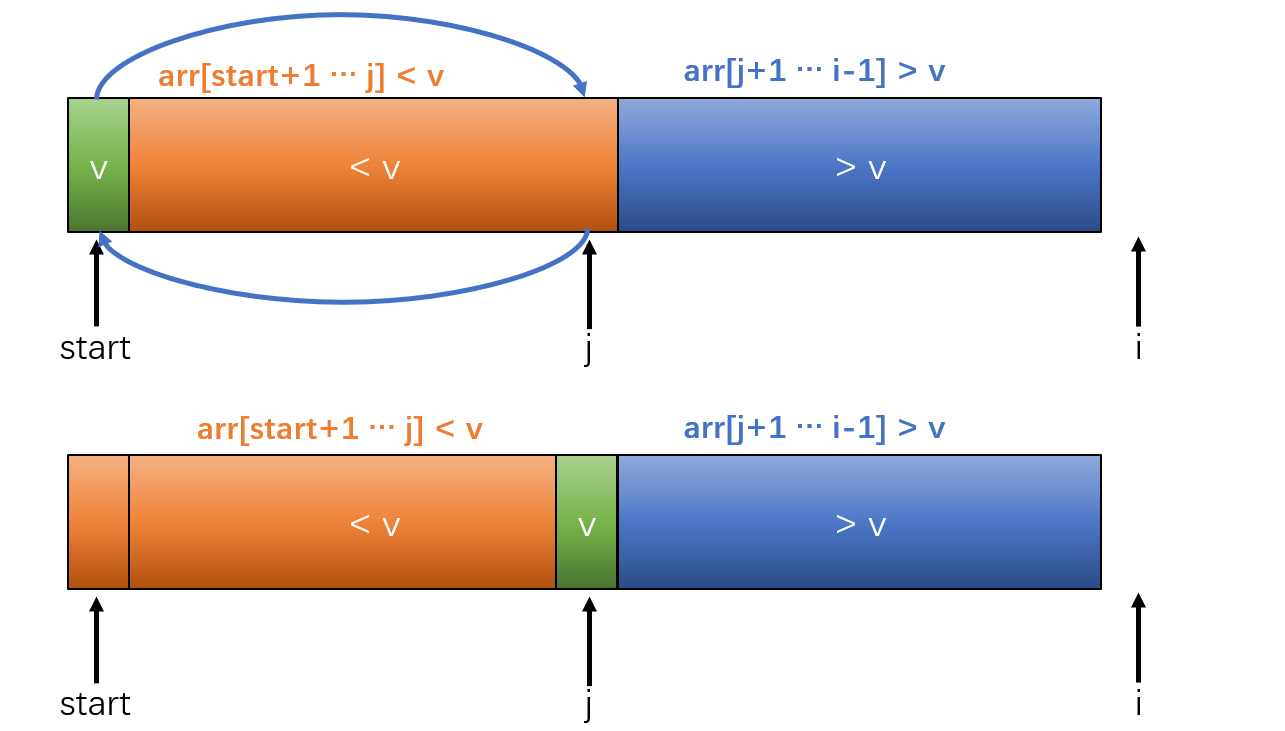
我们可以假设上面的这一种情况,以第一次元素作为基准值,大于V的放后面,小于v的放前面,j作为分隔位置的坐标,现在到了该判断e是大于v还是小于v的时候了,如果e大于v,那么很容易,就如上图所示,只需要把e给并入到蓝色部分中即可,然后i++,去判断下一个元素是否大于或者小于v。
那么如果e小于v呢?应该如何调整呢?
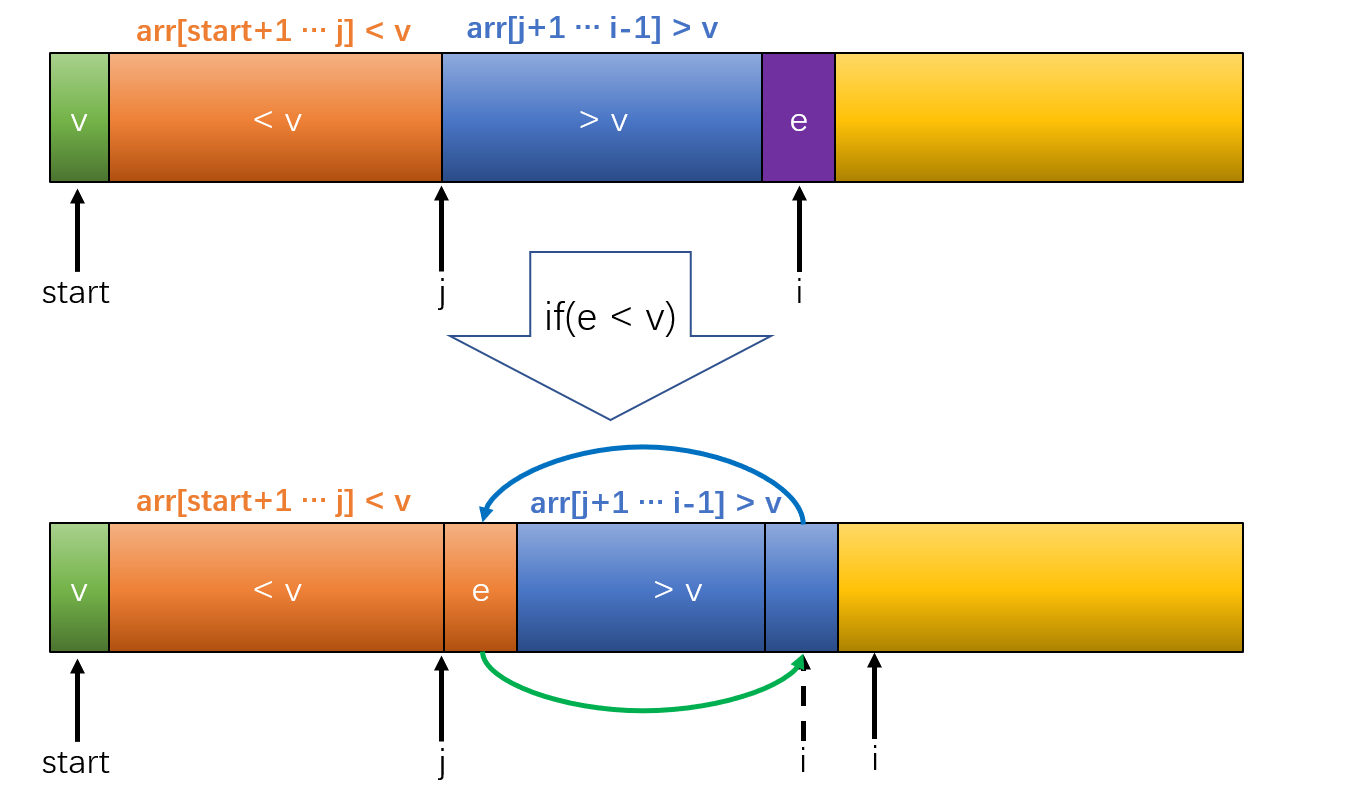
其实也很简单,只需要让蓝色部分(也就是大于基准值的那一部分)的第一个元素与e的位置交换,这样剩下的步骤就是把j++(即移动分界位置坐标),然后i++,去判断下一个元素是否大于或者小于v。
当上述步骤完成后,只需要把v和橙色部分的最后一个元素交换位置即可,这样便使得v前面的元素比它小,后面的元素比它大,于是我们就成功的把一个数组给分成了两组,并且只需要把基准值的坐标给返回了。
快速排序的优化(随机化)
其实第一中优化方式和之前一致,那就是在递归到数据规模比较小的时候用直接插入排序,这样可以稍微提高一些效率,但是这个优化不是我们现在优化的重点:
...
//对arr[start... end]部分进行快速排序
private static void quickSortChild(int[] arr, int start, int end){
//if(start >= end) return;
//优化点:在递归到数据规模比较小的时候就用插入排序
if(end - start <= 15){
insertionSort(arr, start, end);
return;
}
int p = partition(arr, start, end);
quickSortChild(arr, start, p - 1);
quickSortChild(arr, p + 1, end);
}
...
之前通过对完全随机数进行排序测试,我们发现快排比归并排序快十倍左右,现在我们需要测试一下对近乎有序的数组进行排序结果又是怎样的,我们对500000个数字进行随机位置10次交换,对比一下和归并排序的效率:
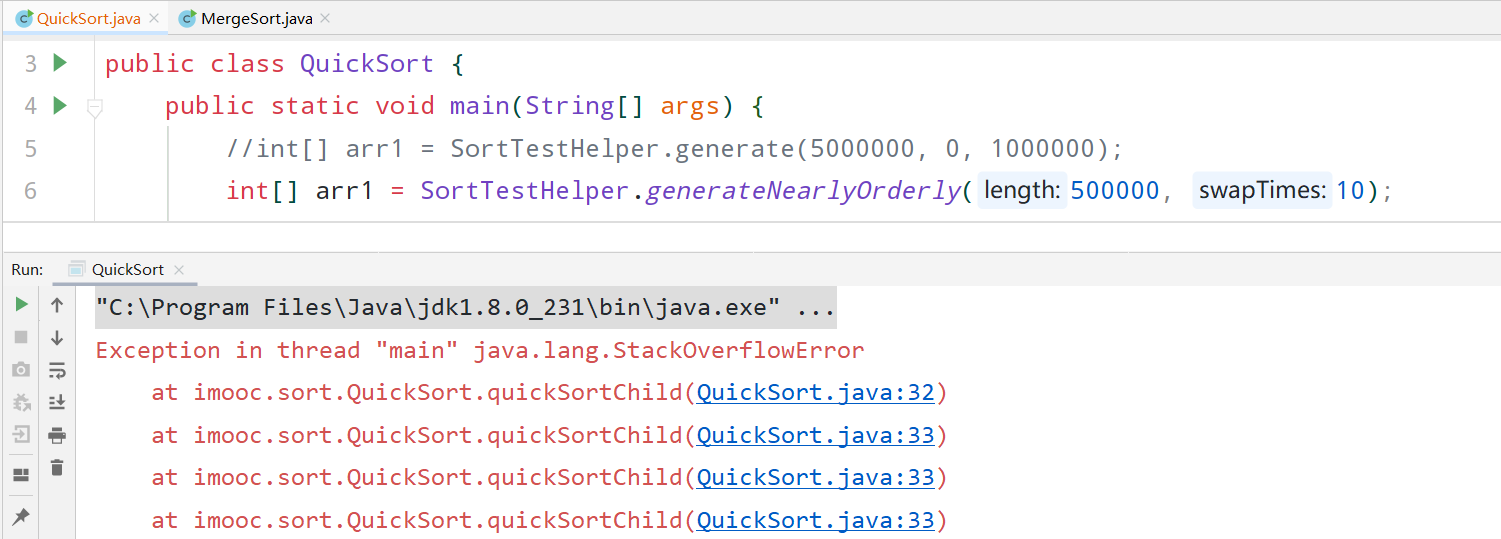
结果栈溢出了,这是因为我们几乎每次都找的是第一个元素作为基准值,所以导致了栈溢出。可以先回想一下,为什么归并排序的时间复杂度能稳定在nlogn呢?其实很简单,因为对于归并排序来讲,总是能将数据均等的一分为二,这是归并排序的原理图:
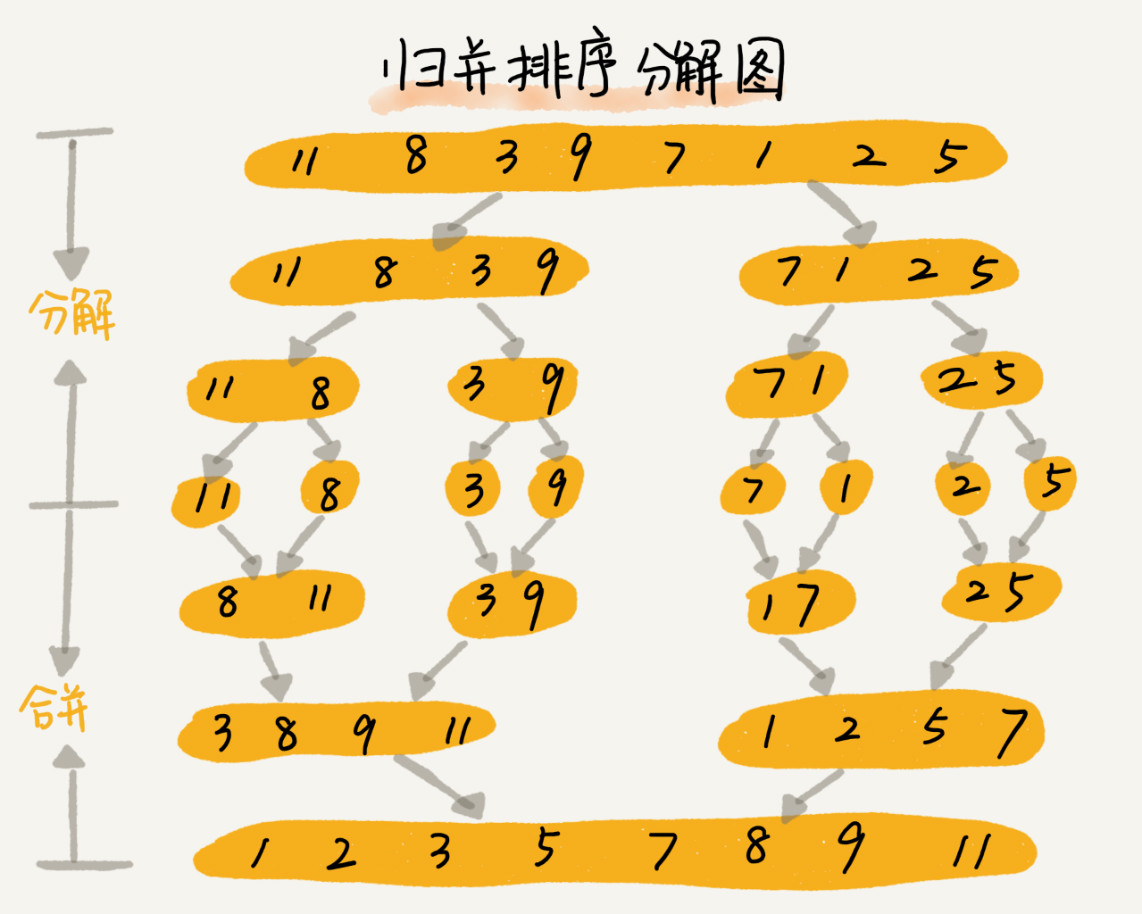
所以对于快速排序来说,明显并没有归并排序那么均等分配,于是乎在极端情况下,直接一个元素一组,剩下的所有元素一组,那么这样肯定是不符合我们预期要求的,上面的栈溢出的情况就是如下图,这就是快速排序最差的情况,在这种情况下,时间复杂度退化为O(n²)
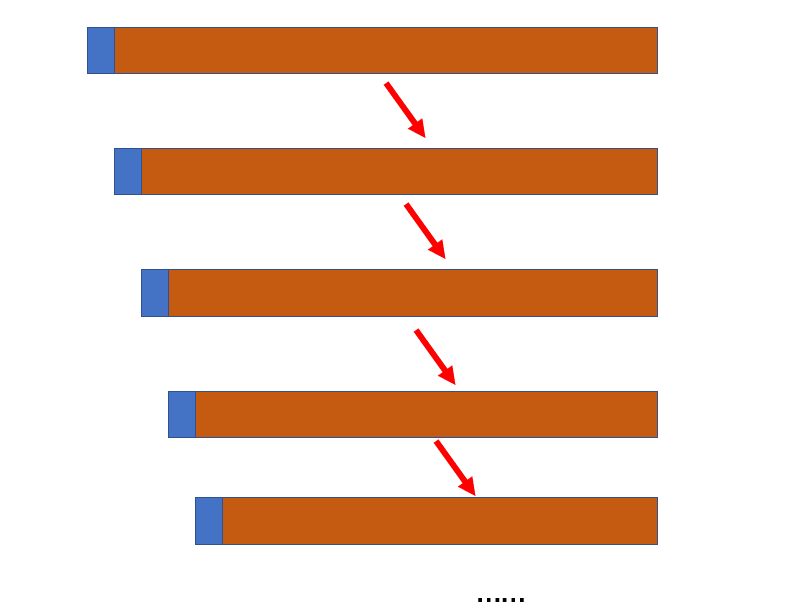
所以这就说明了我们不能直接把第一个元素当成基准值,那么基准值的位置如何确定呢?我们只需要随机基准值位置就好了,之前的代码不用修改,只需要把我们的随机位置的基准值和数组第一个元素做交换即可:
...
/**
* 将arr[start...end]部分进行partition操作
* 返回p,使得arr[start...p-1] < arr[p]; arr[p+1...end] > arr[p]
*/
private static int partition(int[] arr, int start, int end) {
//int v = arr[start]; //取第一个元素作为基准值
//优化点: 找个随机位置的元素和头元素交换
int randomIndex = (int)(Math.random() * 100) % (end - start + 1) + start;
int tmp = arr[randomIndex];
arr[randomIndex] = arr[start];
arr[start] = tmp;
int v = arr[start];
//arr[start+1...j] < v; arr[j+1...i) > v
int j = start;
for (int i = start + 1; i <= end ; i++) {
if(arr[i] < v){
tmp = arr[j + 1];
arr[j + 1] = arr[i];
arr[i] = tmp;
j++;
}
}
tmp = arr[start];
arr[start] = arr[j];
arr[j] = tmp;
return j;
}
...
快速排序的优化(双路快排)
上面只是快速排序遇到的第一种极端情况,接下来看看另一种情况,现在10万个数随机数,但是范围都是0-10之间的数字,意味着有很多重复的数字,这种情况下快速排序的表现怎么样呢?
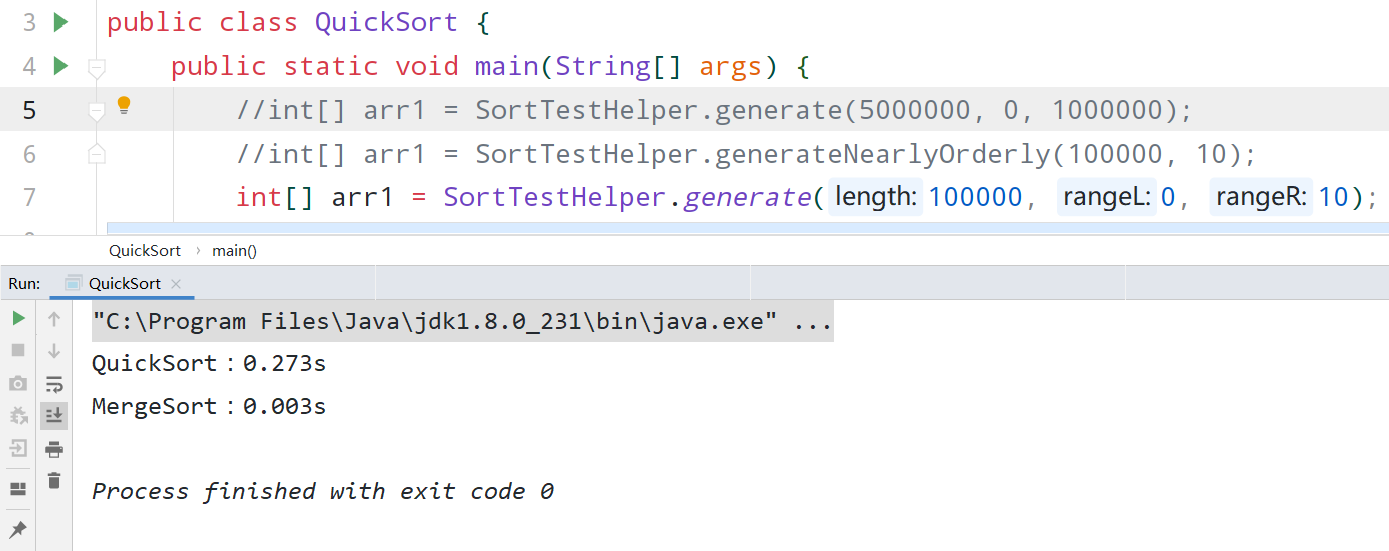
我们不难发现,快速排序又比规归并排序慢了,原因其实很简单:我们在partition函数中,把比基准值小的划到左边,比基准值大的划到右边,那么相等的呢?其实根据我们上面写的代码遇到相等的是划到右边的,所以当遇到很多重复元素的时候,本来nlogn的时间复杂度又变成近乎O(n²),那么划到左边行不行呢?其实也不行,因为即使把相等的划到左边在大规模相同的数据情况下还是同样面临极端情况,还是会退化到O(n²)。
以前我们在进行快速排序的时候总是把i++,直到累加到数组的末尾,现在我们只需要放在两头即可,小于基准值的放左边,大于基准值的放右边,两边同时开始向中间排:
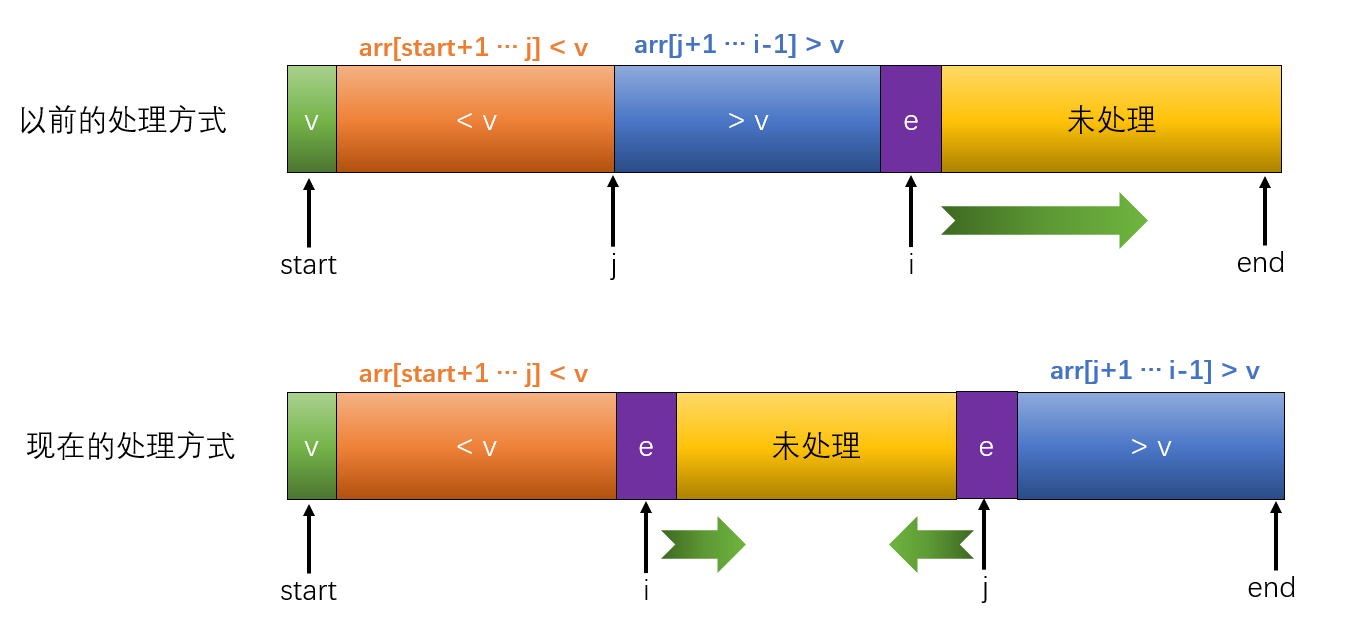
其实上图稍微有一点错误,那就是黄色部分是小于等于基准值的,蓝色部分是大于等于基准值的,我们看一下这个过程演示:
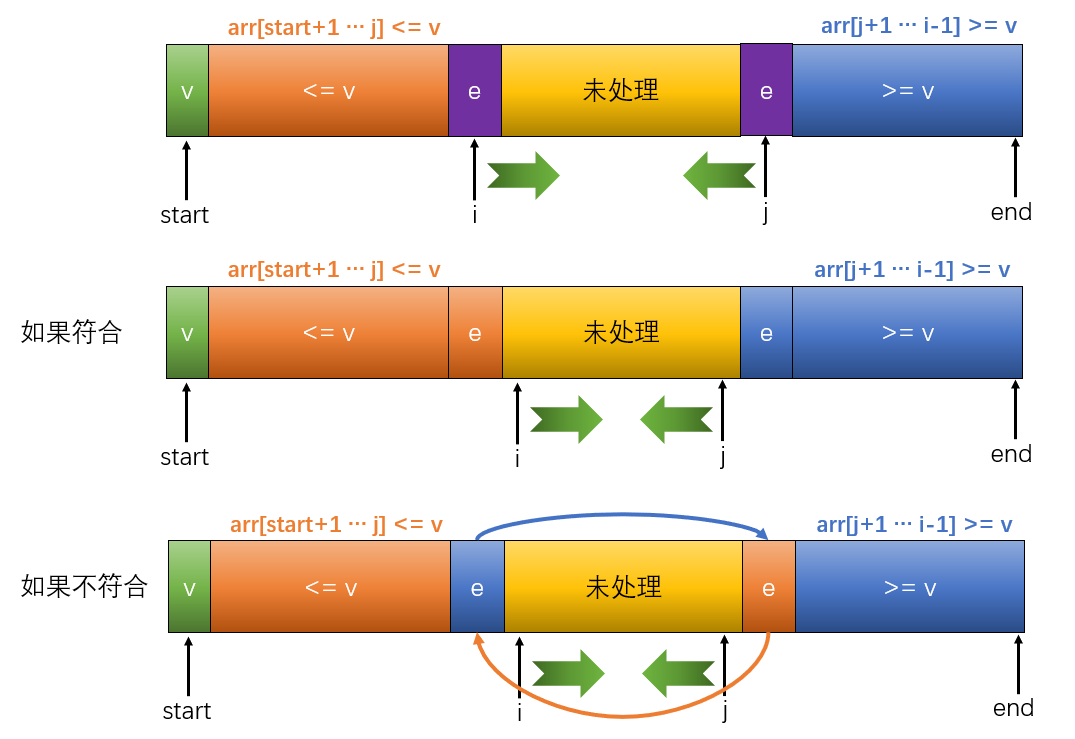
这样就解决了大量的重复元素集中在一端的情况,即使遇到了很多重复的元素也能将他们几乎平分开来。
...
private static int partition2(int[] arr, int start, int end) {
//随机位置基准值
int randomIndex = (int)(Math.random() * 100) % (end - start + 1) + start;
//和首元素交换
int tmp = arr[randomIndex];
arr[randomIndex] = arr[start];
arr[start] = tmp;
int v = arr[start];
// arr[start+1...i) <= v, arr(j...end] >= v
int i = start + 1, j = end;
while(true){
while(i <= end && arr[i] < v) i++;
while(j >= start +1 && arr[j] > v) j--;
if(i > j) break;
//swap(arr[i], arr[j])
tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
i++;
j--;
}
//swap(arr[start], arr[j])
tmp = arr[start];
arr[start] = arr[j];
arr[j] = tmp;
return j;
}
...