希尔排序是插入排序的一种，又称缩小增量排序，是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法，可以说它是插入排序的高级版。我们可以先回顾一下直接插入排序的过程：

排序前将第一个元素看成有序的数列

• 第1趟排序后：得到一个长度为2的有序数列
• 第2趟排序后：得到一个长度为3的有序数列
• 第3趟排序后：得到一个长度为4的有序数列
• ……..每趟插入排序，都可以将一个无序值插入一个有序数列，直到全部元素有序

最坏情况下，直接插入排序的时间复杂度是O(n²)。从上图可以看出，6这个元素被移动了三次才到末尾。我在直接插入排序的博客 《O(n²)的三个排序算法》 中写到，直接插入排序最好的情况就是本来就有序，所以直接插入排序用来排序那些近乎有序的数组是非常适合的。所以我们对于一个无序数组，先把它变成大致有序，然后超级大致有序，然后变成超级超级大致有序……最后变成完全有序，这样可以省略掉很多不必要的元素交换。

那么如何让大元素一开始就分批向后移动呢？那就是通过分组排序的方式， 应该怎么分呢？比如有10个元素的序列，分成几个才合适？每次缩减又是多少呢？ 将一个序列分成好几个序列，用一个数来表示：那个数称为增量，我们可以发现增量越来越小，其实就是数组越来越有序的过程。

下面来看看希尔排序的过程：

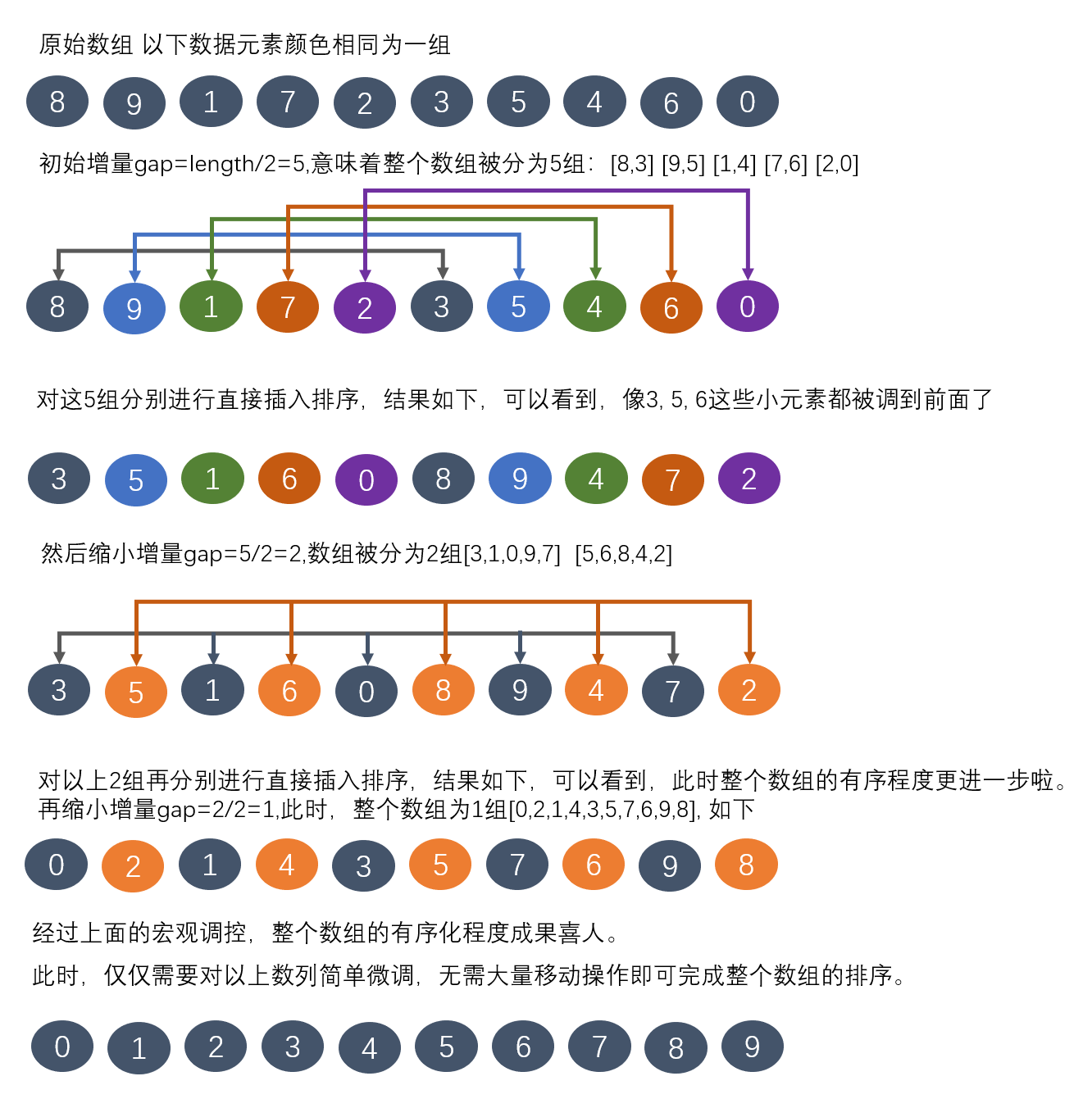
下面通过代码来实现一下希尔排序：

 1public static void shellSort(int[] arr){
 2    //每次都缩小增量
 3    for (int step = arr.length / 2; step > 0; step /= 2) {
 4        for (int i = step; i < arr.length; i++) {
 5            int j = i;
 6            int tmp = arr[j];
 7            //注意这里不是结构上的前一个元素，而是对于组而言的，同组之间的元素交换
 8            while(j - step >= 0 && arr[j - step] > tmp){
 9                arr[j] = arr[j - step];
10                j = j - step;
11            }
12            arr[j] = tmp;
13        }
14    }
15}

希尔排序和直接插入排序的对比，对30万个随机数进行排序

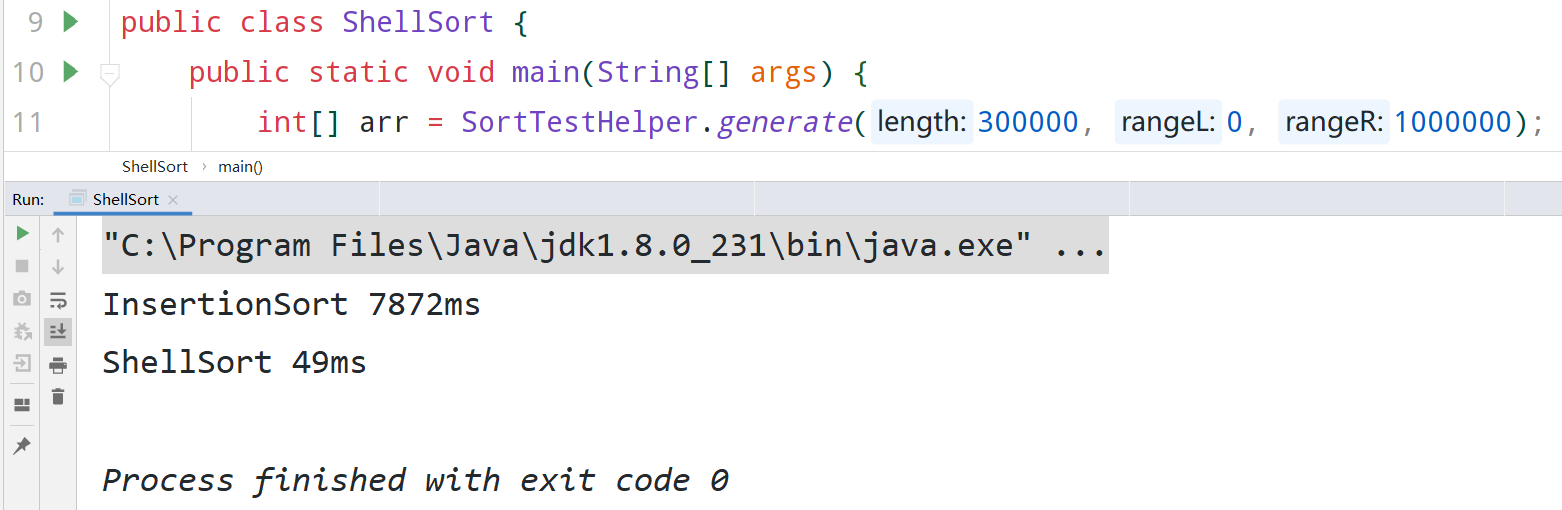
最后再思考一个问题，希尔排序是稳定排序吗？

当然不是，因为通过上面的结论我们知道，希尔排序是依靠分组来进行排序的，值相同的元素完全有可能被调换位置，所以希尔排序是一个不稳定排序。