Octave简明教程(二)
本篇文档主要内容是Octave编程中的函数定义相关内容,包括可变参数、多返回值、可变返回值等内容。以及通过Octave进行矩阵运算、求解联立方程组、计算矩阵特征值和特征向量等等。另外我会介绍Octave的高阶绘图技巧(包括绘制3D图形)。
Octave 函数
Octave 中的脚本能实现一些简单的程序,但是比脚本更加强大的是用户自定义函数。自定义函数能够让你在命令行、其他函数中和脚本中调用。在 Octave 函数中参数是通过值传递的而不是通过 reference 传递的。Octave的函数允许返回多个返回值。Octave 函数如同脚本一样,是写入一个纯文本文件中的。
无返回值的函数
不同的是函数文件的第一行遵循如下的格式,不过在命令行交互式环境,依然能够支持编写函数:
function name (arg-list)
body
endfunction
比如下面比较具体的例子:带参数的函数和不带参数的无返回值函数
octave:1> function wakeup
> printf ("hello function\n");
> endfunction
octave:2> wakeup()
hello function
# 带参数的函数
octave:3> function wakeup (message)
> printf ("this is my args: %s\n", message);
> endfunction
octave:4> what
M-files in directory /Users/zchanglin/Desktop/OctaveWK:
draw_sin_cos.m ustep.m
octave:5> wakeup('hello function with args')
this is my args: hello function with args
octave:6>
带返回值的函数
带参数的函数和不带参数的有返回值函数通常遵循如下格式:
function ret-var = name (arg-list) # 单个返回值
body
endfunction
function [ret1, ret2, ret3] = name (arg-list) # 多个返回值
body
endfunction
来看看具体的例子:
octave:1> function retval = add (a, b)
> retval = a + b;
> endfunction
octave:2> add(10,20)
ans = 30
octave:3> function [ret1,ret2,ret3] = allAddOne(a, b, c)
> ret1 = a + 1;
> ret2 = b + 1;
> ret3 = c + 1;
> endfunction;
octave:4> [r1,r2,r3] = allAddOne(10, 20, 30);
octave:5> r1
r1 = 11
octave:6> r2
r2 = 21
octave:7> r3
r3 = 31
在 Octave 中,三角函数都是使用的弧度制,但是有时候使用角度制也比较的方便。但是使用角度制的时候每次都需要使用 $sin(d/180*pi) $将角度 d 转换为弧度制并调用三角函数。但是若是使用一个函数 $sind(d)$ 会让代码更加的简单异读。那么可以创建这么一个函数,创建一个名为sind.m 的文本文件并包含以下内容:
function s=sind(x)
% SIND(x) Calculates sine(x) in degrees
s=sin(x*pi/180);
endfunction
这个函数看似简单,但是很多函数都是这样简单但是很有效。同样的,对于任意一个函数,都可以使用 help 命令阅读关于此函数的说明:
octave:1> function s=sind(x)
% SIND(x) Calculates sine(x) in degrees
s=sin(x*pi/180);
endfunction
octave:2> help sind
'sind' is a command-line function
SIND(x) Calculates sine(x) in degrees
Additional help for built-in functions and operators is
available in the online version of the manual. Use the command
'doc <topic>' to search the manual index.
Help and information about Octave is also available on the WWW
at https://www.octave.org and via the help@octave.org
mailing list.
octave:3> sind(30)
ans = 0.5000
octave:4> sind(90)
ans = 1
octave:5> sind([30 60 90])
ans =
0.5000 0.8660 1.0000
可变长度参数
如果特殊参数名称 varargin 出现在函数参数列表的末尾,则表明函数采用了可变数量的输入参数。使用 varargin 函数看起来像如下这样:
function val = smallest (varargin)
body
endfunction
varargin 的一个更复杂的示例是一个函数 print_arguments ,它打印所有输入参数:
octave:1> function print_arguments (varargin)
> for i = 1:length (varargin)
> printf ("Input argument %d: ", i);
> disp (varargin{i});
> endfor
> endfunction
octave:2> print_arguments(1, 5, "Tim")
Input argument 1: 1
Input argument 2: 5
Input argument 3: Tim
octave:3>
可变长度返回值
可以使用类似于特殊 varargin 参数名称的语法从函数返回可变数量的输出参数。为了让函数返回可变数量的输出参数,使用了特殊的输出参数名称 varargout 。与 varargin 一样, varargout 是一个单元格数组,其中将包含请求的输出参数。
比如下面这个例子,此函数将第一个输出参数设置为1,第二个设置为2,以此类推,返回值随参数列表变化:
octave:1> function varargout = one_to_n ()
for i = 1:nargout
varargout{i} = i;
endfor
endfunction
octave:2> [a, b, c, d] = one_to_n()
a = 1
b = 2
c = 3
d = 4
octave:3>
参数/返回值有效性校验
Octave是一种弱类型的编程语言。因此有可能调用一个带有参数的函数,而这些参数可能会导致错误或产生不良的副作用。例如:调用一个带有巨大稀疏矩阵的字符串处理函数。
在函数的头部验证它是否被正确调用是一个很好的做法,Octave 提供了几个用于此目的的函数,不过在看校验函数的使用之前先看看自己如何手动校验的:
octave:1> function ret = add(x)
% Compute the sum of all the elements of the vector
tmp = 0;
m = length(x);
if(m < 2)
error("args nums error, must >= 2")
endif
for n=1:m
tmp = tmp + x(n);
endfor
ret = tmp;
endfunction
octave:2> add([0])
error: args nums error, must >= 2
error: called from
add at line 5 column 9
octave:3> add([0 3 4 5])
ans = 12
narginchk 和 nargoutchk 函数提供了类似的错误检查。narginchk(minargs, maxargs) 检查输入参数的数量是否正确,如果调用函数中的参数数量超出 minargs 和 maxargs 范围,则生成错误消息。否则就什么都不做,对于 nargoutchk 也是如此,不过它是用来校验返回值的。
minargs 和 maxargs 必须是标量数值。零、无穷大和负值都是允许的,并且 minargs 和 maxargs 可以相等。
校验参数
octave:1> function print_arguments (varargin)
narginchk(1, 3)
for i = 1:length (varargin)
printf ("Input argument %d: ", i);
disp (varargin{i});
endfor
endfunction
octave:2> print_arguments(2,3,4,5)
error: narginchk: too many input arguments
error: called from
narginchk at line 60 column 5
print_arguments at line 2 column 1
octave:3> print_arguments(2,3)
Input argument 1: 2
Input argument 2: 3
octave:7>
校验返回值
octave:1> function varargout = one_to_n ()
nargoutchk(1, 3)
for i = 1:nargout
varargout{i} = i;
endfor
endfunction
octave:2> [a b c d] = one_to_n()
error: nargoutchk: Too many output arguments.
error: called from
nargoutchk at line 102 column 7
one_to_n at line 2 column 3
octave:3> [a, b, c] = one_to_n()
a = 1
b = 2
c = 3
octave:4>
加载函数操作路径
调用函数时,Octave 会在目录列表中搜索包含函数声明的文件。其实仍然是工作空间的概念,默认情况下会从 Octave 分发的目录列表以及当前工作目录加载所有的函数。addpath 函数可以向加载路径添加目录,rmpath 命令会从加载路径中删除目录,这一点与Script模式一样。
矩阵与向量运算
矩阵乘法
矩阵乘法必需满足一定的矩阵大小规则,在矩阵乘法中,矩阵大小为: $$ (l \times m) *(m \times n) \rightarrow(l \times n) $$ 方阵还可以使用矩阵乘方计算:
octave:1> A=[1 2; 2 1] # 定义矩阵
A =
1 2
2 1
octave:2> A * A # 矩阵乘法
ans =
5 4
4 5
octave:3> A.^2 # 元素逐个2次方
ans =
1 4
4 1
octave:4> A.*A # 元素逐个相乘
ans =
1 4
4 1
octave:15>
矩阵转置
矩阵转置运算,将其由行向量转为列向量或者由列向量转换为行向量:
octave:1> A = rand(2,3) # 生成随机2 * 3的矩阵
A =
0.3702 0.1428 0.9297
0.3102 0.1288 0.5229
octave:2> A'
ans =
0.3702 0.3102
0.1428 0.1288
0.9297 0.5229
矩阵创建
之前我们已经知道了 ones 和 zeros 这两个创建全 1 或者 全 0 的矩阵,现在来看看其他的矩阵创建函数,Octave 中使用 eye 矩阵来创建单位矩阵:
octave:1> eye(3)
ans =
Diagonal Matrix
1 0 0
0 1 0
0 0 1
单位矩阵是对角矩阵的特殊情况,Octave 提供了 diag 函数来创建这样的矩阵,输入参数为该对角矩阵的对角元向量即可得到对应的对角矩阵。该函数如果传入已经存在的对角矩阵,返回对角元素:
octave:1> diag([2 4 6 6])
ans =
Diagonal Matrix
2 0 0 0
0 4 0 0
0 0 6 0
0 0 0 6
octave:2> A = diag(A)
A =
2
4
6
6
octave:3>
如果需要创建一个空矩阵来向其中添加矩阵元。定义这样的矩阵用方括号实现,比如:E = []
如果你需要用一些小矩阵来创建一个复合矩阵,这在 Octave 中也很简单,但是需要注意子矩阵的行列数的匹配:
octave:1> A=[5 2 2; 0 8 9];
octave:2> B=[2 0;0 -1;1 0];
octave:3> comp=[eye(3) B; A zeros(2,2)]
comp =
1 0 0 2 0
0 1 0 0 -1
0 0 1 1 0
5 2 2 0 0
0 8 9 0 0
octave:4>
提取矩阵元
引用矩阵中的元素与向量中的操作一样,使用括号 () 即可。所以对于矩阵,需要指定其行号和列号:
octave:5> A = [1 2 3; 4 5 6; 7 8 9];
octave:6> A(1,1)
ans = 1
octave:7> A(2,3)
ans = 6
octave:8> A(3,1)
ans = 7
octave:9>
冒号表达式在其中依然适用,其中冒号用来指定元素的的范围,单独使用该符号表示整行或者整列。
......
comp =
1 0 0 2 0
0 1 0 0 -1
0 0 1 1 0
5 2 2 0 0
0 8 9 0 0
octave:3> A = [1 2 3; 4 5 6; 7 8 9];
octave:4> A(3, :)
ans =
7 8 9
octave:5> comp(4, 3:5)
ans =
2 0 0
octave:6>
矩阵常用函数
| 函数 | 描述 |
|---|---|
| eye | 创建一个单位矩阵 |
| zeros | 创建一个全0矩阵 |
| ones | 创建一个全1矩阵 |
| rand | 创建一个随机矩阵 |
| diag | 创建一个对角矩阵,或者提取一个矩阵的对角元 |
| inv | 求矩阵的逆矩阵 |
| det | 求矩阵特征值 |
| trace | 求矩阵的迹 |
| eig | 求矩阵的特征向量和特征值 |
| rank | 求矩阵的秩 |
| null | 计算矩阵的零空间的一组基 |
| rref | 增广矩阵进行高斯消元法 |
| lu | 计算矩阵LU分解 |
| qr | 计算矩阵QR分解 |
| svd | 计算矩阵的奇异值分解 |
| pinv | 计算矩阵的虚反矩阵 |
下面是一些使用示例:
octave:14> A = rand(4,4)
A =
0.710311 0.930717 0.972224 0.507164
0.073195 0.358159 0.669564 0.769522
0.258537 0.853792 0.718105 0.450334
0.423404 0.290824 0.749534 0.022108
octave:16> eig(A)
ans =
2.1140 + 0i
0.2524 + 0i
-0.2789 + 0.3201i
-0.2789 - 0.3201i
octave:17> rank(A)
ans = 4
octave:18> inv(A)
ans =
3.0323 -0.2937 -2.8678 -0.9233
-0.1606 -1.0876 2.0792 -0.8121
-1.6876 0.5479 0.8557 2.2139
1.2547 1.3569 -1.4395 -1.4605
octave:19> rref(A)
ans =
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
octave:20> lu(A)
ans =
0.7103 0.9307 0.9722 0.5072
0.3640 0.5150 0.3642 0.2657
0.1030 0.5092 0.3839 0.5819
0.5961 -0.5125 0.9291 -0.6847
octave:21>
Octave绘图进阶
Octave 的画图功能不仅仅是画简单的二维直角坐标系下的曲线。通过调用 GNUPLOT,它可以画出条形图,3D 表面,等高线图和极坐标图等等。有关这些内容的细节可以参考 Octave 的帮助系统或者官方文档。
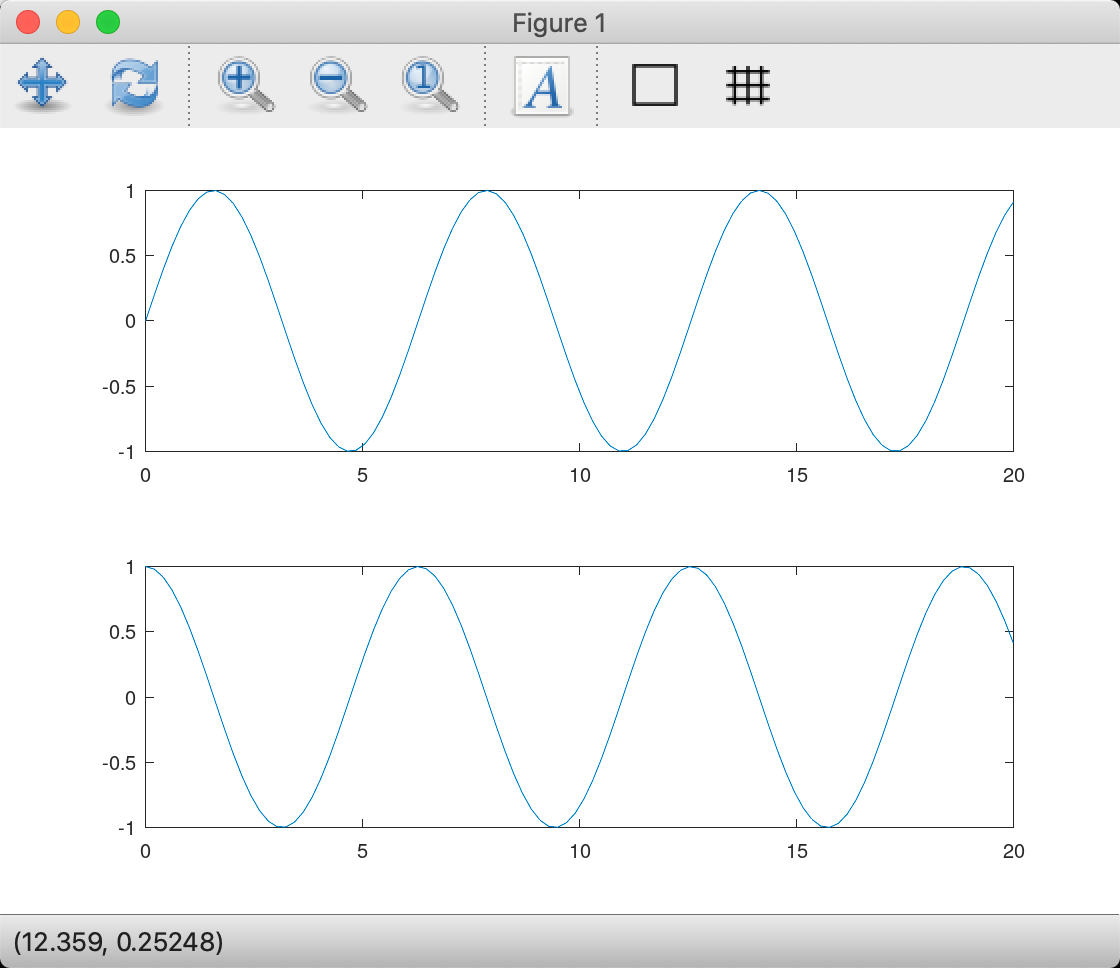
子图(窗口多个图像)
要在同一个窗口中创建多幅图片通过 subplot 命令实现。该命令能够将窗口分离成一系列的子窗口,其基本语法为 subplot(row, columns, select),其中 select 参数指定当前绘图在子窗口中的序列。子窗口的序号按照从上到下,从左到右的次序递增。接下来用一个例子来说明 subplot 的应用:
octave:1> x = linspace(0, 20);
octave:2> subplot(2, 1, 1)
octave:3> plot(x, sin(x));
octave:4> subplot(2, 1, 2)
octave:5> plot(x, cos(x));
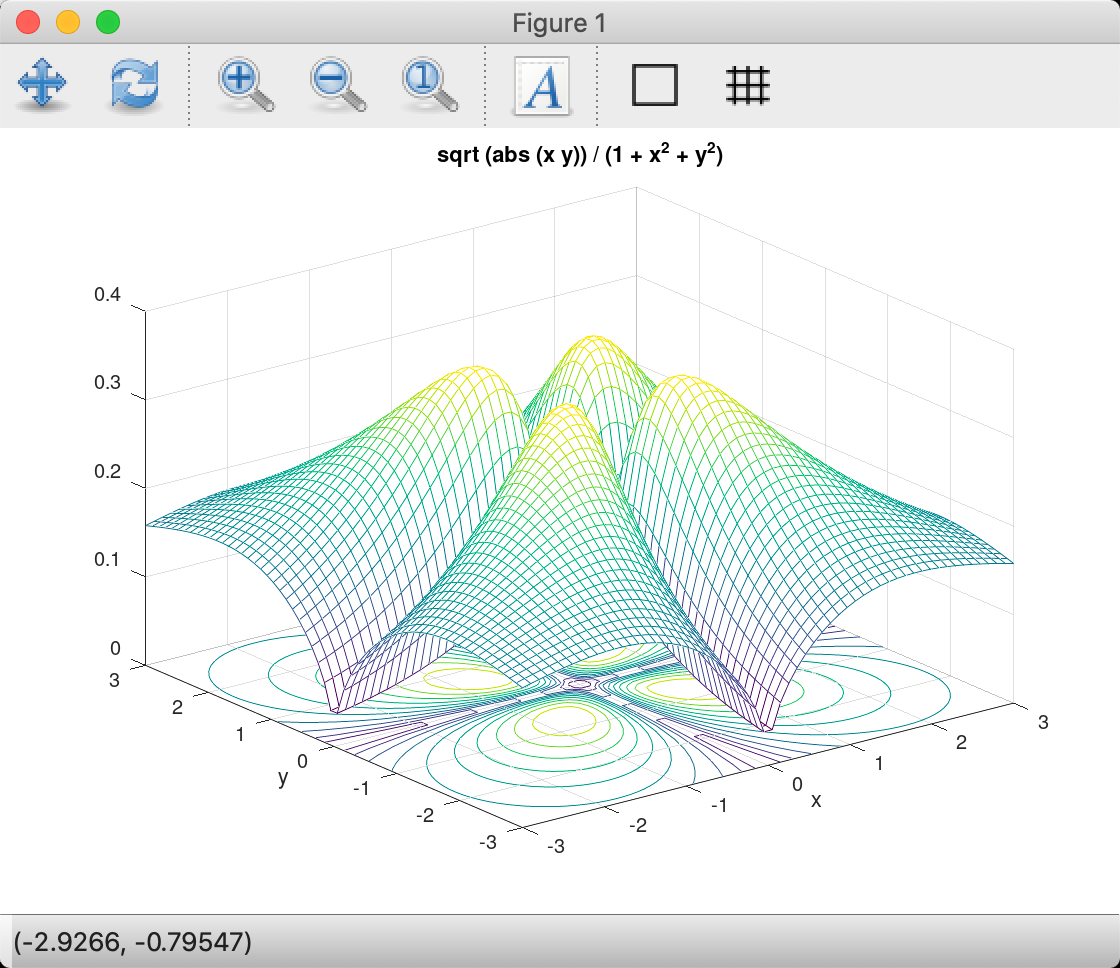
3D绘图
Octave 同样提供了多样的 3D 数据可视化工具。最简单的 3D 绘图实现是 plot3 命令。该命令通过接受输入的 x, y 和 z 轴的数据,绘制绘制函数定义的网格线和等高线,使用参数式的函数:
octave:1> f = @(x,y) sqrt (abs (x .* y)) ./ (1 + x.^2 + y.^2);
octave:2> ezmeshc (f, [-3, 3])
在 3D 绘图中 xlabel 和 ylabel 照常使用,而新的 zlabel 命令可以为 z 轴命名。 而且在绘制 3D 图时,线条的样式选项也可以使用,这个在之前的2D绘图中有说到,使用鼠标拖动即可选择合适的视角。
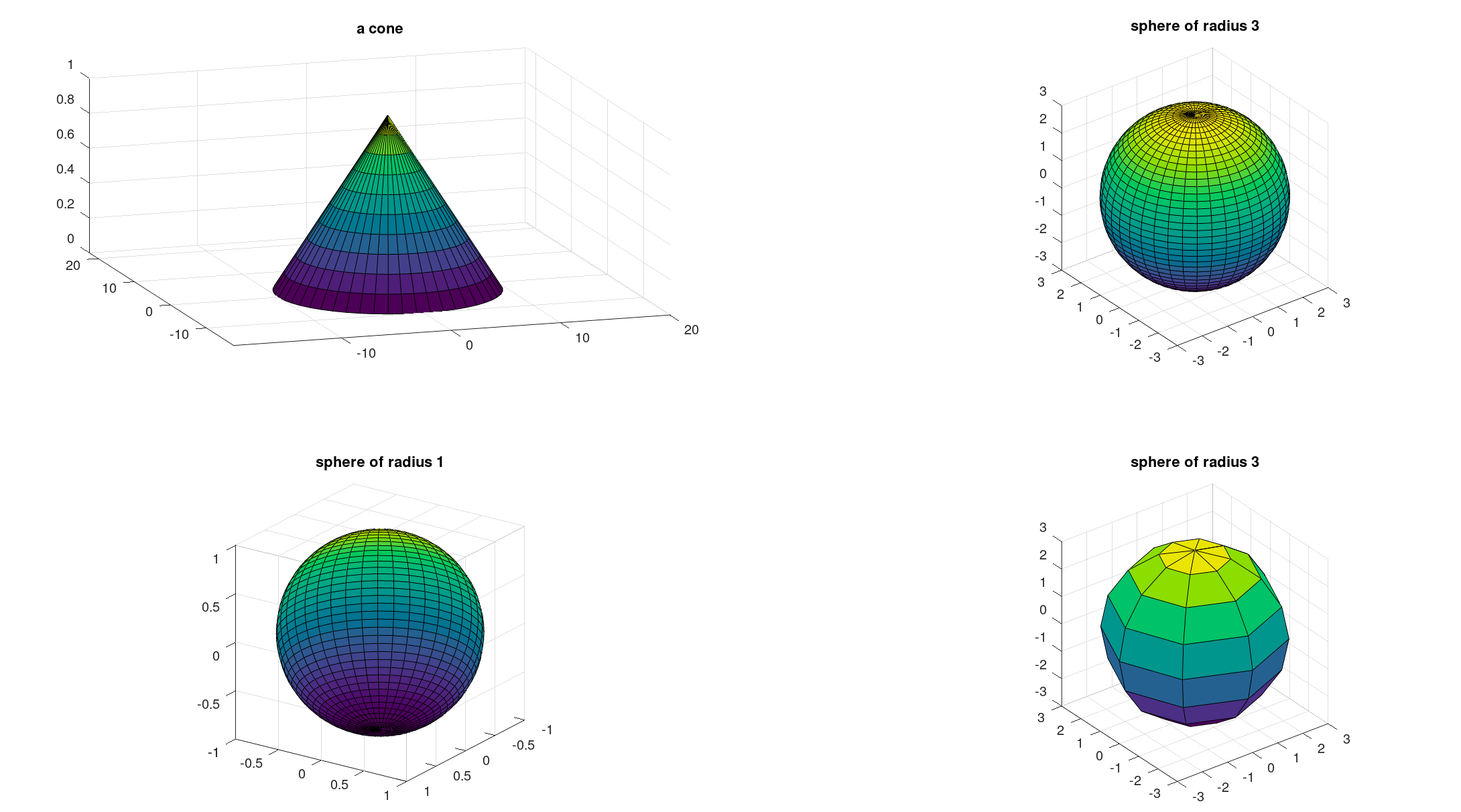
绘制形状
Octave提供了非常多的函数来绘制三维几何形状,球体、圆柱体等都有对应的函数,查阅相关文档即可搞清楚函数的使用方式,比如绘制球体和圆锥:
octave:1> subplot(2, 2, 1)
octave:2> [x, y, z] = cylinder (10:-1:0, 50);
surf (x, y, z);
title ("a cone");
octave:3> subplot(2, 2, 2)
octave:4> [x, y, z] = sphere (40);
surf (3*x, 3*y, 3*z);
axis equal;
title ("sphere of radius 3");
octave:5> subplot(2, 2, 3)
octave:6> [x, y, z] = sphere (40);
surf (1*x, 1*y, 1*z);
axis equal;
title ("sphere of radius 1");
octave:7> subplot(2, 2, 4)
octave:8> [x, y, z] = sphere (8);
surf (3*x, 3*y, 3*z);
axis equal;
title ("sphere of radius 3");
octave:9>
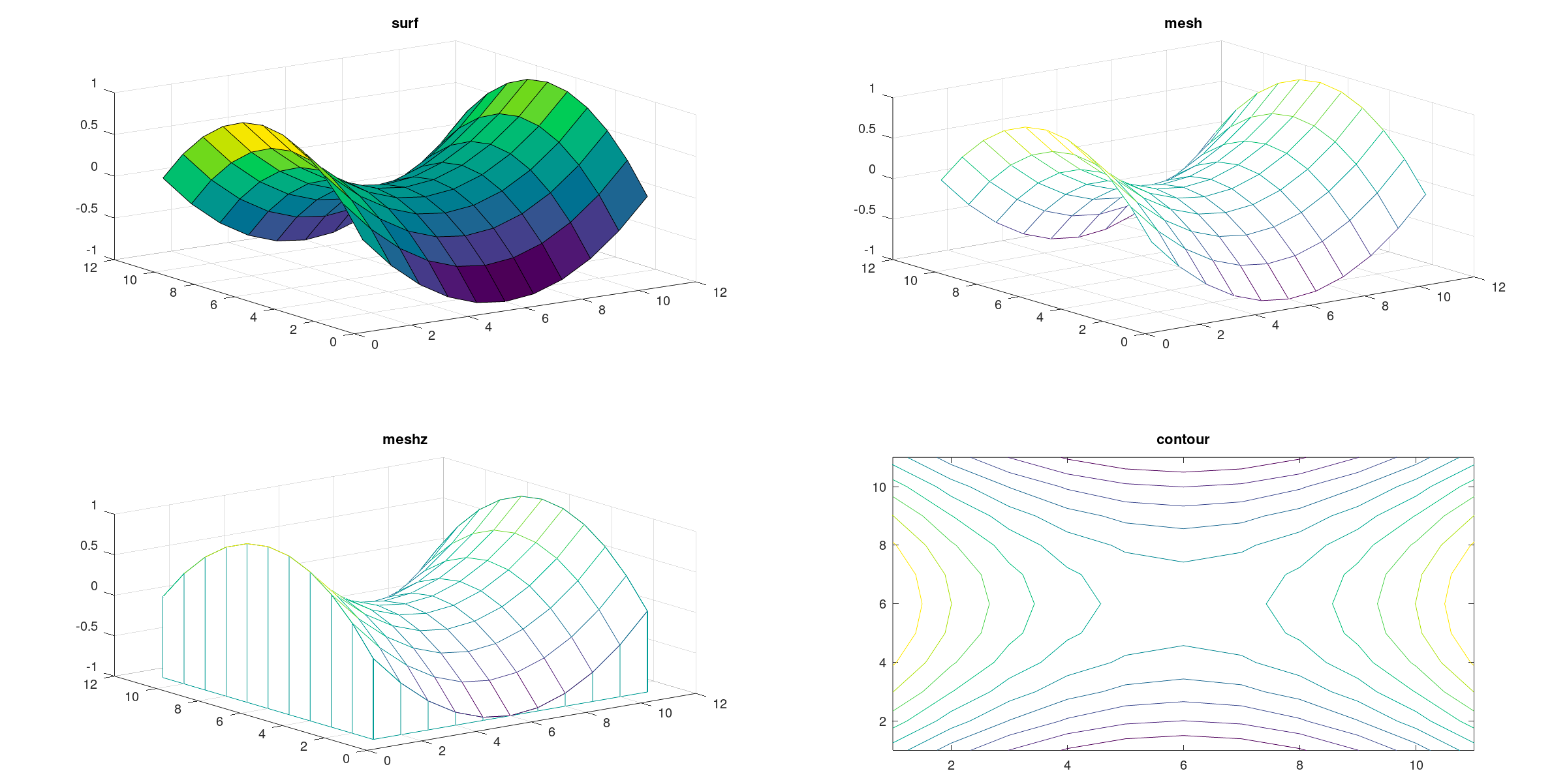
绘制曲面
定义一个二元函数 $f(x, y)$,该函数的曲面可以用一系列的 Octave 的工具画出。首先,要初始化一个网格点,用 meshgird 命令实现。
octave:1> x=2:0.2:4;
octave:2> y=1:0.2:3;
octave:3> [X,Y]=meshgrid(x,y);
octave:4> Z=(X-3).^2-(Y-2).^2;
octave:5> subplot(2, 2, 1);
octave:6> surf(Z);title('surf')
octave:7> subplot(2, 2, 2)
octave:8> mesh(Z);title('mesh')
octave:9> subplot(2, 2, 3)
octave:10> meshz(Z);title('meshz')
octave:11> subplot(2, 2, 4)
octave:12> contour(Z);title('contour')
参考资料
Octive官方文档 https://octave.org/doc/v6.4.0/