Tim's Note

ESP8266-NodeMCU是一个开源硬件开发板，由于它支持WIFI功能，所以在IOT领域，Arduino开发板最大的对手之一就是ESP8266-NodeMCU开发板。ESP8266-NodeMCU尺寸与Nano类似，他并不是Arduino团队开发的，但是我们也可以使用Arduino IDE 对其进行开发，NodeMCU是以ESP8266芯片为核心的开发板，无论是芯片价格还是开发板的价格都是比较实惠的，总体来说ESP8266作为IOT的接入设备是非常划算的。

通过OpenGL渲染摄像头数据到屏幕时，使用GLSurfaceView就可以完成，如果要做中间层处理，比如美颜等，通过着色器处理之后写入帧缓冲(FBO)来完成的。那么如何从着色器拿到数据然后编码生成视频呢？一般来说，使用软编码或者MediaCodec来进行编码，如果图像的byte[] 拿到了，编码就简单了，但是现在时在着色器中处理的，没有byte[]，怎么将我们处理之后的图像变成一个Mp4文件呢？

本篇文章主要是介绍离屏渲染与OpenGL的帧缓冲， 当有些图像不能直接绘制于屏幕上，需要在别的地方做额外的处理预合成，就使用到离屏渲染。所以其实离屏渲染的概念很简单，就是在某块内存中处理图像，经过层层处理，最终效果显示到屏幕上而已。而OpenGL提供了帧缓冲对象 (Frame Buffer Object, FBO)，借助FBO很容易实现离屏渲染。

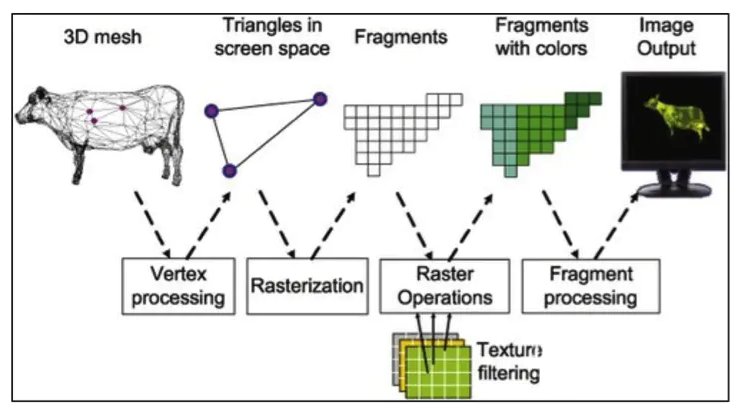
Graphics Pipeline 实际上指的是一堆原始图形数据途经一个输送管道，期间经过各种变化处理最终出现在屏幕的过程。图形渲染管线可以被划分为两个主要部分：第一部分把你的3D坐标转换为2D坐标，第二部分是把2D坐标转变为实际的有颜色的像素。下面来看看OpenGL渲染管线的主要流程吧！

OpenGL（Open Graphics Library）定义了一个跨编程语言、跨平台编程的专业图形程序接口规范，所以说OpenGL只是一套规范，不要理解成FFmpeg那种开源库了。本篇文章会涉及OpenGL的着色语言GLSL，以及如何使用OpenGL来渲染摄像头图像到屏幕上，并且通过着色器可以实现灰度化，底片等效果。

前段时间学习了ESP8266的AT指令集，现在通过AT指令初始化ESP8266+串口通信的方式，完成WLAN下的信息交换，比如手机、PC、其他MCU与STC89 C51的通信等等。其中踩了不少的坑，特此记录一下。ESP8266小模块系列常见的就下面几种：ESP-01S比ESP-01多了两颗小料并增强了天线的强度，其他的是一样的，完全通用！

本篇文章主要是三个部分，刷入官方原厂固件，进入透传模式，常用的AT指令集。有时候控制端不需要MCU反馈信息，那么就可以使用透传模式进行控制。USB转ESP8266通常再买回来的时候就已经刷入了官方固件，但是如果自己要重新刷入就需要USB转TTL，所以最好一次买两个USB-TTL，一个焊接好作为烧录器，另一个日常使用是比较方便的。

纠错码(error correcting code)，在传输过程中发生错误后能在收端自行发现或纠正的码。

仅用来发现错误的码一般常称为检错码。

为使一种码具有检错或纠错能力，须对原码字增加多余的码元，以扩大码字之间的差别 ，即把原码字按某种规则变成有一定剩余度（见信源编码）的码字，并使每个码字的码之间有一定的关系。关系的建立称为编码。码字到达收端后，可以根据编码规则是否满足以判定有无错误。当不能满足时，按一定规则确定错误所在位置并予以纠正。纠错并恢复原码字的过程称为译码。检错码与其他手段结合使用，可以纠错。