Kibana 是为Elasticsearch设计的开源分析和可视化平台，利用Kibana可以很容易对Elasticsearch中的数据实现图表可视化、搜索等功能。当然熟悉Kibana的前提是对Elasticsearch有一定的了解，这是kibana的官方手册： https://www.elastic.co/guide/cn/kibana/current/d4c0f50720a538647399fc1363896cce.html ，本篇文章主要是Lucene查询语法，添加索引，以及如何使用Kibana的可视化平台（图表和仪表盘）。
本篇文章主要学习 Flink的核心API的基础部分的笔记， 在学习之前先部署了一个单节点的Flink环境，然后重点需要了解的就是Flink的执行上下文(StreamExecutionEnvironment)、数据源(Source API)、转化相关操作(Transformation)、输出(Sink) 等，另外就是提交和取消作业的一些操作。
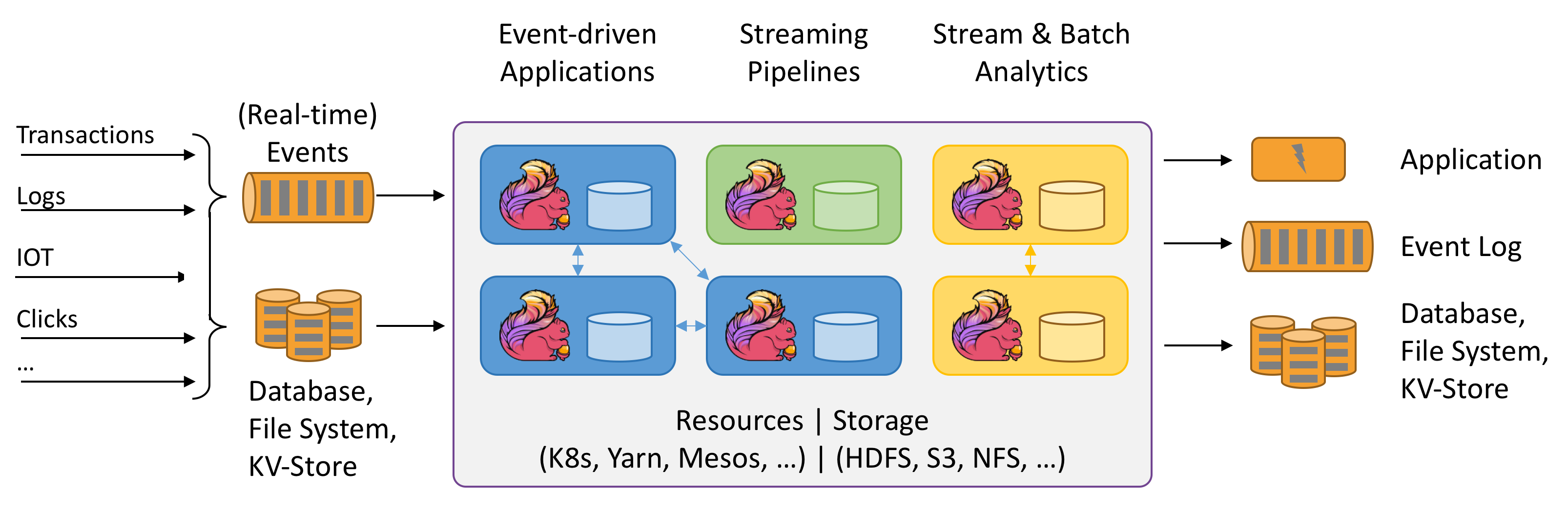
也是因为最近处理业务上的问题，如果我希望看到某些实时数据的变化那么必然会涉及到流式计算，大数据处理框架从原始的 MapReduce、Hive 到 DAG的Tez，再到Spark的近实时处理是一个不断进化的过程，对于要求更高的场景还是Apache Flink比较在行，Apache Flink是一个带状态的流式计算框架，Flink不但能进行流式计算，也能进行批处理，也就是离线计算。下面是最近两天学习Flink的一些笔记，后面会逐步完善和校正。
最近在B站开了一个Unix系统编程的系列分享，目前打算是一周至少出2期视频，不过于追求速度但求精细，对于涉及操作系统原理部分肯定也会深入讲解，同时也是自己巩固知识的最好方法。买了《UNIX环境高级编程》（第三版）这本书但是一直没看，自己对Linux系统编程除了上大学的时候写的一些Demo以外就没写过其他东西了，但是NDK开发中时不时还会用到，而且一旦涉及内存优化、OOM监控这些必定跟Linux底层脱不了干系，所以花一些时间巩固基础，同时也保持一颗分享的初心，通过简单明了通俗易懂的方式给大家呈现出来。绝不同于部分大学课堂的只念PPT，更注重实际操作，通过实操加深对知识的理解，本节是 Vim 的常用操作和一些配置，放在博客里仅供参考，Bilibili合集的地址是： https://www.bilibili.com/video/BV1ua411b7sF
一元线性回归算法是机器学习部分接触的第一个算法，更重要的通过一元线性回归足以了解监督学习过程完整的流程，之所以称为监督学习是因为对于每个数据来说，已经存在了正确的答案。本文所有的内容都只是在学习Andrew Ng老师的机器学习课程中记的笔记，并且自己用Ocatve实现了一元线性回归的梯度下降算法。
本篇文档主要内容是Octave编程中的函数定义相关内容，包括可变参数、多返回值、可变返回值等内容。以及通过Octave进行矩阵运算、求解联立方程组、计算矩阵特征值和特征向量等等。另外我会介绍Octave的高阶绘图技巧（包括绘制3D图形）。
GNU Octave是一种以高级编程语言为特色的软件，主要用于数值计算和绘图。通过Octave可以非常方便的进行矩阵运算、求解联立方程组、计算矩阵特征值和特征向量等。本篇文档主要内容是Octave基础命令、数据格式、绘制图形、Octave脚本编写、Octave函数编程等内容。另外，此文档会不断补充常见使用场景。
证明的过程非常简单，那就是如何通过积分的思想来证明圆的面积公式。不过与其这样表达倒不如说是通过圆的面积公式来体会体会积分的思想。首先把整个圆看成是无数个同心圆环组成的图形，只要把每个圆环的面积相加，就会得到最终的面积。